8. Odrezané dážďovky vzorové riešenie

1234

4

4321

2

11131719

6

Táto úloha bola dosť o premýšľaní a to bolo na nej super. Navyše, málokedy sa nám v KSP podarí taká pekná úloha s množstvom rôznych možných prístupov od nesprávnych riešení po správne riešenia so zložitosťami od \(O(2^n)\) cez \(O(n^3)\), \(O(n^2)\), \(O(n\sqrt{n})\), \(O(n^{1.25})\), \(O(n \log{n})\) až po \(O(n)\). Premennou \(n\) označujeme v celom vzorovom riešení dĺžku vstupu (dĺžku dážďovky). Všetky tieto riešenia so sebou nesú nejaké ponaučenie, tak vám odporúčame pozorne čítať. Text je možno trochu dlhší, pretože sa snažíme poriadne vysvetliť všetky detaily. Nemusíte ho celý čítať naraz.

Medzi nesprávne riešenia patrí množstvo pažravých prístupov, napríklad idem od začiatku dážďovky a vždy useknem čo najkratší kus, aby som ich mal na konci čo najviac. Protipríkladom je napríklad postupnosť 54638291 ktorú by sme pažravo nasekali 5,46,38291 a správne je 54,63,82,91. Pažravé riešenia v tejto úlohe nefungujú.

Pomalé riešenie \(O(n^2)\)

Určite by ste všetci zvládli naprogramovať riešenie, ktoré rekurzívne skúša všetky možnosti. V tomto rekurzívnom riešení sa dookola pýtame takéto otázky: Na koľko najviac kusov môžeme nasekať prvých \(i\)-cifier vstupu, ak posledný kus má \(j\)-cifier? Pričom riešenie úlohy je maximum pre všetky možné \(j\) a pre \(i=n\). Odpoveď na takúto otázku si označíme P[i][j] a vieme ju ľahko spočítať z iných hodnôt \(P\), pre iné \(i\) a \(j\). P[i][j] je maximum z P[i-j][k]+1 pre všetky \(k \geq 1\) také, že posledný kus kratšej dážďovky je menší ako posledný kus dlhšej. Očividne môžeme použiť všetky \(k\le j\), pretože menejciferné číslo je istotne menšie ako viacciferné. A to, či môžeme uvažovať aj hodnotu P[i-j][j] zistíme porovnaním dvoch reťazcov dĺžky \(j\).

Inak povedané, hodnotu P[i][j] vieme zistiť v čase \(O(j)\)¹, na základe iných hodnôt P. A takto vieme spočítať všetky P pre všetky \(1\leq j\leq i\leq n\), čo je \(O(n^2)\) možností. Naťukáme túto myšlienku do počítača a dostaneme riešenie so zložitosťou \(O(n^3)\).

Ha! S minimálnou úpravou kódu vieme dostať riešenie so zložitosťou \(O(n^2)\). Stačí uvažovať také sekania, kde dĺžka každého kusu dážďovky bude \(O(\sqrt{n})\), presnejšie \(j\leq \sqrt{2n}+1\) (čoskoro si povieme, prečo to stačí) Potom zložitosť tohto riešenia je \(O(n \sqrt{n} \sqrt{n}) = O(n^2)\).

#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
#include<cmath>
using namespace std;
#define NEDASA -47

string dazdovka; // vstup
vector<vector<int> > P; // pocet kusov do pozicie i, ak posledny kus bol dlhy j

// porovnaj cisla, ktore maju 'dlzka' cifier a zacinaju na poziciach i1, i2
bool mensie(int i1, int i2, int dlzka) {
    for(int i = 0; i < dlzka; ++i) 
        if (dazdovka[i1+i] != dazdovka[i2+i])
            return dazdovka[i1+i] < dazdovka[i2+i];
    return false;
}

// rekurzivne spocitame P[i][j]
int pocet(int i, int j) {
    if (i == j) return 1;
    if (i < j) return NEDASA;
    // ak sme uz odpoved spocitali, nebudeme pocitat znova
    if (P[i][j] != -1) return P[i][j];
    
    int najlepsie = NEDASA;
    for(int k = 1; k<j; k++)
        najlepsie = max(najlepsie, pocet(i-j, k)+1);
    if (i>=2*j && !mensie(i-j, i-2*j, j))
        najlepsie = max(najlepsie, pocet(i-j, j)+1);

    if (najlepsie < 0) najlepsie = NEDASA;
    return P[i][j] = najlepsie;
}

int main() {
    cin >> dazdovka;
    int n = dazdovka.size();
    int odmocnina = sqrt(2*n)+2;
    P = vector<vector<int> > (n+1, vector<int>(odmocnina+1, -1));
    int najlepsie = 0;
    for(int j = 1; j < odmocnina; ++j)
        najlepsie = max(najlepsie, pocet(n, j));
    cout << najlepsie << endl;
}

Príprava na rýchlejšie riešenie

Na rýchlejšie riešenia ako \(O(n^2)\) si potrebujeme spraviť to sľubované premýšľanie. Ukážeme si, že stačí uvažovať len niektoré sekania dážďovky.

Mimochodom, dĺžkou kusu/čísla rozumieme počet jeho cifier. Často budeme využívať fakt, že ak číslo \(B\) je dlhšie ako \(A\), tak \(B\) je určite väčšie.

Pozorovanie 1.

Stačí nám uvažovať také riešenia, kde sa dĺžky susedných kusov dážďovky líšia najviac o 2.

Ak by sa totiž niektoré dva susedné kusy \(A,B\) líšili o 3 alebo viac, môžeme ľavý kus \(A\) predĺžiť o 1 a pravý kus \(B\) skrátiť o 1. Tým pádom všetky ostatné kusy ostanú nezmenené a určite sme nespôsobili žiadny problém pri porovnaniach ktorýchkoľvek z kusov. Číslo \(A\) je naďalej väčšie od kusov naľavo, pretože už predtým bolo väčšie a teraz sme ho len zväčšili. Podobne \(B\) je menšie od kusov napravo. Napokon \(A\) je menšie ako \(B\), pretože \(B\) má aspoň o jednu cifru viac. Opakovaním takýchto posunov o 1 dosiahneme, že rozdiely dĺžok sú všade najviac dva.

Podobne, nikdy v optimálnom riešení nebude prvý úsek dlhší ako dve cifry, pretože ak by mal viac ako dve cifry, tak ho určite môžeme rozdeliť na prvú cifru a zvyšok, čím dostaneme lepšie riešenie.

Teraz vieme spraviť prvý odhad na dĺžku kusov. Keďže prvý kus je dlhý najviac dva a každý ďalší môže byť najviac o dva dlhší, najväčšie možné dĺžky dosiahneme, ak budú postupne počty cifier v úsekoch \(2,4,6,8,10,12,...,2k\).

Celková dĺžka dážďovky potom bude \(k(k+1)\). Opačne, ak vieme, že dĺžka dážďovky je \(n\), tak \(k < \sqrt{n}\) a dĺžka najväčšieho úseku v nejakom optimálnom riešení bude najviac \(2\sqrt{n}\). Neskôr si ukážeme, že je to dokonca najviac \(\sqrt{2n}+1\).

Zároveň ľahko nájdeme vstupy, kde v optimálnom riešení má najväčšie číslo viac ako \(\sqrt{2n}-1\) cifier, takže tento odhad už sa veľmi nedá zlepšiť.

Pozorovanie 2.

V skutočnosti nemusíme hľadať čo najvyšší počet kusov dážďovky, ako nabáda zadanie, ale môžeme nájsť také nasekanie, aby posledný kus bol čo najmenší. Je to totiž takmer to isté.

Kľúčovým pozorovaním tejto úlohy je to, že nám stačí uvažovať len také riešenia, ktoré končia najmenším možným číslom, resp. najkratším možným kusom². Predstavme si, že sme nasekali dážďovku tak, aby bol posledný kus čo najkratší. Nech má posledný kus dĺžku \(m\). Zároveň spomedzi všetkých nasekaní, ktoré majú posledný kus dlhý \(m\) vyberieme to, ktoré má najväčší počet kusov. Toto nasekanie volajme \(A\) a označíme si jednotlivé pozície rezov \(i_1, i_2, i_3,\dots , i_k\).

Čo by sa stalo, keby toto nasekanie nebolo optimálne z hľadiska počtu kusov? Ak sa nám podarí prísť ku sporu, zistíme, prečo toto nasekanie muselo byť optimálne.

Pre spor teda predpokladajme, že existuje iné nasekanie \(B\) na pozíciách \(j_1, j_2,\dots ,j_{k+1}\), ktoré má viac kusov. Z predpokladov vieme, že posledný kus \(B\) je dlhší ako posledný kus \(A\), preto \(j_{k+1} < i_{k}\). Navyše si označme myslený nultý rez úplne na začiatku dážďoviek \(i_0 = j_0 = 0\).

Pozrime sa na najmenšiu dvojicu indexov \((a,b)\), pre ktoré platí, že \(1\leq a \le b \leq k+1\) a zároveň \(i_a > j_b\). (Pri výbere najmenšej najprv zoraďujeme podľa a, potom podľa b.) Keďže existuje aspoň jedna taká dvojica (k, k+1) a možných dvojíc je konečne veľa, tak určite existuje najmenšia.

Vieme tiež, že \(i_{a-1}\leq j_{b-1}\), inak by \((a,b)\) nebola najmenšia dobrá dvojica. Taktiež \(j_{b-1} < i_a\), pretože \(i_b < i_a\).

No ale potom vieme vyrobiť nové nasekanie \(C\), ktoré bude pozostávať z rezov \(j_1 \dots j_{b-1}\) a rezov \(i_a \dots i_k\). O tomto nasekaní vieme povedať, že

• Je korektné a spĺňa nerovnosti so zadania. Totiž, číslo pozostávajúce z cifier medzi rezmi \(j_{b-1}\) a \(i_a\) je väčšie ako číslo medzi rezmi \(j_{b-1}\) a \(j_b\) a preto je aj väčšie od čísla pred ním. Taktiež je toto číslo menšie alebo rovné od čísla medzi rezmi \(i_{a-1}\) a \(i_a\) a tým pádom aj menšie ako číslo za ním. Všetky ostatné nerovnosti platia, pretože platili v pôvodných dážďovkách.
• Má \(k+1\) kusov, čiže je dlhšie ako nasekanie \(A\).
• Končí rovnakým číslom ako nasekanie \(A\).

A to je spor s tým ako sme vybrali nasekanie \(A\). \(\square\)

Ukázali sme, že nasekanie \(A\) je optimálne, pretože ak by existovalo nasekanie s väčším počtom kusov, dostali by sme sa do sporu. Pre lepšiu predstavu si pozrite ilustračný obrázok ku dôkazu.

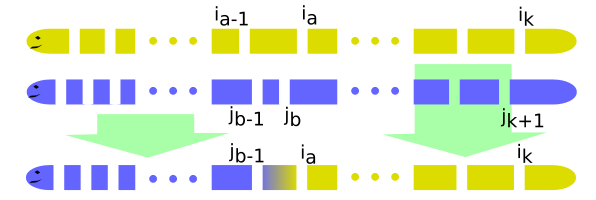
Dôsledky

Vďaka druhému pozorovaniu, vieme, že nasledujúci algoritmus funguje správne. Spočítame, akým najkratším kusom vieme ukončiť nasekanie dážďovky. Odsekneme ten najkratší možný kus. Opakujeme postup s kratšou dážďovkou.

Druhý dôsledok je tesnejší odhad pre počet cifier všetkých čísel. Keby mali jednotlivé kusy dĺžky postupne \(1,2,3,4,\dots\) prípadne s jedným vynechaným číslom aby to pasovalo na dĺžku dážďovky, tak dostaneme riešenie, ktoré končí číslom kratším ako \(\sqrt{2n}+1\). Tým pádom riešenie, ktoré končí najkratším možným kusom, končí tiež kusom kratším ako \(\sqrt{2n}+1\). A tým pádom existuje aj optimálne riešenie s kratším kusom na konci. A keďže posledný kus je zo všetkých najdlhší, tak sme dostali horný odhad na dĺžku všetkých kusov.

Tretí dôsledok je rýchlejšie riešenie úlohy.

Rýchlejšie riešenie – \(O(n \sqrt {n})\)

Pamätáte si ešte pôvodné rekurzívne riešenie, kde sme sa snažili pre každé \(i,j\) zistiť, na koľko najviac kusov môžeme nasekať prvých \(i\)-cifier vstupu, ak posledný kus má \(j\)-cifier? Tak teraz už vieme, že nemusíme rozlišovať, koľko cifier má posledný kus – stačí uvažovať rozsekanie s najkratším možným koncom.

Takže po novom už budeme počítať \(P[i]\) – na koľko najviac kusov môžeme nasekať prvých \(i\) cifier dážďovky a \(D[i]\), koľko najmenej cifier môže mať posledný kus.

Celková zložitosť algoritmu bude \(O(n\sqrt{n})\), pretože každé \(P[i]\) a \(D[i]\) spočítame v čase \(O(D[i])\) z týchto hodnôt pre menšie \(i\). Najprv prejdeme \(O(D[i])\) menších hodnôt \(P[j],D[j]\) a potom ešte potrebujeme porovnať dve \(D[i]\)-ciferné čísla, aby sme zistili, či môžu byť posledné dva úseky rovnako dlhé. A už vieme, že \(D[i] \leq \sqrt{2n}+1\).

Ak chceme program ďalej zrýchliť, potrebujeme vedieť rýchlo porovnávať dlhé čísla a tiež potrebujeme prechádzať menej hodnôt pri počítaní jednej dvojice \(P[i], D[i]\). Už sme si dokázali, že nemá zmysel, aby sa dĺžky susedných čísel líšili o viac ako dva. Takže nemusíme skúšať všetky možnosti, stačí pozrieť len hodnoty \(j \in \{D[i]-2, D[i]-1, D[i]\}\). Bohužiaľ, keď nepoznáme \(D[i]\), tak nevieme, ktoré možnosti skúšať.

Preto budeme tieto hodnoty počítať trocha inak – odpredu. Pekne od začiatku začneme počítať \(P\) a \(D\) pre hodnoty \(1,2,3,4,\dots\) A vždy, keď spočítame nejakú hodnotu, \(P[i]\) a \(D[i]\), vieme, ktoré vyššie hodnoty ovplyvnia. Aktualizujeme teda, hodnoty o \(D[i]\), \(D[i]+1\) a \(D[i]+2\) vyššie, čo už môžeme spraviť, lebo už poznáme \(D[i]\). Teda napríklad vieme, že \(P[i+D[i]+1]\) ani \(P[i+D[i]+2]\) nebude menej ako \(P[i]+1\). A zároveň vieme, že ak číslo pozostávajúce z cifier \(i-D[i]\) až \(i\) (polouzavretý interval) je menšie ako číslo pozostávajúce z cifier \(i\) až \(i+D[i]\), tak aj \(P[i+D[i]] > P[i]+1\).

Tieto myšlienky vieme zapísať do nasledujúceho programu, ktorý už je pomerne rýchly a získa 7 z 8 bodov.

#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
using namespace std;
#define For(i, n) for(int i = 0; i<int(n); ++i)

string dazdovka; // vstup

// porovnaj cisla, ktore maju 'dlzka' cifier a zacinaju na poziciach i1, i2
bool mensie(int i1, int i2, int dlzka) {
    For(i, dlzka) 
        if (dazdovka[i1+i] != dazdovka[i2+i])
            return dazdovka[i1+i] < dazdovka[i2+i];
    return false;
}

int main() {
    cin >> dazdovka;
    // pristupujeme do poli aj za n-tu poziciu, ale nikdy nie dalej ako rezerva
    int rezerva = dazdovka.size() + dazdovka.size()/10 + 100;
    vector<int> P (rezerva); // pocet kusov do pozicie i
    vector<int> D (rezerva); // dlzka kusa konciaceho na pozicii i
    P[0] = 0;
    D[0] = 1;

    For(i, dazdovka.size()+1) {
        if (!mensie(i, i-D[i], D[i])) {
            D[i+D[i]] = D[i];
            P[i+D[i]] = P[i]+1;
        }
        // vieme, ze predosle hodnoty neboli mensie, 
        // lebo sme ich mohli najst len s mensim i 
        D[i+D[i]+1] = D[i]+1;
        D[i+D[i]+2] = D[i]+2;
        P[i+D[i]+1] = P[i]+1;
        P[i+D[i]+2] = P[i]+1;
    }
    cout << P[dazdovka.size()] << endl;
}

Vzorové riešenie

Jediná vec, ktorá teraz spomaľuje beh programu je porovnávanie reťazcov. V najhoršom prípade porovnáme všetkých \(O(D[i])\) znakov, čo trvá \(O(\sqrt{n})\) času. Ale my predsa vieme porovnávať aj rýchlejšie, ak si dážďovku trocha predspracujeme.

Možností, ako zrýchliť porovnávanie je mnoho. Jeden z tých jednoduchších spôsobov je spraviť väčšie bloky cifier, ktoré budeme schopní porovnávať naraz.

Zvolíme si veľkosť bloku \(k\), následne zoberieme všetky možné kusy dážďovky dĺžky \(k\). Tieto kusy si radix-sortom utriedime a spočítame indexy – pre každú \(k\)-ticu si zapamätáme, koľká najmenšia \(k\)-tica zo všetkých to je.

Potom, keď budme chcieť porovnať dve dlhé čísla, tak môžeme najprv porovnať prvú \(k\)-ticu cifier, potom druhú \(k\)-ticu cifier a tak ďalej. Každú \(k\)-ticu porovnáme jedným pozretím do poľa indexov. Možno nám ešte na konci ostane niekoľko (najviac \(k\)) cifier, ktoré budeme musieť porovnať po jednej.

Časová zložitosť predpočítania indexov je \(O(nk)\) a časová zložitosť jedného porovnania reťazcov dĺžky \(\sqrt{n}\) je \(O(k + \sqrt{n}/k)\), čo je najmenej pre \(k = \sqrt[4]{n}\).

Takže dostaneme algoritmus s časovou zložitosťou \(O(n\sqrt[4]{n}) = O(n^{1.25})\). Pri implementácii si treba dávať pozor, že keď porovnávame dve \(k\)-tice, potrebujeme rozlišovať nielen dve možnosti menší/nie menší, ale tri možnosti väčší/menší/rovnaký.

V praxi je radix-sort pomerne pomalý, má zlú konštantu, takže v zdrojovom kóde sme nastavili konštantu \(k\) na \(10\) pre lepší čas (teoreticky by bolo lepšie \(k=30\), pretože to je približne \(\sqrt[4]{10^6}\)). Takto vyzerá funkcia predpocitaj, ktorú zavoláme raz hneď po načítaní vstupu a funkcia mensie, ktorá nahradí pôvodnú funkciu mensie.

// skok by mal byt priblizne stvrta odmocnina z n
#define skok 10
vector<int> poradie;

void predpocitaj(int n) {
    vector<int> D(n+skok+47,0);
    For(i,n) D[i] = dazdovka[i]-'0';

    vector<int> kusy (n);
    vector<int> vrecka[10];
    For(i, n) kusy[i] = i;

    For(i, skok) {
        For(j, n) vrecka[D[kusy[j]+skok-i-1]].push_back(kusy[j]);
        int p = 0;
        For(j, 10) {
            for(const auto &x : vrecka[j]) kusy[p++] = x;
            vrecka[j].clear();
        }
    }
    poradie.resize(n);
    For(i, n) {
        bool rovnake = (i > 0);
        if (rovnake) For(j, skok) 
            if (D[kusy[i-1]+j] != D[kusy[i]+j]) {
                rovnake = false;
                break;
            }
        if (rovnake) poradie[kusy[i]] = poradie[kusy[i-1]];
        else poradie[kusy[i]] = i+1;
    }
    poradie.resize(n+n/100+47, 0);
}

bool mensie(int i1, int i2, int dlzka) {
    int i = 0;
    for(; i < dlzka-skok; i+=skok) {
        if (poradie[i1+i] != poradie[i2+i])
            return poradie[i1+i] < poradie[i2+i];
    }
    for(; i < dlzka; ++i) {
        if (dazdovka[i1+i] != dazdovka[i2+i])
            return dazdovka[i1+i] < dazdovka[i2+i];
    }
    return false;
}

Táto myšlienka sa dala posunúť ešte ďalej a namiesto jednej sady blokov dĺžky \(k\) sme mohli mať bloky dĺžok \(1, 2, 4, 8, 16, 32, \dots, 2^{\log{n}}\). Predpočítať poradie blokov všetkých dĺžok vieme spraviť v čase \(O(n \log n)\), pretože vieme zistiť poradie blokov dĺžky \(2k\) v \(O(n)\), ak poznáme poradie blokov dĺžky \(k\).

Porovnávanie čísel, resp. funkcia mensie by potom bežala tiež v čase \(O(\log n)\), čím by sme dosiahli výbornú celkovú zložitosť \(O(n\log n)\).

Takéto riešenie stačilo na plný počet bodov aj za popis aj za program. Predošlé riešenie \(O(n^{1.25})\) by dostalo za program tiež plný počet a za dobrý popis by dostalo 11 bodov z 12.

Iný spôsob, ako dosiahnuť rýchle riešenie je hashovanie. Môžeme jednoduchým cyklom spočítať hash pre každý blok dlhý \(k\) cifier a potom zasa vieme porovnávať v čase \(O(k + \sqrt{n}/k)\).

Dobrá hash je napríklad \(\sum\limits_{i=1}^{k} {c_i 47^i} \mod p\), kde \(c_i\) je \(i\)-ta cifra čísla a \(p\) je nejaké veľké prvočíslo, napr. \(10^9 + 9\).

Spočítanie hash-hodnôt vieme spraviť v \(O(n)\) a tak je to v praxi oveľa rýchlejšie ako radix-sort. Nevýhoda je, že pri použití hashe nemáme istotu, že program odpovie správne, pretože dve rôzne \(k\)-ciferné čísla môžu mať rovnakú hash. Taktiež hash čísla nevie povedať, ktorá \(k\)-tica je menšia, vie len overovať rovnakosť. To nám však príliš nevadí.

Celková zložitosť tohto algoritmu by bola tiež \(O(n^{1.25})\).

Pomocou hash-funkcií vieme spraviť aj jednoduché riešenie so zložitosťou \(O(n \log n)\). Najprv si spočítame hash pre každý prefix dážďovky \(H_i = \sum\limits_{i=1}^{k} {c_i 47^i} \mod p\), kde \(c_i\) je \(i\)-ta cifra dážďovky.

Potom, ak chceme zistiť, či sú nejaké dva intervaly dážďovky \((a,b)\) a \((c,d)\) rovnaké, stačí zistiť, či \(((H_b - H_a)\cdot 47^c - (H_d - H_c)\cdot 47^a) \mod p == 0\).

Potom, ak ideme porovnávať dve dlhé čísla, vieme binárne vyhľadať prvú cifru v ktorej sa líšia a porovnať len tú. Takto dosiahneme zložitosť predpočítania \(O(n)\) a zložitosť jedného porovnania \(O(\log n)\).

typedef long long ll;
vector<ll> H; // hash prefixov dazdovky
vector<ll> powp; // mocniny cisla 47
ll prime = 47;
ll mod = 1000000009;

void predpocitaj(int n, int rezerva) {
    H.resize(rezerva+1);
    powp.resize(rezerva+1);
    powp[0] = 1;
    For(i, rezerva) powp[i+1] = (powp[i]*prime) % mod;
    H[0] = 0;
    For(i, rezerva) {
        int c = (i>n)?0:(dazdovka[i]-'0');
        H[i+1] = (H[i] + (powp[i]*c)) % mod;
    }
}

bool mensie(int i1, int i2, int dlzka) {
    // binarne vyhladame prvu cifru, kde sa lisia
    int b = 0, e = dlzka, m;
    while(e-b > 1) {
        m = (b+e)/2;
        ll h1 = ((H[i1+m] - H[i1]) * powp[i2]) % mod;
        ll h2 = ((H[i2+m] - H[i2]) * powp[i1]) % mod;
        if ((h1-h2)%mod == 0) b = m;
        else e = m;
    }
    return dazdovka[i1+b] < dazdovka[i2+b];
}

Bonusové riešenie

Všetkých vás určite zaujíma, či sa úloha nedala vyriešiť aj v čase \(O(n)\). Áno dala, ale zložitosť riešenia výrazne presahuje kategóriu O.

Bolo potrebné dotiahnuť do konca zrýchlenie porovnávania. Povieme si aspoň hlavnú myšlienku pre skúsených čitateľov. Nezúfajte, ak teraz neporozumiete skratkám a názvom algoritmov, keď budete starší, môžete sa k tomuto vzoráku vrátiť a skúsiť to znova.

Zostrojíme si pre dážďovku Suffixové pole. Potom, keď budeme chcieť porovnať dva rovnako dlhé kusy dážďovky, najprv overíme, či náhodou nie sú úplne rovnaké. Ak nie sú, tak vieme, že ich poradie je rovnaké ako poradie k nim prislúchajúcich suffixov. Takže ich porovnáme pomocou Suffixového poľa v \(O(1)\).

Ako však v \(O(1)\) zistiť, či sú kusy dážďovky rovnaké? Jednou možnosťou by bolo opäť hashovať, ale to nechceme, lebo hash nezaručuje správnosť riešenia. Namiesto toho si na začiatku spočítame LCP pole ku Suffixovému poľu a overíme, či minimum zo všetkých LCP medzi suffixami prislúchajúcimi porovnávaným kusom dážďovky je väčší alebo rovný ako dĺžka porovnávaných kusov. Ak áno, tak sú rovnaké, inak sú odlišné.

Takže potrebujeme rýchlo počítať minimum z nejakých intervalov v nejakom poli. Inak povedané, potrebujeme riešiť známy problém Range-Minimum-Query v čase \(O(n)\) na predspracovanie a \(O(1)\) na query. Pekné riešenie RMQ spomínajú páni Fischer a Heun vo svojom čĺanku z roku 2006. Vraveli sme, že to presahuje kategóriu O.

Ničmenej, dá sa to celé nakódiť, ale v praxi pre \(n\leq 10^6\) je už len zostrojenie Suffixového poľa pomalšie ako pôvodné \(O(n\sqrt n)\) riešenie. Takže máme pekný teoretický výsledok, že sa to celé dá v \(O(n)\) ale ponechajme radšej tento výsledok v teoretickej rovine.