4. Zapeklitá situácia vzorové riešenie

5
3 3 4 3 2

2
4
3 2 1 5

Nad touto úlohou sa bolo treba zamyslieť, možno si nakresliť pár príkladov a odpozorovať niekoľko vlastností, ktoré nám pomôžu ju vyriešiť. No najprv z rozprávky vybaľme trocha terminológie. Banditi a ich mierenie nám predstavuje vrcholy a hrany orientovaného grafu, v ktorom z každého vrchola vychádza práve jedna hrana.

Úvodné pozorovania

Je jasné, že ak sa náš graf skladá z viacerých komponentov, tie sa navzájom neovplyvňujú, lebo medzi nimi nevedie hrana označujúca strieľanie. Môžeme preto úlohu riešiť iba pre jeden súvislý komponent. Aj keď vo výslednom riešení túto skutočnosť nemusíme priamo použiť, zjednoduší nám jeho vymýšľanie.

Ďalej si môžeme všimnúť, že v každom komponente bude aspoň jeden šťastný bandita, ktorý prežije. Niekto v komponente totiž strieľa ako posledný a na to, z pochopiteľných dôvodov, musí byť nažive. Samozrejme, týmto výstrelom nevie zabiť sám seba.

Po chvíli kreslenia môžeme odpozorovať, že každý komponent v sebe obsahuje aspoň jeden cyklus. Ak totiž začneme v ľubovoľnom vrchole, ktorý si označíme \(v_0\) a prechádzame sled vychádzajúcich hrán, tak postupne navštevujeme vrcholy \(v_1, v_2, \dots\) Keďže z každého vrchola vychádza práve jedna hrana, a vrcholov máme len konečne veľa, týmto spôsobom navštívime vrchol, v ktorom sme už boli (teda pre nejaké \(j > i: v_j = v_i\)), a teda nájdeme cyklus.

Riešenie pre jeden komponent

Najskôr sa vrhnime na najjednoduchší prípad - jednoduchá kružnica. Na nej platí, že na každého banditu mieri práve jeden iný bandita.

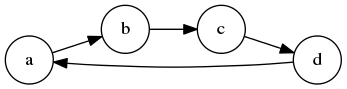
Pozrime sa, ako by vyzerala optimálna streľba. Keďže všetky vrcholy na kružnici sú rovnocenné a niekto musí začať strieľať, tak nech začne bandita \(c\) výstrelom na \(d\). Teraz ale bandita \(b\), ktorý naňho mieril, nemá stlačením spúšte čo pokaziť a tak vystrelí. Teraz však môže bez problémov vystreliť bandita \(a\). Ten už si môže vydýchnuť, lebo naňho mieriaci \(d\) už bol zastrelený, \(a\) teda prežije. Lepšie takýto graf už nevieme vyriešiť, lebo aspoň jeden bandita nám musí zostať nažive. Ľahko vidieť, že tento postup môžeme použiť aj na väčšie kružnice, ako aj najmenší možný prípad (dvaja na seba mieriaci banditi).

V samotnom programe takéto riešenie vieme vyrobiť tak, že si najskôr nájdeme jedného banditu na takejto kružnici (v našom príklade by to bol \(a\)). Z neho obehneme kružnicu po hranách, pričom si budeme vrcholy ukladať do pomocného vektora, a zastavíme keď narazíme na pôvodný vrchol. V našom príklade by v ňom zostali hodnoty \([a, b, c, d]\). Keď sa na tento vektor pozrieme od konca, získame správnu postupnosť výstrelov. Treba si však dať pozor na posledného banditu (\(d\)), ktorý nevystrelí, ale je zastrelený ako prvý. Jeho teda vypisovať nechceme.

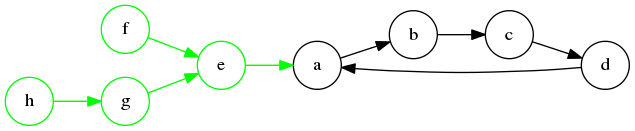
Nuž a čo ak komponent nie je len obyčajná kružnica? V takom prípade komponent vyzerá ako cyklus, do ktorého vedie niekoľko stromov (na obrázku je takýto strom vyznačený zelenou). V obyčajnom cykle nám musel zostať jeden bandita nažive, lebo strieľal ako posledný a už ho nemal kto ďalší zastreliť. Teraz však môžeme využiť to, že do kružnice mieri niekto iný.

Pozrime sa znova na náš obrázok a vezmime si riešenie predchádzajúcej časti. Vtedy sa nám postrieľali banditi \(b\), \(c\), \(d\) a nažive nám zostal \(a\). Tentokrát však máme banditu \(e\), ktorý ho môže zastreliť, a jeho zas môže zastreliť bandita \(f\) atď. Na kružnici teda neprežije nikto. Kto ale prežije na strome?

Vrcholy stromu, ktoré majú len jednu hranu nazývame listami. Je zjavné, že každý bandita, ktorý je v liste, prežije – nikto naňho totiž nemieri. Ďalej si ukážeme, že vieme nájsť postupnosť výstrelov, v ktorej zastrelíme každého iného banditu v strome.

Označme si vrchol, ktorým sa strom napája na kružnicu (\(e\)) ako koreň stromu. Pre každý list v strome vedie práve jedna cesta z listu do koreňa. Ak si vyberieme ľubovoľnú takúto cestu a postrieľame na nej postupne všetkých banditov (samozrejme, okrem listu), rozpadne sa nám strom na niekoľko menších stromov a stále bude platiť, že banditi, na ktorých nikto nemieri sú len pôvodné listy. Zmenšili sme strom na niekoľko menších a opakovaním tohto postupu nám zostanú len stromy s jedným vrcholom – pôvodné listy – preživší.

Naprogramovať sa to dá pomerne jednoducho. Vyberieme si náhodný list (\(f\)) a postrieľame banditov na ceste ku koreňu. Rovnako ako na kružnici si môžeme uložiť postupnosť vrcholov na ceste do poľa a pole potom obrátiť a pridať ku výslednej postupnosti. Strom sa nám rozpadne na dva menšie stromy – \(f, h \rightarrow g\).

Ak by sme teraz chceli postrieľať banditov v podstrome, tiež by sme vystrieľali cestu od niektorého listu ku koreňu (teda napríklad na ceste \(h, g\)). Môžeme si ale uvedomiť, že táto cesta leží na ceste od listu ku koreňu aj v pôvodnom strome (teda, \(h, g\) je súčasťou \(h, g, e\)). V implementácii si teda vôbec nemusíme pamätať menšie stromy, stačí pospúšťať cesty (streľby) z každého listu do koreňa a vždy zastreliť len tých banditov, ktorí ešte žijú.

Dokonca nemusíme vedieť ani ktoré vrcholy sú koreňmi. Jednoducho spustíme streľbu z listu a keď sa strom napojí na kružnicu, vystrieľa ju celú. Ďalšie postupnosti výstrelov už kružnicu nenavštívia, lebo strieľame len dovtedy, kým na ceste nenarazíme na mŕtveho banditu.

Výsledné riešenie

Naše riešenie teda vyzerá tak, že prejdeme cez všetky listy a postrieľame cestu, ktorá z nich vychádza, a následne prejdeme cez všetky kružnice.

Už potrebujeme len zistiť, ktoré vrcholy sú listy a ktoré sú na kružnici. O listoch vieme, že nebudú mať žiadne vstupné hrany, takže takže nám stačí spočítať si vstupné hrany každého vrcholu pri načítaní vstupu. O vrcholoch na kružnici zase vieme, že majú práve jednu vstupnú hranu. Tu už ale neplatí, že každý vrchol s jednou vstupnou hranou leží na kružnici (napríklad vrchol \(g\)). Avšak každý z takýchto vrcholov zastrelíme pri strieľaní od listov. Stačí nám teda najskôr prejsť vrcholy a strieľať od listov, a potom ich prejsť ešte raz a strieľať len živé vrcholy s jednou vstupnou hranou.

Pamäťová zložitosť bude \(O(n)\). Pre každého banditu si pamätáme len jeho cieľ, počet naňho mieriacich banditov a či je ešte nažive.

Časová zložitosť je tiež \(O(n)\). Pri strieľaní listov sa na každý vrchol pozrieme najviac dvakrát. Raz, keď sa pozrieme či to nie je list a raz, keď ho zastrelíme. Obdobne pri strieľaní kružnice.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<bool> nazive;
vector<int> ciel;
vector<int> vstupne;
vector<int> result;

void strielaj(int a) {
  if(!nazive[a]) return;

  vector<int> temp;   // na ukladanie vystrelov
  temp.push_back(a);  // ukladame od posledneho vystrelu po prvy
  int i = ciel[a];
  
  // zapiseme si zastrelenie dalsieho banditu a pokracujeme
  while(i != a && nazive[i]) {
    nazive[i] = false;
    temp.push_back(i);
    i = ciel[i];
  }

  // posledny striela na mrtveho alebo povodneho, to nechceme
  temp.pop_back();

  // vystrely mame ulozene od posledneho, ale chceme ich od prveho
  reverse(temp.begin(), temp.end());
  result.insert(result.end(), temp.begin(), temp.end());
}

int main(){
  int n;
  cin >> n;
  
  ciel.resize(n);
  nazive.resize(n, true);
  vstupne.resize(n, 0);

  // nacitame vstup, precislujeme vrcholy od 0, spocitame vstupne hrany
  for(int i=0; i<n; i++) {
    cin >> ciel[i];
    ciel[i]--;
    vstupne[ciel[i]]++;
  }

  // zastrelime od volnych koncov
  for(int i=0; i<n; i++)
    if (vstupne[i] == 0) strielaj(i);

  // zastrelime kruznice
  for(int i=0; i<n; i++) 
    if (vstupne[i] == 1) strielaj(i);

  int count = 0;
  for(int i=0; i<n; i++)
    if (nazive[i]) count++;

  cout << count << endl;

  cout << result.size() << endl;
  for(int i=0; i<result.size(); i++)
    if (i != result.size()-1)
      cout << result[i]+1 << " ";    // kedze sme precislovali po nacitani, tak precislujeme spat
    else
      cout << result[i]+1 << endl;    

  return 0;
}