Maximálne párenie v bipartitnom grafe

Párenie (angl. matching) je taká množina hrán grafu, pri ktorej ku každému vrcholu vedie najviac jedna hrana z tejto množiny. A keďže prázdna množina tvorí párenie, väčšinou nás zaujíma najväčšie možné párenie, ktoré vieme v grafe nájsť. Tento problém je pomerne ťažký, napriek tomu existuje polynomiálny algoritmus, ktorý ho rieši na ľubovoľnom grafe. (https://en.wikipedia.org/wiki/Blossom_algorithm) Oveľa častejšie sa však stretneme s párením na bipartitnom grafe, pri ktorého hľadaní vieme použiť jednoduchý algoritmus založený na prehľadávaní do hĺbky.

Formality

Zadefinujme si našu úlohu formálnejšie: Máme graf $G$. Párenie $M$ je podmnožina hrán grafu taká, že každý vrchol grafu $G$ je koncom najviac jednej hrany tejto podmnožiny. Inými slovami, každý vrchol je spárený s najviac jedným iným vrcholom. Samozrejme, naším cieľom je nájsť maximálne párenie.

Párenie sa štandardne hľadá postupným zväčšovaním už nájdeného párenia. Používajú sa na to takzvané zlepšujúce cesty.

$M$-alternujúca cesta je cesta v grafe $G$ taká, že všetky vrcholy v nej sú rôzne, a z každej dvojice po sebe nasledujúcich hrán je jedna v $M$ a druhá nie. Je to teda cesta, kde je každá druhá hrana v $M$.

$M$-zlepšujúca cesta je $M$-alternujúca cesta v grafe $G$ taká, že má nepárnu dĺžku a začína a končí v rôznych vrcholoch, z ktorých ani jeden nie je spárený v $M$.

Trik zlepšujúcej cesty spočíva v tom, že ak všetky hrany pozdĺž cesty, ktoré boli v $M$, z $M$ odstránime a všetky, ktoré neboli v $M$, do $M$ pridáme, tak dostaneme párenie, ktoré má o hranu viac. Preto platí, že kým vieme nájsť $M$-zlepšujúcu cestu, tak $M$ nie je maximálne.

Formálne si to vieme zadefinovať takto:

Ak $A$ a $B$ sú množiny, tak nech $A\Delta B$ je množina taká, že obsahuje prvky, ktoré sú v $A$ alebo v $B$, ale nie v oboch zároveň (je to akoby XOR množín $A$ a $B$).

Majme teda nejakú $M$-zlepšujúcu cestu $C$, kde $C$ je množina hrán z grafu $G$, ktoré ležia na tejto ceste. Potom $M' = M \Delta C$ je množina hrán, o ktorej vieme dokázať, že je párením, tak, že sa pozrieme na každý jeden vrchol a dokážeme, že je spárený s najviac jedným iným vrcholom. Ak vrchol $v$ neleží na ceste $C$, tak to znamená, že sa žiadna nová hrana k nemu pripojená nepridala do $M'$, a preto je stále spárený s najviac jedným iným vrcholom. Vrcholom na konci cesty $C$ sa pridala jedna nová hrana do $M$, ale doteraz neboli spárené, takže to nevadí. Ostatným vrcholom po ceste $C$ sa počet k nim pripojených hrán nezmenil, pretože každému sa zmenilo iba to, ktorá z jeho hrán je v $M$. Všetky tieto vrcholy už boli spárené predtým a sú spárené aj teraz. Všimnime si, že na ceste $C$ bolo menej hrán v $M$ ako mimo $M$ - pretože hrany sa striedali, ale prvá a posledná neboli v $M$. To ale znamená, že v $M' $ bude na ceste $C$ viac hrán ako mimo $M'$. Tým pádom v $M'$ je viac hrán a teda je to väčšie párenie.

Z tohto vyplýva, že ak nájdeme $M$-zlepšujúcu cestu, tak ju vieme skoro zadarmo zlepšiť z $M$ na $M'$.

Ak v bipartitnom grafe nie je $M$-zlepšujúca cesta

V bipartitných grafoch to však platí aj opačne. Keď neexistuje $M$-zlepšujúca cesta, tak $M$ je maximálne párenie.

Toto si vieme opäť veľmi pekne dokázať: Nech $M$ je ľubovoľné párenie. Ak existuje párenie väčšie od $M$, tak existuje aj také párenie $M'$, ktoré je od $M$ väčšie presne o jednu hranu. Pozrime sa na $X:= M \Delta M'$. Množinu $X$ vieme dostať tak, že spojíme prvky, ktoré sú v $M$ a $M'$, a dvakrát odstránime prvky, ktoré boli v oboch pôvodných množinách. Lenže keď $M'$ je väčšia množina ako $M$, tak aj v $X$ je viac hrán z $M'$ ako z $M$. Preto keď sa pozrieme na komponenty $X$, tak v nejakom z nich musí byť viac hrán z $M'$ ako z $M$.

Každý vrchol je pripojený k najviac jednej hrane v $M$ aj v $M'$. Preto každý vrchol je pripojený k najviac dvom hranám v $X$. Tým pádom $X$ sa môže skladať iba z dvoch druhov komponentov: ciest a kružníc. Zoberme si ľubovolný komponent v $X$, v ktorom je viac hrán z $M'$ ako z $M$. Nemôže to byť cyklus, pretože na cykle sa rovnomerne striedajú hrany z $M'$ a $M$, a preto ich je rovnako veľa. Ak je to cesta, tak aj na nej sa striedajú hrany z $M$ a $M'$, ale tam môže byť o jednu hranu z $M'$ viac, keďže sa cesta môže začínať aj končiť hranou z $M'$. Táto cesta je však $M$-zlepšujúca, pretože sa na nej striedajú hrany v $M$ a mimo $M$ a koncové vrcholy v $M$ nie sú spárené (inak by to nebol koniec cesty v $X$).

Dokázali sme, že vždy, keď existuje párenie s väčším počtom hrán, ako má ľubovolné párenie $M$, tak $M$ môžeme zlepšiť nájdeným $M$-zlepšujúcej cesty, ktorá určite existuje.

Ako hľadať zlepšujúce cesty

DFS/BFS

Každá $M$-zlepšujúca cesta v bipartitnom grafe má jeden koniec v $A$ (ľavej časti grafu) a druhý koniec v $B$ (pravej časti grafu). Z každého nespáreného vrcholu v $A$ teda môžeme ísť hľadať cestu do nespáreného vrcholu v $B$. Vždy, keď sa dostaneme do vrcholu v $B$, tak buď je nespárený a našli sme k nemu $M$-zlepšujúcu cestu z nespáreného vrcholu v $A$, alebo je spárený a vtedy môžeme využiť jeho hranu ku s ním spárenému vrcholu v $A$ a pokračovať v hľadaní zlepšujúcej cesty odtiaľ. Vždy, keď nájdeme zlepšujúcu cestu, párenie aktualizujeme a môžeme celé hľadanie zopakovať.

Keď je veľkosť maximálneho párenia $|M|$, tak časová zložitosť tohto postupu je $O(|M|E)$, kde $E$ je počet hrán v grafe.

// Inspirovane KACTL
#include <iostream>
#include <vector>
using namespace std;
bool DFS(int b, vector<vector<int>>& G, vector<int>& z_b_do_a, vector<int>& navstivene) {
    //ak tento vrchol nie je spareny, tak sme prave nasli vrchol, v ktorom sa moze skoncit zlepsujuca cesta
    if (z_b_do_a[b] == -1) return 1;

    //inak tento vrchol musi uz byt spareny s vrcholom a v A
    int a = z_b_do_a[b];

    //oznacime si tento vrchol ako navstiveny
    navstivene[b] = 1;

    for (int e : G[a])
        // ak ma A suseda, ktoreho sme este nenavstivili, skusime ho navstivit a zistit, ci z neho nevedie cesta parnej dlzky do nespareneho vrcholu
        if (!navstivene[e] && DFS(e, G, z_b_do_a, navstivene)) {
            // ak vedie, tak pri vynarani sa z nej chceme updatovat parenie
            // chceme, aby e bolo teraz sparene s vrcholom, s ktorym predtym nebolo - a
            z_b_do_a[e] = a;
            return 1;
        }
    return 0;
}
int najvacsie_parenie(vector<vector<int>>& G, vector<int>& z_b_do_a) {
    vector<int> vis;
    int ans = 0;
    //skusame ziskat parenie pre kazdy vrchol v A, ak raz nejaky sparime, tak uz zostane spareny
    for(int a=0; a < G.size(); a++) {

        //budeme si ukladat, ktore vrcholy v B sme uz videli
        vis.assign(z_b_do_a.size(), 0);

        // pre tento vrchol v A sa pozrieme na vsetkych jeho susedov a z kazdeho z nich sa snazime najst alternujucu cestu k nesparenemu vrcholu v B, moze byt aj dlzky 0
        // ak je dlzky 0, tak aj to je vhodny kandidat na sparenie
        for (int b : G[a])
            if (DFS(b, G, z_b_do_a, vis)) {
                //ak toto DFS bolo uspesne, nesmieme zabudnut zmenit vrchol spareny s b na a a zvysit celkovy pocet hran v pareni o 1
                z_b_do_a[b] = a;
                ans++;
                break;
            }
    }
    return ans;
}
int main() {
    int A, B, m;
    cin >> A >> B >> m; //pocet vrcholov nalavo, pocet vrcholov napravo a pocet hran
    vector<vector<int>> G(A);
    for(int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b; //vrcholy nalavo cislujeme od 0 po A-1, napravo od 0 po B-1
        G[a].push_back(b);
    }
    vector<int> z_b_do_a(B, -1);
    cout << najvacsie_parenie(G, z_b_do_a) << endl;
    // vypiseme, ktore vrcholy v A su sparene s ktorymi vrcholmi v B.
    for(int i = 0; i<B; i++) {
        if(z_b_do_a[i]!=-1)
            cout << z_b_do_a[i] <<" "<< i << endl;
    }
}

Hopcroft - Karp

Existuje aj rýchlejší algoritmus, ktorý beží v časovej zložitosti $O(\sqrt{V}E)$, kde $V$ je počet vrcholov v grafe.

Tento algoritmus robí v každej iterácii BFS na to, aby našiel najkratšiu cestu ku každému vrcholu po zlepšujúcich cestách. Keď BFS nájde najkratšiu cestu do vrcholu v $B$, tak pozdĺž týchto ciest robí DFS prechádzajúc naspäť od konca smerom na začiatok, kde tieto cesty upravuje v zozname najkratších ciest. Vždy, keď nejakú cestu použije, tak všetky vrcholy na nej pre túto iteráciu označí ako použité a pokúsi sa nájsť ďaľšiu cestu. Aj keď je tento krok spravený nehospodárne, greedy/pažravým spôsobom (jedna zlepšujúca cesta môže zabrániť použitiu inej a my nijako neošetrujeme, aby sa to nestávalo), tak sa dá dokázať, že v každej iterácii BFS bude najkratšia zlepšujúca cesta dlhšia ako v predošlej iterácii. Tým pádom po $\sqrt{V}$ iteráciach bude mať najkratšia zlepšujúca cesta dĺžku aspoň $\sqrt{V} $. Nech párenie po $\sqrt{V}$ iteráciách je $M$. Nech $M'$ je optimálne párenie. Potom zadefinujme $X:= M \Delta M'$. Ako sme už dokázali vyššie, komponenty tohto grafu obsahujú cykly a cesty. Všetky zlepšujúce cesty v tomto grafe majú dĺžku aspoň $\sqrt{V}$ a preto je ich najviac $\sqrt{V}$. Všimnime si, že každá cesta predstavuje zvýšenie maximálneho párenia o 1 a v prípade, že ju použijeme, tak nám z tohto grafu akoby zmizne. Keď použijeme všetky z nich, tak dostaneme maximálne párenie. To znamená, že po $\sqrt{V}$ iteráciách nám chýba do maximálneho párenia najviac $\sqrt{V}$ vrcholov a teda najviac $\sqrt{V}$ ďaľších iterácii. Tým pádom má tento algoritmus najviac $O(\sqrt{V})$ zlepšujúcich iterácii a každá z nich trvá $O(E)$ času.

Viac o tomto algoritme môžete nájsť napríklad na Wikipédii.

Minimálne vrcholové pokrytie a Königova veta

Množina vrcholov $T$ sa nazýva vrcholové pokrytie, ak každá hrana v grafe $G$ má aspoň jeden koncový vrchol v $T$. Minimálne vrcholové pokrytie je také vrcholové pokrytie pre daný graf $G$, ktoré má najmenej vrcholov.

Königova veta hovorí, že v bipartitnom grafe minimálne vrcholové pokrytie má toľko vrcholov, koľko má maximálne párenie hrán.

Keďže žiadne dve hrany v maximálnom párení nemajú spoločný vrchol, tak musí každá z nich byť pokrytá iným vrcholom v minimálnom vrcholovom pokrytí. Preto má minimálne vrcholové pokrytie aspoň toľko vrcholov, koľko má maximálne párenie hrán. Teraz nám už stačí dokázať, že existuje vrcholové pokrytie, ktoré má presne toľko vrcholov, koľko má maximálne párenie hrán.

To dokážeme konštrukciou.

Definujme si:

• Množina $X_0$ = nespárené vrcholy v $A$.
• Množina $X$ = vrcholy v $A$, ktoré sú spojené s nejakým vrcholom v $X_0$ $M$-alternujúcou cestou
• Množina $Y$ = vrcholy v $B$, ktoré sú spojené s nejakým vrcholom v $X_0$ $M$-alternujúcou cestou

Všimnime si, že všetky vrcholy v $X_0$ sú aj v $X$, keďže $M$-alternujúca cesta môže mať aj nulovú dĺžku.

Tvrdenie 1: Všetky vrcholy v $Y$ sú spárené v $M$.

Dôkaz: Ak by vrchol $b \in Y$ nebol spáreaný v párení $M$, tak potom by k nemu existovala $M$-alternujúca cesta z nejakého vrcholu v $X_0$, čo je vlastne $M$-zlepšujúca cesta, a teda $M$ by nebolo maximálne párenie. To je však spor.

Tvrdenie 2: Neexistuje hrana medzi žiadnym vrcholom z $X$ a vrcholom z $B \backslash Y$ (množina vrcholov, ktoré sú v $B$, ale nie v $Y$).

Dôkaz: Nech taká hrana existuje medzi vrcholom $a\in X$ a $b\in B\backslash Y$. Potom existuje $M$-alternujúca cesta z $a_0 \in X_0$ do $a$, ktorá má párnu dĺžku a začína hranou, ktorá nie je v $M$, a preto končí hranou v $M$. Ak je hrana medzi $a$ a $b$ v párení $M$, tak potom tá cesta zjavne končí touto hranou (končí vo vrchole $a$ a vrchol $a$ je spárený jedine s touto hranou), a preto, keď ju skrátime o túto hranu, dostaneme $M$-alternujúcu cestu do $b$, a teda $b \in Y$, čo je spor. Ak hrana medzi $a$ a $b$ nie je v párení $M$, tak tú $M$-alternujúcu cestu vieme predĺžiť do $b$, a preto $b \in Y$, čo je zase spor.

Tvrdenie 3: V párení $M$ nie sú žiadne hrany medzi vrcholmi v $Y$ a vrcholmi v $A \backslash X$.

Dôkaz: Ak by bola v maximálnom párení $M$ taká hrana, ktorá je medzi vrcholom $b \in Y$ a vrcholom $a\in A$, tak potom by existovala $M$-alternujúca cesta do $b$, ktorá končí hranou v $M$, a teda by musela viesť cez $a$. To by ale znamenalo, že $a\in X$, čo je tiež spor.

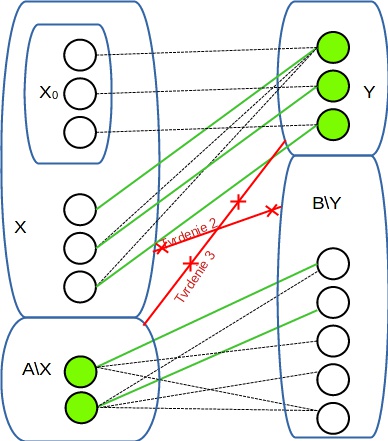
Nech $C$ je $Y \cup (A\backslash X)$. Podľa tvrdenia 2 je každá hrana pokrytá nejakým vrcholom v $C$, a preto je $C$ vrcholové pokrytie.

Podľa tvrdenia 1 je každý vrchol v $Y$ spárený. Podľa tvrdenia 3 každá hrana spárená v $M$ s vrcholom v $Y$ má na druhej strane práve jeden rôzny vrchol z $X \backslash X_0$. Preto $|Y| = |X \backslash X_0|$ . Každý vrchol v $A \backslash X$ je spárený v $M$, ale zjavne s vrcholom, ktorý je v $B$, ale nie v $Y$ (podľa tvrdenia 3).

Párenie $M$ má veľkosť $|M| = |A \backslash X_0| = |A\backslash X| + |X \backslash X_0| = |A \backslash X| +|Y| = |C|$ .

Tým pádom sme našli vrcholové pokrytie s rovnakým počtom vrcholov, ako má najväčšie párenie hrán.

Z programátorského hľadiska, keď máme maximálne párenie, tak ľahko nájdeme vrcholy v $X_0$, z ktorých spustíme DFS/BFS na hľadanie vrcholov v $X$ a $Y$. Z toho zistíme $C$, čím skonštruujeme minimálne vrcholové pokrytie.

//najde vrcholove pokrytie, vyuziva minimalne parenie
vector<int> vrcholove_pokrytie(vector<vector<int>>& g, int A, int B) {
    vector<int> z_b_do_a(B, -1);
    int res = najvacsie_parenie(g, z_b_do_a);
    vector<bool> X(A, true), Y(B);

    //oznaci vrcholy, ktore su sparene, ako tie, ktore zatial nie su v X, vsetky ostatne su v X0
    for (int b : z_b_do_a) if (b != -1) X[b] = false;

    // kedze nam nezalezi na poradi vrcholov pocas vyhladavania (chceme iba najst vrcholy v X), tak mozeme namiesto fronty pouzit vector ako stack
    vector<int> q, C;
    // na zaciatku do stacku prehladavanych vrcholov pridame vrcholy z X_0
    for(int i=0; i<A; i++) if (X[i]) q.push_back(i);


    while (!q.empty()) {
        int a = q.back(); q.pop_back();
        // pridame vrchol a do X
        X[a] = true;
        for (int b : g[a]) if (!Y[b] && z_b_do_a[b] != -1) {
            // ak sme vrchol b doteraz nevideli a je spareny, tak ho pridame do Y
            // ak je spareny, tak sa uz nechceme vracat po hrane, v ktorej sme uz boli
            Y[b] = true;
            q.push_back(z_b_do_a[b]);
        }
    }
    // na zaver precislujeme vrcholy napravo a vratime vector vrcholov v najmensom vrcholovom pokryti
    for(int i = 0; i < A; i++) if (!X[i]) C.push_back(i);
    for(int i = 0; i < B; i++) if (Y[i]) C.push_back(A + i);
    return C;
}

Najväčšia nezávislá množina

Pre daný graf $G$ množina vrcholov $S$ je nezávislá, keď medzi žiadnou dvojicou vrcholov v $S$ nie je hrana v grafe $G$.

Nájsť nezávislú množinu v grafe je jednoduché: Napríklad prázdna množina $S$ je nezávislá v každom grafe. Často však hľadáme najväčšiu nezávislú množinu. Táto úloha patrí na všeobecných grafoch k NP-úplným, čo znamená, že predpokladáme, že na ňu neexistuje riešenie v polynomiálnom čase, a ak by aj náhodou existovalo, našli by sme riešenie v polynomiálnom čase na stovky ďaľších úloh. Existuje na ňu však polynomiálne riešenie v prípade, že daný graf je bipartitný. Táto úloha je totiž úzko spojená s úlohou nájdenia minimálneho vrcholového pokrytia.

Ak $T$ je vrcholové pokrytie, tak $V\backslash T$ je nezávislá množina, pretože každá hrana v $G$ má aspoň jeden koniec v $T$, čo znamená, že v $V\backslash T$ nie je žiadna dvojica vrcholov taká, že by medzi nimi bola hrana v $G$.

Podobne, ak $S$ je nezávislá množina, tak $V \backslash S$ je vrcholové pokrytie, keďže každá hrana má najviac jeden vrchol v $S$ a teda aspoň jeden vrchol v $V\backslash S$.

Tým pádom ku každej nezávislej množine patrí práve jedno vrcholové pokrytie a súčet ich veľkostí je rovný počtu vrcholov. Z toho vyplýva, že k najväčšej nezávislej množine patrí najmenšie vrcholové pokrytie. To už nájsť vieme a najväčšia nezávislá množina je potom iba jeho doplnok.