Halda

V tomto texte si budeme rozprávať o haldách: jednoduchých stromových dátových štruktúrach, ktoré nám umožňujú udržiavať si údaje "tak trochu usporiadané". Ukážeme si, ako sa to robí a na čo je to dobré.

Počas vysvetľovania sa v tomto texte budú zjavovať obrázky rôznych stromov. Nebojte sa ich. Nebude ich treba implementovať. Keď sa úspešne dostaneme až na koniec našich úvah, ukáže sa, že nám bude stačiť jedno obyčajné pole.

Prioritná fronta

Naším hlavným cieľom v tomto článku bude efektívna implementácia takzvanej prioritnej fronty. Toto je dátová štruktúra, ktorá vie efektívne robiť dve operácie:

• push(prvok,priorita): vlož nový prvok a nastav mu konkrétnu prioritu
• pop(): vyber prvok, ktorý má spomedzi všetkých aktuálne uložených prvkov najväčšiu prioritu

Prioritnú frontu si teda vieme predstaviť ako čakáreň na pohotovosti. Postupne nám prichádzajú pacienti, každý s inou prioritou -- niekto je na tom lepšie, niekto horšie. No a vždy, keď sa ordinácia uvoľní, ošetrujúci lekár do nej zoberie pacienta s najväčšou prioritou, teda toho, kto najakútnejšie potrebuje ošetrenie.

Iné implementácie prioritnej fronty

Prioritnú frontu sa dá implementovať rôzne. Najjednoduchším spôsobom je samozrejme pamätať si aktuálnu množinu prvkov a ich priorít v obyčajnom poli. (Prípadne môžeme použiť pole premennej veľkosti, ako napr. vector v C++.) Pri takejto implementácii vieme operáciu push spraviť v konštantnom čase. Problém však nastáva pri operácii pop: aby sme našli prvok s najväčšou prioritou, potrebujeme prejsť a skontrolovať všetky prvky v poli. Táto operácia teda bude mať až lineárnu časovú zložitosť. Ak by sme teda mali postupnosť $n$ operácií push a $n$ operácií pop v nejakom neznámom poradí, môže jej spracovanie dokopy vyžadovať až $\Theta(n^2)$ krokov.

Podobne zlý je aj opačný extrém: udržiavať si poprvky v poli usporiadanom podľa priority (tak, aby prvok, ktorý chceme najskôr spracovať, bol na konci poľa). Tentokrát vieme operáciu pop robiť v konštantnom čase, no platíme za to tým, že pri každej operácii push musíme nájsť správne miesto, kam do poľa patrí nový prvok, a následne v lineárnom čase prvky poľa poposúvať, aby sme na nový prvok mali miesto.

Hľadáme teda nejaký "trade-off" -- nejaké riešenie, ktoré by bolo akoby na polceste medzi vyššie popísanými dvoma riešeniami. Jedným takýmto riešením je použiť na implementáciu prioritnej fronty vyvažovaný binárny strom, v ktorého vrcholoch si budeme jednotlivé prvky pamätať usporiadané podľa priority. Do takéhoto stromu obsahujúceho $n$ prvkov vieme v čase $O(\log n)$ aj vložiť nový prvok, aj nájsť a odstrániť z neho maximum.

Takéto riešenie je však zbytočne zložité na implementáciu. V tomto texte si ukážeme, ako tie isté časové zložitosti dosiahnuť omnoho jednoduchším programom.

Technický detail o prvkoch a prioritách

V nasledujúcom texte si pre jednoduchosť budeme zaoberať haldami, v ktorých sú uložené obyčajné prirodzené čísla. Pri skutočnom použití haldy tieto čísla predstavujú priority prvkov uložených v halde. Ak teda napríklad na nižšie uvedenom obrázku vidíte krúžok a v ňom číslo 47, toto číslo môže napríklad predstavovať celý záznam o pacientovi, ktorého priorita v čakárni je 47.

Podobne, keď budeme písať "prvok X je väčší ako prvok Y", myslíme tým, že X má väčšiu prioritu.

Všeobecná maximová halda

Maximová halda je zakorenený strom, v ktorom platí: prvok uložený v hociktorom vrchole je väčší alebo rovný ako každý z prvkov uložených v synoch daného vrcholu. Túto vlastnosť budeme volať podmienka haldy

(Analogicky existuje aj minimová halda, kde uvažujeme opačnú podmienku -- prvok uložený v hociktorom vrchole musí byť menší alebo rovný ako každý z prvkov uložených v jeho synoch.)

Všimnite si, že z podmienky haldy vyplýva, že pre ľubovoľný vrchol $v$ haldy platí, že hodnota v ňom je najväčšia z hodnôt v celom podstrome s koreňom $v$. (Totiž hodnota vo $v$ je väčšia alebo rovná ako hodnoty v jeho synoch, tie sú zase väčšie alebo rovné ako hodnoty v ich synoch, a tak ďalej.)

V koreni haldy je teda nutne vždy uložený najväčší zo všetkých prvkov v halde.

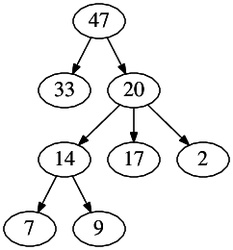
Cvičenie 1

Zamyslite sa teraz nad nasledujúcimi otázkami. Vo všetkých otázkach predpokladáme, že máme maximovú haldu a že prvky v nej sú navzájom rôzne.

• Kde všade sa môže nachádzať druhý najväčší prvok?
• Kde všade sa môže nachádzať tretí najväčší prvok?
• Kde všade sa môže nachádzať najmenší prvok?
• Kde všade sa môže nachádzať druhý najmenší prvok?

[Stručné riešenia cvičení nájdete na konci tohto textu.]

Vkladanie prvku do haldy

Predstavme si, že už odniekiaľ máme maximovú haldu: niekto už vybral konkrétny tvar stromu a rozmiestnil prvky do jeho vrcholov tak, aby spĺňali podmienku haldy. Ako vieme do takejto haldy pridať ďalší prvok?

Spravíme to veľmi jednoducho. Začneme tým, že nový prvok pridáme ako nový list kamkoľvek do stromu. Označme nový vrchol $v$ a jeho otca $u$. Vieme, že doteraz každý vrchol spĺňal podmienku haldy. Keď sme do stromu pridali vrchol $v$, jediné miesto, kde sme ju mohli pokaziť, je vrchol $u$, presnejšie hrana z $u$ do $v$.

Ak je táto hrana v poriadku (čiže ak je prvok vo vrchole $u$ väčší alebo rovný od nového prvku vo vrchole $v$), máme opäť haldu a sme hotoví. V opačnom prípade treba haldu upraviť.

Počas úpravy nebudeme vôbec meniť tvar našej haldy, len šikovne povymieňame prvky medzi sebou. Začneme v práve pridanom liste. Ako opraviť podmienku haldy pre hranu $uv$? Jednoducho: vymeníme prvky uložené v týchto dvoch vrcholoch.

V tomto okamihu už máme podmienku haldy určite splnenú vo vrchole $u$. Tento vrchol mohol mať pod sebou aj iných synov okrem $v$, no keďže pôvodná halda bola v poriadku a výmenou sme do vrcholu $u$ presunuli prvok väčší ako ten, čo tam bol doteraz, podmienku haldy sme tým nemali ako pokaziť.

Opäť teda existuje jediné miesto v celom strome, kde môže ešte byť pokazená podmienka haldy. Týmto miestom je hrana z vrcholu $u$ do jeho otca. A toto je presne tá istá situácia, v ktorej sme boli na začiatku (len sme v strome o úroveň vyššie). Opakujeme teda ten istý postup.

V najhoršom prípade tento postup skončí tým, že sa dostaneme až do koreňa celej haldy. Ten už nad sebou nič ďalšie nemá, takže v tej chvíli už je všade splnená podmienka haldy a môžeme skončiť.

Postup, ktorý sme si práve popísali, sa zvykne nazývať bublanie dohora, lebo sa naň dá dívať tak, že naposledy pridaný prvok postupne stúpa haldou až kým nepríde na miesto, kam patrí.

Vyberanie prvku s najväčšou prioritou

Vieme už, že najväčší prvok sa nachádza v koreni. Keď ho však chceme z haldy vybrať, potrebujeme nový koreň. Toto sa dá riešiť veľa spôsobmi, my si ukážeme jeden z nich. Budeme postupovať nasledovne:

1. Vyberieme prvok z koreňa a odložíme si ho nabok. Toto je prvok, ktorý chceme vrátiť ako výstup z našej funkcie, najskôr ale musíme po sebe upratať.
2. Strom má naďalej ten istý tvar ako mal doteraz, len v koreni je prázdne miesto.
3. Vyberieme si ľubovoľný jeden list, ktorý sa nám páči. Ten odstránime (čím zmeníme tvar stromu). Hodnotu, ktorá bola doteraz uložená v odstránenom liste, umiestnime na voľné miesto do koreňa.
4. Dostali sme teraz korektnú haldu? Zrejme nie. Ale ak nie, jediné miesto, kde môže byť porušená podmienka haldy, je samotný koreň. Toto opravíme (spôsobom, ktorý si popíšeme nižšie).

Na opravu haldy použijeme proces veľmi podobný tomu, ktorý sme používali pri vkladaní, len pôjdeme opačným smerom. Tomuto procesu sa teda bude hovoriť bublanie dodola.

Máme teda nejaký vrchol $v$, ktorý nespĺňa podmienku haldy. (Na začiatku je to koreň.) To znamená, že v aspoň jednom z jeho synov je väčší prvok ako vo $v$. Nech $u$ je ten syn, v ktorom je najväčší prvok zo všetkých synov vrcholu $v$. Vymeňme hodnoty v $u$ a $v$.

Čo sme tým dosiahli? Zjavne po tejto výmene už platí podmienka haldy pre vrchol $v$. (Nová hodnota vo $v$ je väčšia aj od tej, ktorá tam bola doteraz, a je väčšia alebo rovná od hodnôt v ostatných synoch vrcholu $v$.) Mohli sme ju však pokaziť vo vrchole $u$, do ktorého sme presunuli menšiu hodnotu. Spravíme teda to isté ako pri bublaní dohora -- znova zopakujeme ten istý postup, len s vrcholom $u$. Takto hodnotu z koreňa posúvame hlbšie a hlbšie dolu stromom, až kým sa nedostane na úroveň, kam patrí -- čiže buď do listu, alebo do nejakého vrcholu, pod ktorým už sú samé prvky s ešte menšou prioritou ako ten, ktorý práve buble dodola.

Cvičenie 2

Predstavme si, že vykonávame vyššie popísaný algoritmus: presunuli sme nejaký prvok z listu do koreňa a potom sme ho trikrát "prebublali" hlbšie. Teraz sa tento prvok nachádza vo vrchole $x$. Prezrieme všetkých synov vrcholu $x$ a nájdeme syna $y$, ktorý obsahuje najväčší prvok spomedzi nich. Ten je väčší aj od toho nášho, vymeníme ich teda medzi sebou. Ako sme spomenuli vyššie, touto výmenou sme mohli pokaziť podmienku haldy vo vrchole $y$, do ktorého sme presunuli menší prvok ako mal doteraz.

Všimnime si ale, že do vrcholu $x$ sme práve presunuli väčší prvok ako tam bol doteraz. Nemohli sme takto pokaziť podmienku haldy aj na hrane z vrcholu $x$ do jeho otca?

Zamyslenie nad časovou zložitosťou

Krok bublania dohora vieme implementovať v konštantnom čase: stačí porovnať dva prvky a ak treba tak ich vymeniť. Krok bublania dodola vieme implementovať v čase priamo úmernom stupňu spracúvaného vrchola, musíme totiž prezrieť všetkých jeho synov.

Dokopy teda platia nasledovné odhady časovej zložitosti:

• Vkladanie nového prvku má časovú zložitosť nanajvýš priamo úmernú hĺbke, do ktorej ho pridáme ako list.
• Výber maximálneho prvku má časovú zložitosť, ktorú vieme zhora odhadnúť ako (hĺbka našej haldy) krát (maximálny stupeň vrcholu v nej).

Ako teraz dosiahnuť, aby tieto časové zložitosti boli obe malé? A ako dosiahnuť, aby sa nám to celé ľahko implementovalo a aby sme sa nemuseli trápiť napríklad s pointrami?

Odpoveď na obe otázky je rovnaká: vhodne si zvolíme tvar našej haldy.

V doterajšom texte sme sa vôbec nezamýšľali nad tým, ako naša halda vyzerá -- či je plytká alebo hlboká, či sú stupne vrcholov malé alebo veľké. Tu však máme úplnú voľnosť: my si môžeme zvoliť taký tvar, ktorý bude mať aj dobré parametre, aj sa nám bude ľahko implementovať.

Zlé tvary haldy

Haldy rôznych degenerovaných tvarov nám príliš nepomôžu. Napr. je nanič halda, ktorá je tvorená jedným koreňom a $n-1$ listami. A takisto je nanič halda-had, v ktorej má každý vrchol najviac jedného syna.

V čom je problém?

Pozrime sa najskôr na prvú spomínanú haldu. Keby sme v našom programe používali haldu, ktorá vyzerá takto, príliš by nám to nepomohlo. Zjavne do takejto haldy vieme ľahko vkladať ďalšie prvky -- stačí pridať nový list a ak treba, tak hodnotu v ňom vymeniť s hodnotou v koreni. Avšak do problémov sa dostávame v okamihu, keď by sme chceli najmenší prvok z haldy vybrať. Vtedy by sme totiž na to, aby sme zistili, ktorú hodnotu presunúť do koreňa, museli prezrieť úplne všetky prvky v halde. Vieme teda robiť push v konštantnom čase, ale na pop potrebujeme až lineárny čas. (Takáto halda v podstate zodpovedá ukladaniu prvkov v neusporiadanom poli, až na to, že aktuálne maximum máme akoby v samostatnej premennej.)

A o nič lepšie na tom nie je ani druhá spomínaná halda. Vždy, keď vložíme nový prvok, ho pridáme ako nový list do najhlbšej úrovne a následne hodnotou z neho bubleme dohora, až kým sa nezastaví. V najhoršom možnom prípade (ktorý nastane, ak budeme vkladať prvky v poradí od najmenšieho po najväčší) teda každý prvok postupne prebuble hore celou reťazou až do koreňa. Teda druhý vložený prvok bude bublať dohora $1$-krát, tretí $2$-krát, \dots, a ak ich vložíme postupne $n$, tak posledný bude bublať dohora až $(n-1)$-krát. Tu teda operácia push môže trvať až lineárne dlho. A niet divu: ľahko nahliadneme, že takáto halda čítaná zhora dole je vlastne obyčajným usporiadaným poľom.

Jeden možný dobrý tvar haldy

Z odhadov časovej zložitosti je jasné, ako by mala dobrá halda vyzerať: mala by mať malú hĺbku a mala by zároveň mať malé stupne vrcholov. Existujú rôzne typy stromov, ktoré toto spĺňajú. Asi najjednoduchším typom sú takzvané takmer úplné binárne stromy.

Pripomeňme si, že v binárnom strome môže každý vrchol mať nanajvýš dvoch synov -- jedného ľavého a jedného pravého. A tiež si pripomeňme, že hĺbka vrcholu je definovaná ako počet hrán na ceste z neho do koreňa.

Binárny strom môžeme rozdeliť na úrovne. Úroveň $k$ tvoria všetky vrcholy, ktoré majú hĺbku $k$. Všimnime si, že na úrovni $k$ môžeme mať nanajvýš $2^k$ vrcholov. (Na úrovni 0 je len koreň, ten má nanajvýš 2 synov ktorí tvoria úroveň 1, každý z nich má nanajvýš 2 synov ktorí spolu tvoria úroveň 2, atď.)

Binárny strom voláme úplný, ak je každá jeho úroveň buď prázdna alebo úplne plná -- inými slovami, ak má každý vrchol v každej úrovni okrem poslednej práve dvoch synov. Úplný binárny strom hĺbky $k$ má teda presne $1+2^1+\cdots+2^{k-1}+2^k = 2^{k+1} - 1$ vrcholov, a z nich $2^k$ sú listy.

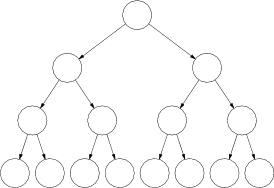
Zjavne pre skoro žiadne $n$ neexistuje úplný binárny strom s $n$ vrcholmi. Budeme sa teda musieť uspokojiť so stromami, ktoré sa na úplné dostatočne podobajú.

Takmer úplný binárny strom je taký binárny strom, ktorý má všetky úrovne okrem poslednej plné, a v poslednej sú všetky vrcholy natoľko vľavo, nakoľko sa to pri ich počte dá.

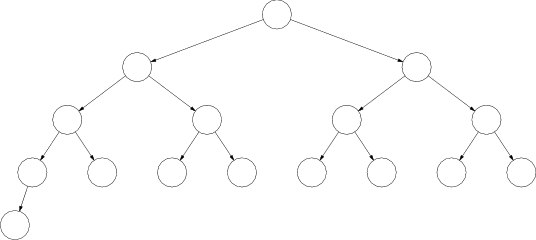
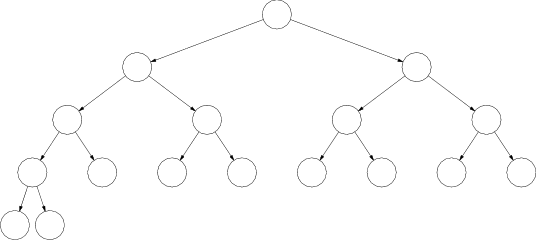
Zjavne pre každé $n$ existuje práve jeden takmer úplný binárny strom s $n$ vrcholmi. Ich konštrukciu môžeme popísať aj takto: Takmer úplný strom s $n>1$ vrcholmi zostrojíme z takmer úplného stromu s $n-1$ vrcholmi tak, že nájdeme najmenšiu úroveň, do ktorej sa dá pridať vrchol, a pridáme ho do nej na najľavejšie možné miesto.

Tiež si všimnite, že pre každé $n$ z množiny ${ 2^k, 2^k + 1, \dots, 2^{k+1} - 1 }$ má $n$-vrcholový takmer úplný binárny strom hĺbku $k$. Toto isté môžeme povedať aj nasledovne: Takmer úplný binárny strom s $n$ vrcholmi má hĺbku $\lfloor \log_2 n \rfloor$.

Binárna halda

Tak, a sme tu. Po všetkej príprave si konečne ideme vyrobiť konkrétnu vlastnú haldu. A určite už tušíte, ako na to pôjdeme: naša halda (odborne nazývaná binárna halda) bude mať tvar takmer úplného binárneho stromu.

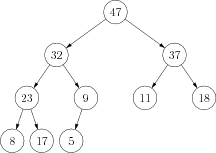
Veľkou výhodou binárnej haldy je, že ju vieme ľahko implementovať bez použitia ukazovateľov (pointrov). Stačí nám jedno dostatočne veľké pole. Haldu doň uložíme "po riadkoch". Teda na začiatku poľa bude uložený koreň, za ním zľava doprava jeho synovia, za nimi zľava doprava ich synovia, a tak ďalej.

index |  0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 |  9 | 
------+----+----+----+----+----+----+----+----+----+----+--
prvok | 47 | 32 | 37 | 23 |  9 | 11 | 18 |  8 | 17 |  5 |

Všimnite si, že $n$-prvková binárna halda nám zaberá presne prvých $n$ pozícii v poli. Ak majú prvky v poli indexy 0 až $n-1$, tak platia nasledovné vlastnosti:

• Otec vrcholu s indexom $x$ má index $\lfloor (x-1)/2\rfloor$.
• Synovia tohoto vrcholu majú indexy $2x+1$ a $2x+2$.

Ku každému vrcholu teda vieme jeho otca aj prípadných synov nájsť v konštantnom čase. Vďaka tomuto nepotrebujeme žiadne pointre, aj bez nich vieme priamo s poľom pracovať tak, ako by sme pracovali s haldou reprezentovanou ako strom.

Výber maxima z binárnej haldy

Vo všeobecnosti môžeme pri výbere z haldy odstrániť ľubovoľný list. Konkrétne pri výbere z binárnej haldy však máme úplne jasnú voľbu: vždy odstránime najpravejší list na najspodnejšej úrovni, teda ten, ktorý je v našom poli uložený na pozícii $n-1$. Odstránením tohto listu totiž opäť vznikne takmer úplný binárny strom.

Pri našej implementácii sa teda udeje nasledovné:

1. Prvok z koreňa (index 0) presunieme do pomocnej premennej.
2. Prvok z indexu $n-1$ presunieme na index 0.
3. Pole o jednu pozíciu zmenšíme. (Presnejšie, nespravíme nič, len sa budeme odteraz tváriť, že je naše pole o jedno kratšie.)
4. Prvok z indexu 0 postupne prebubleme dodola na nejakú pozíciu, na ktorú patrí.

Efektívnosť binárnej haldy

Pri vkladaní prvku nový prvok pridáme do najspodnejšej vrstvy a následne ním prebubleme dohora. Čas potrebný na vloženie prvku je teda v najhoršom prípade priamo úmerný hĺbke haldy.

Keďže v binárnej halde má každý vrchol najviac dvoch synov, vieme pravidlo bublania dodola použiť na ľubovoľný vrchol v konštantnom čase. Celý výber maxima teda tiež vieme spraviť v čase, ktorý je v najhoršom prípade priamo úmerný hĺbke haldy.

No a tu sa ukazuje, prečo bolo dobré zvoliť si práve binárnu haldu. Binárna halda s $n$ prvkami má tvar takmer úplného binárneho stromu, a teda má hĺbku rovnú $\lfloor\log_2 n\rfloor$.

Preto majú obe operácie "vloženie prvku do binárnej haldy" a "výber najväčšieho prvku z nej" časovú zložitosť $O(\log n)$.

Implementácia

Vo väčšine programovacích jazykov haldu nájdeme v štandardných knižniciach. Netreba teda programovať vlastnú, stačí použiť existujúcu. Napr. v C++ máme dátovú štruktúru priority_queue a v Pythone máme funkcie heappush a heappop v module heapq.

My si však ukážeme celú implementáciu haldy. Ak vám nejaké detaily neboli jasné, skúste si prejsť program a pozrieť sa, ako funguje.

class heap {
    public:
        void push(int);
        int pop();
    private:
        vector<int> data;
};

void heap::push(int what) {
    data.push_back(what);
    int where = data.size() - 1;
    while (where > 0) {
        int parent = (where-1)/2;
        if (data[where] > data[parent]) {
            swap( data[where], data[parent] );
            where = parent;
        } else {
            break;
        }
    }
}

int heap::pop() {
    int n = data.size();
    int answer = data[0];
    swap( data[0], data[n-1] );
    data.pop_back();
    int where = 0;
    while (true) {
        int dest = where;
        if (2*where+1 < n-1 && data[2*where+1] > data[dest]) dest = 2*where+1;
        if (2*where+2 < n-1 && data[2*where+2] > data[dest]) dest = 2*where+2;
        if (dest != where) {
            swap( data[where], data[dest] );
            where = dest;
        } else {
            return answer;
        }
    }
}

Bonus 1: Tvorba binárnej haldy z neusporiadaného poľa

Vyrobiť haldu obsahujúcu daných $n$ prvkov vieme aj efektívnejšie ako postupným vkladaním prvkov do pôvodne prázdnej haldy. Použitím jednoduchého triku dokážeme binárnu haldu vyrobiť v lineárnom čase.

Majme pole obsahujúce našich $n$ prvkov. Na toto pole sa môžeme dívať ako na takmer úplný binárny strom, v ktorom len potrebujeme preusporiadať prvky tak, aby všade platila podmienka haldy. Ukážeme, že na to, aby sme ju zabezpečili, stačí v správnom poradí bublať jej prvkami dodola.

Presnejšie, budeme prvky spracúvať od konca poľa, t. j. od listov haldy. Pre každý z nich zoberieme hodnotu, ktorá v ňom aktuálne je, a prebubleme ňou dodola, kým to ide.

Prečo to funguje?

Stačí si všimnúť, že vždy v okamihu, kedy spracujeme niektorý vrchol, platí, že celý podstrom daného vrcholu už spĺňa podmienku haldy. (Keď spracúvame nejaký vrchol, znamená to, že už sme predtým spracovali oboch jeho synov, a teda ich podstromy už oba spĺňajú podmienku haldy. Máme teda starú známu situáciu, kedy jedine hodnota v koreni aktuálneho podstromu kazí podmienku haldy v ňom, no a bublaním tejto hodnoty dodola tento kaz odstránime.)

A zaujímavejšia otázka: Ako rýchlo to funguje?

Celkovú časovú zložitosť vieme odhadnúť ako počet spracovaných vrcholov plus celkový počet krokov bublania dodola. Počet spracovaných vrcholov je $n$. Celkový počet krokov bublania dodola odhadneme nasledujúcou úvahou:

Predstavme si, že sme nechali prebehnúť náš algoritmus. Všimnime si teraz ľubovoľnú konkrétnu úroveň $x$ v našej halde a položme si otázku: Koľkokrát sa stalo, že na túto úroveň klesol niektorý prvok?

Zjavne keď pre každú úroveň spočítame počet prvkov, ktoré na ňu niekedy klesli, dostaneme presne celkový počet krokov bublania dodola.

No a na druhej strane na úroveň $x$ mohli klesnúť len prvky, ktoré pôvodne boli na vyšších úrovniach. A tých bolo presne $2^x - 1$.

Preto celkový počet krokov bublania dodola v halde s hĺbkou $k$ je nanajvýš rovný $$ (2^k - 1) + (2^{k-1}-1) + \cdots + (2^1 - 1) = 2^{k+1} - k - 2 $$

No a pre počet vrcholov $n$ haldy s hĺbkou $k$ platí $n\geq 2^k$. A teda celkový počet krokov bublania dodola je menší ako $2n$.

Bonus 2: Zložitejšie haldy

Existujú aj zložitejšie haldovité dátové štruktúry, ktoré vedia efektívne robiť všetky operácie, ktoré vie "klasická" binárna halda, a niečo naviac. Prvým príkladom je binomická halda. Nejde vlastne o haldu podľa našej definície, ale o množinu obsahujúcu niekoľko háld špeciálneho tvaru, pričom počty vrcholov v nich sú navzájom rôzne mocniny dvoch. Oproti binárnej halde vie binomická halda navyše operáciu merge: vieme v čase $O(\log n)$ spojiť dve binomické haldy do jednej.

Ešte komplikovanejšou dátovou štruktúrou je Fibonacciho halda, ktorá vie robiť niektoré operácie (vloženie prvku, spojenie dvoch háld a zvýšenie priority danému prvku) dokonca v amortizovanom konštantnom čase. Implementácia Fibonacciho haldy je komplikovaná. V praxi sa len zriedka stretneme s natoľko veľkými vstupmi, aby sa lepšia asymptotická časová zložitosť Fibonacciho haldy prejavila. Táto dátová štruktúra však má veľký význam v teoretickej oblasti pri návrhu nových efektívnych algoritmov.

Riešenia cvičení

Cvičenie 1

• Druhý najväčší prvok sa musí nachádzať bezprostredne pod koreňom, čiže v jednom z jeho synov.
• Tretí najväčší prvok môže byť tiež synom koreňa, taktiež ale môže byť synom druhého najväčšieho prvku.
• Najmenší prvok musí byť v niektorom z listov.
• Druhý najmenší prvok tiež môže byť v liste, je však ešte jedna možnosť: môže sa stať, že druhý najmenší prvok je vo vrchole, ktorý má práve jedného syna: najmenší prvok.

Všimnite si ten rozdiel medzi množstvom informácie, ktorú máme na rôznych koncoch spektra. O najväčšom prvku vieme presne, kde sa nachádza. Ďalšie veľké prvky sú niekde v jeho bezprostrednom okolí. Na druhej strane o najmenších prvkoch nevieme skoro nič.

(Napríklad v binárnej maximovej halde, ktorá je v texte popísaná neskôr, je 6 možností pre polohu tretieho najväčšieho prvku, zatiaľ čo až zhruba $3n/4$ možností pre polohu tretieho najmenšieho.)

Cvičenie 2

Počas prvých troch krokov nášho algoritmu sme prvok, ktorý je teraz vo vrchole $x$, postupne vymenili s prvkami $p_1$, $p_2$ a $p_3$. Tieto boli pôvodne na nejakej ceste dole haldou, preto platilo $p_1 \geq p_2 \geq p_3$. Priamo pod $p_3$ bol doteraz prvok, ktorý je vo vrchole $y$. No a práve ten istý prvok teraz nasledujúcou výmenou vrátime späť pod $p_3$. Preto pri výmene prvkov vo vrcholoch $x$ a $y$ nad sebou podmienku haldy nikdy neporušíme.