Keď si Baklažán nedávno vychutnával tabuľku svojej obľúbenej čokolády, objavil v nej zlatý lístok, ktorý mu garantoval návštevu Wonkovej továrne na čokoládu. So skupinou ďalších detí sa nadšený vydal do útrob obrovského komplexu. A že ho tam čakalo prekvapení – spievajúci trpaslíci, veveričky lúskajúce orechy, žuvačky každej chuti, riečna sieť tečúcej čokolády…
Deti, ktoré našli zlatý lístok sú však rozmaznané, nenásytné, pyšné a Willimu Wonkovi lezú poriadne na nervy. A Baklažán tomu tiež veľmi nepomáha, občas totiž odmieta pochopiť, čo sa mu snažíte povedať. Preto keď už tretíkrát odpovedal na Willyho otázku, či chce jahodovú alebo malinovú čokoládu, áno, Willy sa nahneval a zhodil ho do burácajúcej čokoládovej rieky.
Baklažán sa však tak ľahko nevzdáva. Rozhodol sa doplávať na ďaľšiu zastávku Wonkovej exkurzie. Otázka však je, či to stihne. Každý úsek riečnej siete je síce rovnako dlhý, tečie v ňom však rôzne hustá čokoláda. Platí, že preplávanie úseku s hustotou \(w\) bude Baklažánovi trvať čas \(w\). Jeho cieľom je dostať sa na plánované miesto stretnutia čo najrýchlejšie.
Plávanie v čokoláde má však ešte jednu veľkú (ne)výhodu. Chcete ochutnať každý druh čokolády, v ktorej plávate. Baklažán vie, že ak ochutná viac ako \(c\) čokolád, dostane hyperglykemický šok a do cieľa už nedopláva. Môže teda preplávať cez najviac \(c\) úsekov. Naviac, plávanie s plným bruchom je čoraz ťažšie a ťažšie. Chcel by preto, aby hustota čokolád, v ktorých pláva, celý čas stúpala, aby sa mu plávalo ľahšie1.
Úloha
Riečnu sieť tečúcej čokolády si môžete predstaviť ako graf, ktorý má \(n\) vrcholov (očíslovaných od 1 po \(n\)) a \(m\) orientovaných hrán. Každá hrana predstavuje jeden úsek rieky a má priradené číslo \(w_i\) – hustotu daného úseku. Platí, že na preplávanie úseku s hustotou \(w_i\) je potrebný čas \(w_i\).
Vaše riešenie musí odpovedať na \(q\) otázok. Každá otázka je tvorená troma celými číslami \(a_i\), \(b_i\) a \(c_i\) – ako najrýchlejšie sa vie Baklažán dostať z vrcholu \(a_i\) do vrcholu \(b_i\), ak môže preplávať cez najviac \(c_i\) úsekov a hustoty úsekov musia počas celej plavby stúpať?
Formát vstupu
Prvý riadok vstupu obsahuje tri celé čísla \(n\), \(m\) a \(q\) (\(2 \leq n \leq 150\), \(0 \leq m \leq 3\,000\), \(1 \leq q \leq 1\,000\)) – počet vrcholov a hrán grafu a počet otázok, na ktoré musíte odpovedať.
Nasledujúcich \(m\) riadkov popisuje hrany grafu. Každá hrana je popísaná troma číslami \(x_i\), \(y_i\) a \(w_i\). Táto trojica reprezentuje orientovanú hranu z vrchola \(x_i\) do vrchola \(y_i\) s hustotou \(w_i\). Medzi dvojicou vrcholov môže viesť aj viacero hrán, dokonca aj v tom istom smere. Platí, že \(1 \leq x_i, y_i \leq n\) a \(1 \leq w_i \leq 3\,000\). Naviac, žiadne dve hrany nemajú rovnakú hustotu \(w_i\).
Každý z nasledujúcich \(q\) riadkov obsahuje tri čísla \(a_i\), \(b_i\) a \(c_i\), ktoré popisujú otázky, na ktoré máte odpovedať – ako najrýchlejšie sa vie Baklažán dostať z vrchola \(a_i\) do vrchola \(b_i\) ak môže použiť najviac \(c_i\) hrán, ktorých hustoty postupne stúpajú? Pre každú otázku platí, že \(1 \leq a_i \neq b_i \leq n\) a \(0 \leq c_i \leq m\).
Úloha má 8 sád testovacích vstupov. Pre jednotlivé sady navyše platia nasledovné obmedzenia:
| číslo sady | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) a \(8\) |
|---|---|---|---|---|---|---|---|
| \(n \leq\) | \(8\) | \(20\) | \(20\) | \(50\) | \(50\) | \(150\) | \(150\) |
| \(q \leq\) | \(1\) | \(1\) | \(1000\) | \(1\) | \(1000\) | \(1\) | \(1000\) |
Formát výstupu
Pre každú otázku vypíšte na samostatný riadok odpoveď v poradí, v akom sa otázky objavili na vstupe. Pokiaľ Baklažán nevie splniť zadanie niektorej otázky, vypíšte -1.
Príklady
Input:
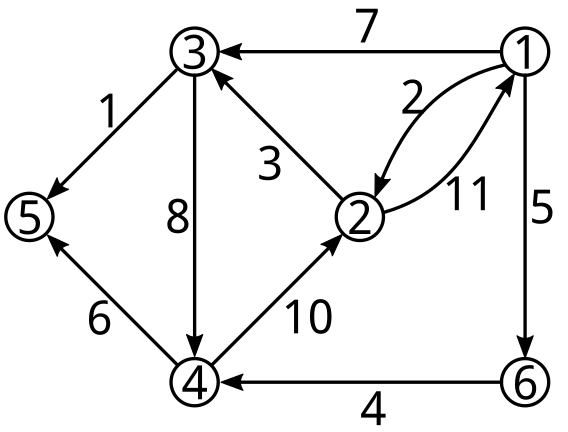
6 10 3
1 2 2
2 1 11
2 3 3
1 3 7
1 6 5
6 4 4
4 5 6
3 5 1
4 2 10
3 4 8
1 4 2
1 4 3
2 5 5Output:
15
13
-1Ak sa chceme dostať z vrchola 1 do vrchola 4 použitím najviach dvoch hrán, máme iba jednu možnosť, ísť cez vrchol 3. Cesta cez vrchol 6 totiž nespĺňa podmienku, že hustota hrán má postupne rásť.
Z vrchola 2 sa do vrchola 5 nevieme dostať bez toho aby sme neporušili podmienku zo zadania.
Niečo, niečo, fyzika, niečo, niečo, vztlak…↩
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.