2. Oštara s huncútmi malými

Ako tak študent Dávid cestou domov začal konzumovať čokoládu, jej úlomky dopadali na chodník. Na druhý deň išiel Dávid po tom istom chodníku, znova konzumujúc čokoládu a opäť mu zopár malých kúskov spadlo na zem. Táto situácia sa opakuje každý deň, lebo Dávid je svedomitý študent a zároveň veľký milovník čokolády.

Na začiatku tohto chodníka prebývajú mravce – bažiace po čokoláde, a mimochodom, mimoriadne expanzívne. Ak sa niekde v okolí mraveniska vyskytne kúsok čokolády, mravce neváhajú a rozšíria svoje mravenisko až po tento kúsok. Ak teda Dávid bude pokračovať vo svojom zvyku konzumovať čokoládu cestou zo školy, mravce časom skolonizujú celý chodník.

Dávid by ale nerád (nevedomky) predal našu krajinu mravcom. Keď od vás dostane každý deň údaj o tom, kde sa nachádza hranica mravčej ríše, uvedomí si vážnosť celej situácie a podnikne rázne protiopatrenia.

Úloha

Chodník má dĺžku \(n+1\) metrov. Môžeme si ho teda predstaviť ako časť číselnej osi od bodu \(0\) po bod \(n+1\). Zo začiatku je celé mravenisko v bode \(0\). Neskôr sa bude rozširovať na čoraz dlhší interval na chodníku.

Rozpínavosť mravcov sa dá charakterizovať kladným číslom \(v\) s nasledovným významom: ak sa niekedy vo vzdialenosti \(v\) alebo menej metrov od mraveniska nachádza kúsok čokolády, mravce ho pohltia a tak rozšíra svoje impérium až po tento kúsok. Ako pracovité tvory sú toto schopné urobiť v rámci jedného dňa ľubovoľne veľa ráz – posunutím hranice sa totiž môže stať, že mravce už ,,dočiahnu’’ aj na ďalšie kúsky čokolády, na ktoré predtým nedočiahli. Navyše, ak sa niekedy dostanú do vzdialenosti \(v\) alebo menej metrov od konca chodníka, rozšíria sa až po koniec chodníka (teda akoby na konci chodníka bola čokoláda).

Dávid má zvláštny talent na trúsenie čokolády. Po prvé, čokoládové omrvinky mu padajú iba na miesta, ktoré sú celočíselný počet metrov od začiatku chodníka. Okrem toho Dávidovi nikdy nepadne omrvinka dvakrát na to isté miesto. Zároveň však platí, že na všetky body \(1, 2, \dots, n\) mu časom nejaká omrvinka padne.

Kým sa mravce dostanú po koniec chodníka v bode \(n+1\), zopár dní im to potrvá. Vašou úlohou bude zistiť, kde sa bude nachádzať hranica mravčieho impéria po jednotlivých dňoch expanzie, až kým neskolonizujú celý chodník.

Formát vstupu

Na prvom riadku vstupu sa nachádzajú dve celé čísla \(n\) (\(2 \leq n \leq 100\,000\)) a \(v\) (\(1 \leq v \leq 100\,000\)) – počet omrviniek, ktoré Dávid vytrúsi, a expanzívnosť mravcov. Nasleduje \(n\) riadkov popisujúcich jednotlivé kúsky čokolády, ktoré Dávid vytrúsil. Každý z týchto riadkov obsahuje dve celé čísla \(m_i\) (\(1 \leq m_i \leq n\)) a \(d_i\) (\(0 \leq d_i \leq 100\,000\)) – pozíciu danej omrvinky a číslo dňa, keď táto omrvinka spadne. Dni číslujeme od nuly.

Môžete predpokladať nasledovné:

1. Kúsky čokolády budú na vstupe zoradené vzostupne podľa dňa, kedy padli. Viacero kúskov mohlo padnúť v rovnaký deň – na vstupe sa vtedy objaví skôr ten, ktorý padol na skorší meter chodníka.

2. Na každý meter chodníka medzi \(1\) a \(n\) (vrátane) padne práve jeden kúsok čokolády.

Keďže expanzívnosť mravcov je aspoň \(1\), určite sa časom dostanú až na koniec chodníka.

Riešenia, ktoré zvládnu riešiť iba prípady kde \(\boldsymbol{v = 1}\), získajú v praktickom testovaní približne polovicu bodov a môžu získať až polovicu bodov za popis.

Formát výstupu

Deň, počas ktorého sa mravce dostanú na koniec chodníka, označme \(c\). Vypíšte \(c+1\) čísel – na koľkom metri sa nachádzala hranica mraveniska na konci dňa \(0, 1, 2, 3, ..., c\). Každé číslo nech je na samostatnom riadku.

Príklady

Input:

6 1
1 2
3 2
5 2
2 3
4 4
6 4

Output:

0
0
1
3
7

V dňoch \(0\) a \(1\) nepadla žiadna čokoláda, mravce teda tieto dva dni ostanú na začiatku chodníka. Počas dňa \(2\) padne na meter \(1\) čokoláda, ktorú mravce pohltia. Hoci v ten istý deň padla omrvinka aj na metre \(3\) a \(5\), mravce ich nepohltia, pretože ich expanzívnosť je len \(1\). Počas dňa \(3\) padne čokoláda na meter \(2\) a vtedy mravce pohltia ďalšie \(2\) metre. Po ďalšom dni už budú schopné ovládnuť celý chodník.

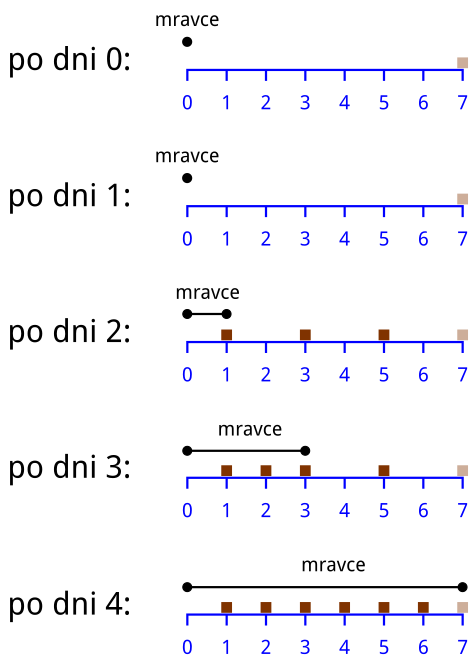
Input:

6 3
1 0
2 1
3 1
6 1
5 6
4 8

Output:

1
7

Na prvý meter padla čokoláda hneď, preto už od začiatku bude ríša hraničiť na prvom metri. Ďalší deň padne jedlo na metre \(2\), \(3\), \(6\). Kedže tieto body sú dostatočne blízko seba (aj bodu \(7\)), mravce rovno ovládnu všetko.