8. Automat

V Erikovej škole majú automat na čokoládové tyčinky. Taký klasický automat: vhodíte peniaze, vyberiete si, akú tyčinku chcete, a automat vám ju vydá.

Nedávno sa však automat pokazil, takže väčšinou vám okrem tyčinky, ktorú ste si vybrali, vysype aj nejaké ďalšie. Erik, súc charakterný mladý muž, túto poruchu ihneď nahlásil a prestal automat používať. Keďže je však Erik zároveň aj od prírody veľmi zvedavý, napadla mu jedna hypotetická otázka: koľko by toho dokázal z automatu vytiahnuť za peniaze, ktoré má práve pri sebe?

Úloha

Automat predáva \(n\) rôznych druhov tyčiniek, očíslovaných \(1\) až \(n\). Z každého druhu je v automate niekoľko kusov a každý druh má nejakú cenu (rôzne druhy môžu mať rôzne ceny). Ak si v automate kúpite tyčinku druhu \(x\), automat vám navyše vydá po jednej tyčinke z druhov \(1, 2, \dots, x-1\) (ak ešte nejaké má. Ak z nejakého druhu už nemá žiadnu tyčinku, jednoducho vám z tohto druhu nevydá nič). Ak automatu dôjdu tyčinky nejakého druhu, prestane tento druh predávať (takže tyčinky tohto druhu sa už nedajú kúpiť).

Erik má momentálne pri sebe \(k\) centov. Aká je najväčšia možná celková hodnota tyčiniek, ktoré Erik dokáže ,,kúpiť’’ z automatu za peniaze, ktoré má?

Formát vstupu

V prvom riadku vstupu sú dve medzerou oddelené celé čísla \(n, k\) (\(1 \leq n \leq 50\), \(1 \leq k \leq 200\,000\)) – počet druhov tyčiniek a množstvo peňazí, ktoré má Erik k dispozícii.

Druhý riadok obsahuje \(n\) medzerami oddelených celých čísel \(c_1, c_2, \dots, c_n\) (\(1 \leq c_i \leq 50\)), kde \(c_i\) je cena \(i\)-teho druhu tyčiniek.

Tretí riadok obsahuje \(n\) medzerami oddelených celých čísel \(p_1, p_2, \dots, p_n\) (\(0 \leq p_i \leq 50\)), kde \(p_i\) je počiatočný počet tyčiniek \(i\)-teho druhu.

Formát výstupu

Vypíšte jeden riadok obsahujúci jedno celé číslo: najväčšiu možnú hodnotu tyčiniek, ktoré dokáže Erik získať s peniazmi, ktoré má.

Príklady

Input:

5 30
15 25 10 50 5
3 6 3 5 2

Output:

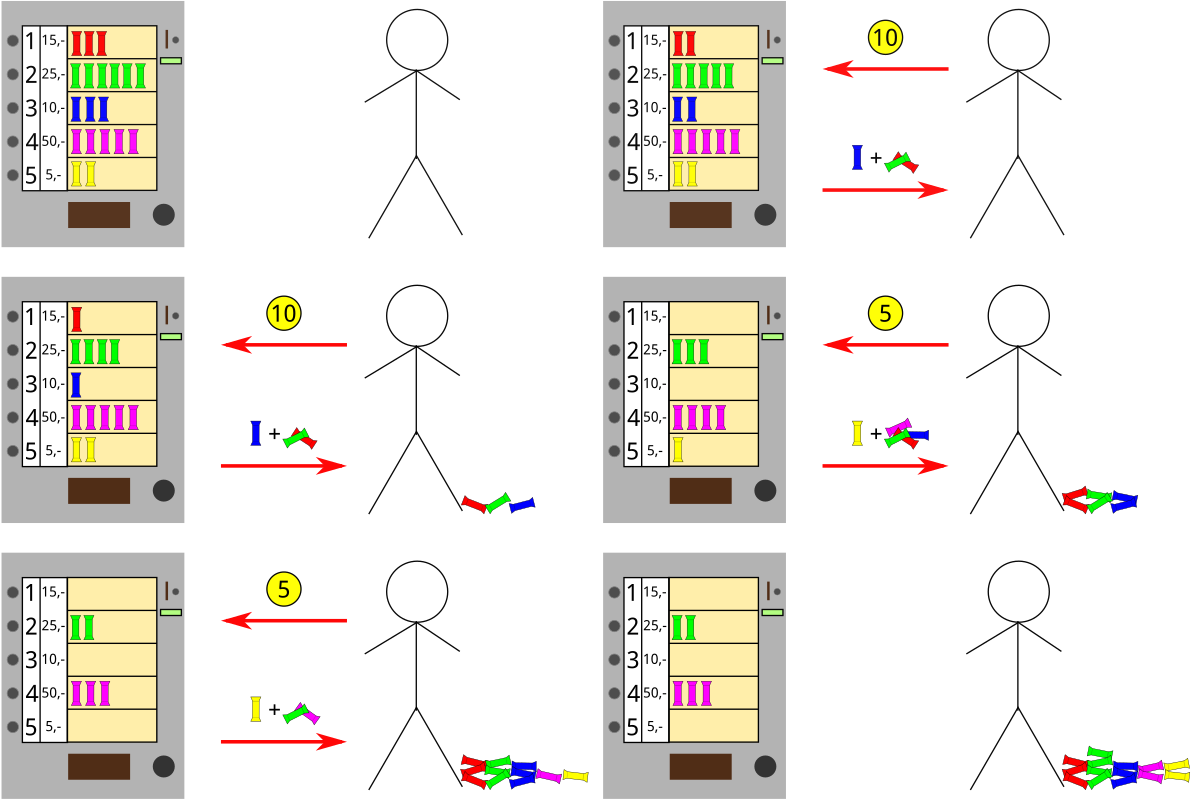
285

Erik najprv za 20 centov kúpi dve tyčinky 3. druhu (pričom mu z automatu vypadnú aj po dve tyčinky 1. a 2. druhu). Následne kúpi dve tyčinky 5. druhu. Pri nákupe prvej z nich dostane aj po jednej tyčinke z prvých štyroch druhov, pri nákupe druhej z nich dostane tyčinku 2. a 4. druhu (tyčinky 1. a 3. druhu sa už minuli). Nakoniec má teda Erik 3 tyčinky 1. druhu, 4 tyčinky 2. druhu, 3 tyčinky 3. druhu, a po 2 tyčinky 4. a 5. druhu.