4. Ovce v Koloseu ?!

Ráno bitka, na obed bitka, poobede bitka, večer bitka. Napriek tomu, že sledovať súboj gladiátorov na život a na smrť¹ vie byť pomerne zábavný spôsob ako premárniť zopár hodín voľného času², takýto program miestny ľud rýchlo omrzel.

Cézar dal teda po krajine rozhlásiť, že sa plánuje spestrenie vystúpení v Koloseu – organizuje sa prvý ročník šou Rímska ríša má talent!. Prvé oficiálne kolo bude už o mesiac priamo v Koloseu – a rozhodovať bude samotný cézar.

Farmárovi Denisiovi sa splnil sen. Konečne bude môcť zažiariť a ukázať, čo sa v ňom skrýva. Doteraz sa v Koloseu nemal čím predvádzať – na gladiátorské súboje bol príliš chudý a slabý. Ale s ovcami, s tými si teda rozumie.

Dlhé roky ich vyháňal na pašu a vo voľnom čase ich učil rôzne cirkusové kúsky. Je si však vedomý, že konkurencia bude veľká – už sa šíria chýry o cestujúcom, ktorý vie chodiť po vode. Aby mal šancu na víťazstvo, musí si Denisius nechať svoje najúžasnejšie ovčie kúsky na neskoršie kolá súťaže. Najlepšie by bolo, keby sa do ďalšieho kola dostal s najmenej nacvičeným trikom – ovce priučil jednoduchej geometrii a na jeho povel sa chaotické stádo oviec razom rozostaví na najviac dve priamky.

Pred svojim vystúpením by si chcel tento kúsok so svojimi ovcami ešte precvičiť – ak sa mu nevydarí, určite nepostúpi, a to ho potom cézar dá zožrať levom³. Z hľadiska Kolosea sa výkon jeho oviec hodnotí ľahko, keď však Denisius stojí spolu s ovcami na lúke za dedinou, nevidí, či sa jeho ovce naozaj poslušne postavili na najviac dve priamky. Na to potrebuje vašu pomoc!

Úloha

V Denisiovom stáde je \(n\) oviec. Každú ovcu si môžeme predstaviť ako bod v rovine s celočíselnými súradnicami. Dostanete rozostavenie oviec po tom, čo Denisius zadal povel, aby sa postavili na najviac dve priamky. Zistite, či sa im to podarilo.

Formát vstupu

V prvom riadku je celé číslo \(n\) (\(1 \leq n \leq 2 \cdot 10^5\)) – počet oviec v Denisiovom stáde.

V nasledujúcich \(n\) riadkoch sú po dve celé čísla \(x_i, y_i\) – súradnice \(i\)-tej ovce po tom, čo Denisius dal svoj povel.

Súradnice v absolútnej hodnote neprekročia \(10^9\). Žiadne dve ovce nestoja na rovnakých súradniciach.

Sú štyri sady testovacích vstupov. Maximálne hodnoty \(n\) v jednotlivých sadách sú nasledovné:

Formát výstupu

Ak existujú dve priamky také, že každá ovca stojí aspoň na jednej z nich, vypíšte ANO. Inak vypíšte NIE.

Príklady

Input:

6
0 1
3 4
10 11
5 0
6 2
8 6

Output:

ANO

Prvé tri ovce stoja na jednej priamke, posledné tri na druhej:

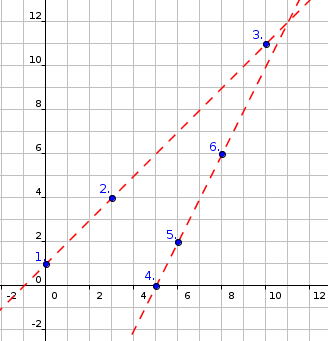
Input:

6
0 1
3 4
9 11
5 0
6 2
8 6

Output:

NIE