Istej nemenovanej firme sa ako prvej podarilo vyvinúť teleportujúce zariadenie. To vykonáva takú činnosť, že vezme objekt na jednej stanici, rozseká ho na atómy, tie pošle na druhú stanicu, a tam z atómov objekt napäť poskladá. Už má v krajine nainštalovaných viacero takýchto párov teleportov, a každý pár umožňuje rýchlo cestovať zo zdrojového mesta do cieľového mesta (ale nie opačným smerom).
Človek by očakával, že za použitie teleportu je potrebné zaplatiť, tak ako pri iných dopravných prostriedkoch. Pri niektorých pároch teleportov sa ale firma rozhodla, že za ich použitie cestujúcemu zaplatí, aby tak podporila používanie teleportov a aby ľudia prekonali počiatočnú nedôveru v tento spôsob dopravy.1
Takto ľahko zarábať peniaze, no kto by to neodmietol? Buj teda určite nie. Má to ale jedno obmedzenie – podľa firmy je za jeden deň bezpečné použiť teleport iba \(k\)-krát.
Aby si Buj vedel svoju cestu naplánovať, potrebuje pre každú dvojicu miest zistiť, koľko najviac peňazí môže zarobiť (alebo koľko najmenej musí zaplatiť), ak sa chce dostať z prvého mesta do druhého použitím najviac \(k\) teleportov.
Úloha
Zadaný je orientovaný graf s ohodnotenými hranami, a kladné celé číslo \(k\). Pre každú usporiadanú dvojicu vrcholov zistite, či existuje sled dĺžky najviac \(k\) začínajúci v prvom vrchole a končiaci v druhom. Ak áno, tak zistite, aký najväčší súčet hodnôt hrán môže mať taký sled.
Formát vstupu
Na prvom riadku vstupu sú tri celé čísla: počet vrcholov grafu \(n\) (\(\geq 1\)), počet hrán grafu \(m\) (\(\geq 0\)) a číslo \(k\) (\(\geq 0\)) s rovnakým významom, ako je uvedené vyššie.
Nasleduje \(m\) riadkov, každý z nich popisuje jednu hranu grafu. Pozostáva z troch celých čísel \(a, b, h\) oddelených jednou medzerou, hovoriacich, že v grafe sa nachádza hrana z vrcholu \(a\) do \(b\) s hodnotou \(h\). Platí \(1 \leq a, b \leq n\) (\(a\) a \(b\) môžu byť rovnaké), \(|h| \leq 10^9\), a pre každé dva (nie nutne rôzne) vrcholy platí, že existuje najviac jedna hrana vedúca z prvého vrcholu do druhého.
Obmedzenia
| Sada | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \(n \leq\) | \(10\) | \(17\) | \(31\) | \(56\) | \(100\) |
| \(k \leq\) | \(10\) | \(10^3\) | \(10^5\) | \(10^7\) | \(10^9\) |
Formát výstupu
Vypíšte tabuľku \(n \times n\) (teda \(n\) riadkov, a v každom riadku \(n\) políčok tabuľky oddelených medzerou). V \(i\)-tom riadku na \(j\)-tom políčku zľava nech je X, ak neexistuje sled z \(i\) do \(j\) dlhý najviac \(k\). Ak existuje, tak nech v tom políčku je číslo vyjadrujúce najväčší súčet hodnôt hrán spomedzi vyhovujúcich sledov.
Tieto čísla môžu byť veľké, preto tam, kde je to treba, použite \(64\)-bitový číselný typ (long long).
Príklady
Input:
4 4 3
1 2 -1
2 3 -1
3 4 -1
4 3 3Output:
0 -1 -2 -3
X 0 1 -2
X X 2 1
X X 5 2Graf z príkladu vyzerá takto:
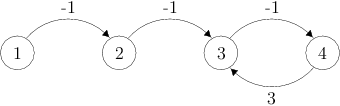
Existujú ale konšpiračné teórie, podľa ktorých iba zháňajú lacných testerov, alebo dokonca ovládnu myseľ používateľov tým, že ich mozog poskladajú inak.↩
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.