Nie je to tak dávno, čo sa do našej oválnej pracovne nasťahoval nový Týpek. Ako to už býva zvykom, nový týpek – nové nápady. A tak hneď ako ho napadol ten najlepší, zvolal svojich poradcov do oválnej pracovne. Za okrúhlym stolom im predostrel ideu postavenia veľkého múru pred nepriateľmi. Ako ale istá americká štúdia ukázala: čím bývajú nepriatelia viac na východ, tým sú nebezpečnejší. Preto musí byť múr na východe vyšší, alebo aspoň rovnako vysoký ako na západe.
Po nekonečných rokovaniach sa všetci v oválnej pracovni zhodli, že naša krajina je v ohrození a treba začať so stavbou ihneď. Ešteže zostalo v oválnej pracovni pod stolom zopár betónových stĺpov jednotkovej šírky. Stavbu teda môžeme zahájiť, no tak ako to pri veľkých projektoch býva potrebujeme plán, ten najlepší plán.
Hoci postavenie múru nie je vôbec populistické, zlé jazyky nás môžu začať ohovárať, preto musí mať náš múr aj nejaký hlboký zmysel, napríklad umelecký. Aby sme teda pred svetom nevyzerali ako barbari, musí sa postaviť múr esteticky, teda tak, aby rozdiel výšok medzi ľubovoľnými susednými betónovými stĺpmi bol rovnaký. Okrem toho je tu už spomínaný fakt, že nepriatelia na východe sú nebezpečnejší. Preto musia výšky jednotlivých stĺpov v múre tvoriť od západu na východ neklesajúcu postupnosť.
Na obrázku môžete vidieť päť rôznych múrov.
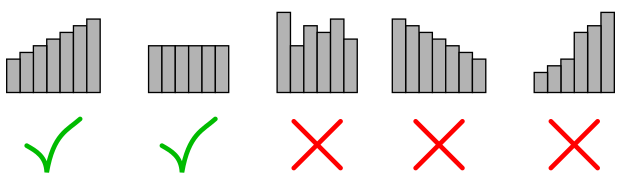
Prvé dva z nich sú dobré. Tretí je zlý, pretože výšky stĺpov netvoria neklesajúcu postupnosť. Štvrtý tak isto (tam stĺpy tvoria klesajúcu postupnosť). Piaty múr je zlý, lebo rozdiely medzi výškami susedných stĺpov nie sú všade rovnaké.
Pomôžte zachrániť krajinu pred čo najviac nepriateľmi a navrhnite čo najdlhší múr z materiálov, ktoré sú k dispozícií.
Úloha
Máme \(n\) betónových stĺpov s danými výškami. Zistite najväčšiu možnú dĺžku (počet použitých stĺpov) neklesajúceho múru ktorý vieme postaviť tak, aby v postavenom múre mali každé dva susedné betónové stĺpy rovnaký rozdiel výšok. Nemusíte použiť všetky stĺpy zo vstupu.
Formát vstupu
Na prvom riadku vstupu dostanete kladné celé číslo \(n\). V druhom riadku bude \(n\) medzerou oddelených nezáporných celých čísel \(a_1, a_2, ..., a_n\) reprezentujúcich výšky jednotlivých stĺpov.
Je päť testovacích sád. Pre jednotlivé sady platia nasledovné obmedzenia:
| číslo sady | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \(n \leq\) | \(20\) | \(100\) | \(500\) | \(1\,000\) | \(3\,000\) |
| \(a_i \leq\) | \(10^3\) | \(10^3\) | \(10^3\) | \(10^9\) | \(10^9\) |
Formát výstupu
Na výstup vypíšte jediné číslo – počet použitých stĺpov v najdlhšom možnom múre spĺňajúcom podmienky zo zadania.
Príklad
Input:
4
2 3 4 1Output:
4Zjavne dokážeme postaviť múr zo všetkých našich stĺpov a tiež splniť estetickú podmienku, stačí postaviť stĺpy v poradí 1, 2, 3, 4
Input:
5
2 1 5 2 4Output:
2Najdlhší múr vieme postaviť napríklad zo stĺpov výšok 2 a 4
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.