5. Tam, kde žijú algoritmy...

Bol raz jeden algoritmus, ktorého každodennou prácou bolo hľadanie najdlhšej cesty v strome s vrcholmi od \(1\) po \(n\). Jeho metóda bola nasledovná:

1. Strom si zakoreníme za vrchol s najmenším číslom.

2. Pre každého syna koreňa nájdeme najdlhšiu cestu, ktorej jeden koniec je samotný syn, a druhý koniec je v jeho podstrome. To spravíme obyčajným prehľadávaním do šírky.

3. Vyberieme dvoch synov s najdlhšími cestami. Keď tieto dve cesty prepojíme cez koreň, dostaneme najdlhšiu cestu prechádzajúcu koreňom.

4. Ešte sme ale nebrali do úvahy cesty, ktoré koreňom vôbec neprechádzajú. Každá taká cesta ale leží celá v podstrome niektorého syna. Stačí preto rekurzívne vyriešiť tieto podstromy – zakoreníme ich, spočítame pre synov koreňa najdlhšie cesty, …

Kolega programátor mu poradil, že ak by za koreň vždy zvolil centroid¹ (pod)stromu, tak by mal oveľa viac voľného času, lebo by vraj bežal v čase \(O(n \log {n})\) namiesto \(O(n^2)\).

Algoritmus sa nad tým zamyslel, a všimol si, že jeden strom môže mať viac ako jeden centroid. V takých prípadoch by sa musel rozhodnúť, ktorý z centroidov vybrať. S tým sa mu ale nechce otravovať. Zaujíma ho preto, koľko stromov s \(n\) vrcholmi je takých, že práca na ňom podľa nového postupu bude čisto manuálna, a nebude musieť počas nej robiť žiadne rozhodnutia.

Úloha

Strom je ľahký, ak má práve jeden centroid, a jeho odobratím sa strom rozpadne na niekoľko ľahkých stromov. Pre zadaný počet vrcholov \(n\) zistite, koľko rôznych stromov s \(n\) vrcholmi je ľahkých. (Dva stromy považujeme za rôzne, ak existujú vrcholy \(u, v\), ktoré sú hranou spojené v prvom strome, ale nie v druhom.) Toto číslo môže byť veľké, vypíšte preto jeho zvyšok po delení prvočíslom \(p\).

Formát vstupu

Na jedinom riadku vstupu sú dve celé čísla \(n, p\) oddelené medzerou. \(n\) udáva počet vrcholov a \(p\) je prvočíslo, po delení ktorým berieme zvyšok.

Je päť testovacích sád. Vo všetkých platí \(1 \leq n \leq 3\,000\), a \(n < p \leq 10^9\). Pre jednotlivé sady máme nasledovné obmedzenia:

Formát výstupu

Na jediný riadok výstupu vypíšte jedno celé číslo z \(\lbrace 0, 1, \ldots, p - 1 \rbrace\) – počet vyhovujúcich stromov s \(n\) vrcholmi, modulo \(p\).

Príklady

Input:

2 103

Output:

0

Pre \(n = 2\) existuje iba jeden strom:

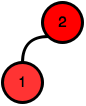
Tento strom nevyhovuje, nakoľko v prvom kroku môžeme za koreň zvoliť aj vrchol \(1\), aj \(2\).

Input:

4 103

Output:

4

Pre \(n = 4\) máme tieto štyri vyhovujúce stromy:

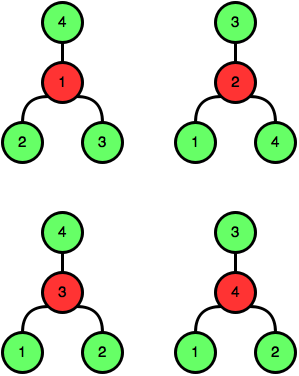
Príklad nevyhovujúceho stromu je

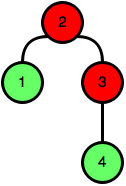
nakoľko môžeme v prvom kroku zvoliť za koreň \(2\) aj \(3\).