Máme vianočný stromček, ktorý vyzerá ako graf-strom. Na každom vrchole \(v\) je zavesená jedna ozdoba, označená celým číslom \(c_v\).
Občas sa pri stromčeku zastaví okoloidúci. Pozrie sa na cestu z vrcholu \(w\) do \(x\), ďalej sa pozrie na cestu z \(y\) do \(z\), a zamrmle, ako trápny sa mu zdá stromček na základe toho, čo videl. Úroveň trápnosti vypočíta ako počet usporiadaných dvojíc \((i, j)\) spĺňajúcich
\(i \neq j\)
Vrchol \(i\) leží na ceste z \(w\) do \(x\).
Vrchol \(j\) leží na ceste z \(y\) do \(z\).
Na oboch vrcholoch je zavesená rovnaká ozdoba, teda \(c_i = c_j\).
Úloha
Dostanete popis vianočného stromčeka. Následne príde \(q\) ľudí, a o každom vieme, na ktoré dve úseky sa pozrel. Pre každého zistite, akú úroveň trápnosti dáva stromčeku.
Formát vstupu
Prvý riadok obsahuje dve medzerou oddelené čísla \(n, q\) – počet vrcholov stromu a počet KSPákov.
Druhý riadok obsahuje \(n\) medzerou oddelených celých čísel \(c_1, c_2, \ldots, c_n\) – \(i\)-te z nich je ozdoba zavesená na \(i\)-tom vrchole.
Nasleduje \(n-1\) riadkov. Každý z nich obsahuje dve medzerou oddelené čísla \(u, v\) a popisuje hranu v strome medzi vrcholmi \(u\) a \(v\). Vrcholy sú číslované od \(1\) po \(n\).
Každý z nasledujúcich \(q\) riadkov obsahuje štyri medzerou oddelené čísla \(w, x, y, z\) s rovnakým významom, ako je uvedené vyššie.
Obmedzenia
Vo všetkých sadách platí
- \(1 \leq n \leq 100\,000\)
- \(1 \leq q \leq 50\,000\)
- \(1 \leq c_i \leq 10^9\)
- \(1 \leq u, v, w, x, y, z \leq n\)
Konkrétne obmedzenia pre jednotlivé sady sú
| Číslo sady | maximálne \(n\) | maximálne \(q\) |
|---|---|---|
| \(1\) | \(50\) | \(10\,000\) |
| \(2\) | \(300\) | \(300\) |
| \(3\) | \(5000\) | \(5000\) |
| \(4, 5\) | \(100\,000\) | \(50\,000\) |
Formát výstupu
Pre každého okoloidúceho vypíšte, akú úroveň trápnosti dáva stromčeku.
Príklady
Input:
10 5
10 2 3 5 10 5 3 6 2 1
1 2
1 3
3 4
3 5
3 6
4 7
5 8
7 9
2 10
8 5 2 10
3 8 4 9
1 9 5 9
4 6 4 6
5 8 5 8Output:
0
1
3
2
0Strom z príkladu vyzerá nasledovne:
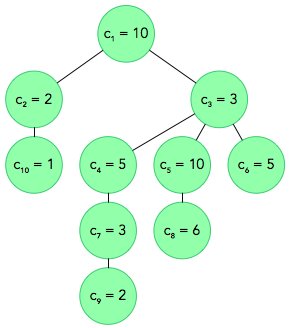
Prvý okoloidúci sa pozrie na úseky \(8 - 5\) a \(2 - 10\). Vrcholy v prvom úseku majú ale úplne iné ozdoby, ako tie v druhom úseku. Teda trápnosť je \(0\).
Druhý sa pozrie na úseky \(3 - 8\) a \(4 - 9\). Na vrchole \(3\) aj na \(7\) je zavesená ozdoba \(3\), takže trápnosť je \(1\).
Tretí sa pozrie na úseky \(1 - 9\) a \(5 - 9\). Dvojice vrcholov s rovnakými ozdobami sú \((1, 5)\), \((3, 7)\) a \((7, 3)\), teda vyhlási trápnosť \(3\).
Štvrtý sa pozrie dvakrát na ten istý úsek \(4 - 6\). Trápne dvojice sú \((4, 6)\) a \((6, 4)\), teda trápnosť je \(2\).
Piaty sa tiež dvakrát pozrie na ten istý úsek \(5 - 8\). V ňom majú ale všetky vrcholy rôzne ozdoby, takže trápnosť je \(0\).
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.