4. Zdobenie torty vzorové riešenie

Zadanie

Jankove narodeniny sa pomaly, ale isto blížia, a aby nebol taký smutný, že už bude starý, Peťka mu chce upiecť jahodovú tortu. Jediné, čo sa jej dosiaľ nepodarilo vymyslieť, je, ako tortu ozdobiť. Určite na ňu chce zvrchu poukladať \(n\) jahôd v pravidelných rozostupoch a pomedzi ne niečo nakresliť cukrovou polevou. Zatiaľ sa s ňou ale nenaučila robiť nič iné ako lomenú čiaru. Peťka preto chce tortu pokresliť lomenou čiarou, ktorá pôjde od jahody k jahode, medzi dvoma jahodami vždy len rovno. Nechce však, aby sa čiara kdekoľvek prekrížila sama so sebou, lebo by sa na tom mieste vytvoril cukrový hrboľ, čo je veľmi neestetické. Pomôžete jej zistiť, či sa čiara, ktorú naplánovala, prekríži?

Úloha

Pre zadaný kresliaci plán (čísla jahôd, medzi ktorými chce Peťka postupne nakresliť čiaru) má váš program rozhodnúť, či sa čiara niekde pretne sama so sebou. Je zaručené, že plán obsahuje každé číslo nanajvýš raz.

Formát vstupu

Na prvom riadku vstupu je kladné číslo \(t\) neprevyšujúce 30, určujúce počet plánov na vstupe. Každý plán je zadaný na dvoch riadkoch, pričom na prvom sú čísla \(n, m\) (\(2 \leq m \leq n \leq 200\,000\)), kde \(n\) udáva počet jahôd na torte a \(m\) udáva počet jahôd, medzi ktorými chce Peťka urobiť čiaru. Na druhom riadku sú čísla \(a_1, \dots, a_m\) (pričom \(1 \leq a_i \leq n\)), určujúce jahody, medzi ktorými chce Peťka postupne kresliť čiaru.

Pre polovicu vstupov platí \(n = m\) (teda ak viete rozhodnúť, či sa čiara pretne, len pre vstupy, kde čiara ide cez všetky jahody, môžete získať polovicu bodov).

Formát výstupu

Na výstup vypíšte \(t\) riadkov. Na \(i\)-tom má byť reťazec “PRETNE” (bez úvodzoviek) práve vtedy, keď sa čiara zadaná \(i\)-tym plánom zo vstupu pretne, inak má byť na \(i\)-tom reťazec “NEPRETNE” (bez úvodzoviek).

Príklad

Input:

2
8 6
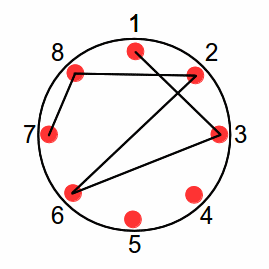
7 8 2 6 3 1
5 5
1 5 4 3 2

Output:

PRETNE
NEPRETNE

V prvom prípade môžete na obrázku vidieť, že pretnutie spôsobila posledná časť čiary od jahody 3 k jahode 1. V druhom prípade je jasné, že čiara sa nikde nepretne, pretože ide “po obvode” – iba medzi susednými jahodami.

Najprv sa zamyslíme nad tým, ako by sa príklad dal riešiť, keby čiara na torte išla cez všetky jahody. Jahodám, cez ktoré čiara počas kreslenia už prešla, budeme hovoriť pokreslené.

Keby sa nám počas kreslenia čiary na tortu niekedy stalo, že sme čiarou práve prišli k nejakej jahode, pričom aj naľavo aj napravo od tejto jahody je nepokreslená jahoda, je jasné, že plán sa už nebude dať dokončiť bez prekríženia čiary. (Ak by sme sa totiž v ďalšom kroku vybrali napravo od poslednej jahody, už sa nedostaneme k tej, čo je naľavo, bez toho, aby sa čiara prekrížila – a naopak analogicky.)

Túto myšlienku môžeme veľmi ľahko zovšeobecniť – pri kreslení čiary od jahody k jahode musí vždy platiť, že každá jahoda (okrem prvej), ku ktorej pôjdeme čiarou, má aspoň jednu z dvoch susedných jahôd už pokreslenú. To znamená, že počas kreslenia budeme mať vždy jeden súvislý úsek jahôd pokreslený a zvyšné jahody budú nepokreslené – teda pri každom ďalšom kuse čiary, ktorý budeme kresliť (okrem posledného), budeme mať na výber z dvoch jahôd – budú to tie nepokreslené, ktoré susedia s pokreslenými.

Program teda v tomto prípade funguje nasledovne: celý čas si bude pamätať interval pokreslených jahôd (na začiatku si ho inicializuje na prvú jahodu) a pri každom ďalšom kroku len skontroluje, či nová jahoda susedí s jednou z krajných jahôd intervalu, a ak áno, interval si príslušne zväčší. Ak nie, vyhlási, že plán je zlý a čiara sa pretne.

Čo ale v prípade, že plán neobsahuje všetky jahody? Keď venujeme chvíľku kresleniu rôznych plánov na papier, uvidíme, že z každej jahody sa môžeme pohnúť dvoma rôznymi smermi – doprava alebo doľava. Navyše, ak ideme vľavo, môžeme si vyberať len z tých jahôd vľavo, ktoré patria do nepokresleného intervalu začínajúceho ľavou susednou jahodou a končiaceho najbližšou pokreslenou jahodou. (Analogicky aj pre druhú stranu – ak ideme vpravo, môžeme ísť len na takú jahodu, ktorá patrí do nepokresleného intervalu začínajúceho pravou susedou jahody, na ktorej sme, a končiaceho prvou pokreslenou jahodou.) Napríklad v situácií na obrázku interval vpravo obsahuje jahody \(3\) a \(4\) a interval vľavo jahodu \(6\).

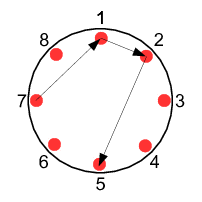
Nášmu programu by teda stačilo, keby si udržiaval dva intervaly, a pri každej novej jahode sa pozrel, či patrí do jedného z nich; ak áno, príslušne si intervaly upravil, a ak nie, vyhlásil by, že sa čiara pretne. Môžeme si ale všimnúť, že ak za začiatok pravého intervalu vyhlásime prvú pokreslenú jahodu, ktorá je napravo od naposledy navštívenej jahody a za koniec tú, ktorá je pravou susedou naposledy navštívenej jahody, a pre ľavý interval to spravíme naopak (začiatok na susede naposledy navštívenej jahody), tak interval, ktorý začína začiatkom pravého intervalu a končí koncom ľavého intervalu, obsahuje práve všetky jahody navštíviteľné v najbližšom kroku plus jahodu, na ktorej práve sme. Keďže zadanie nám zaručuje, že jahody sa v pláne nebudú opakovať, môžeme si prácu uľahčiť tým, že budeme kontrolovať príslušnosť nasledujúcej jahody len do jedného intervalu, a nie do dvoch. Na obrázku by to znamenalo, že začiatok spojeného intervalu bude na jahode \(2\) a koniec na jahode \(7\) (pričom interval “ide” v smere hodinových ručičiek).

Ako teda náš program funguje? Keď načítame prvú jahodu, nastavíme si začiatok (\(z\)) a koniec (\(k\)) intervalu a aktuálnu (\(a\)) aj poslednú (\(p\)) jahodu na tú, ktorú sme práve načítali. Pri načítaní každej ďalšej jahody (uložíme si ju do \(a\)) skontrolujeme, či \(a\) patrí do intervalu \([z, k]\) – to spravíme zistením, či je \(a\) vzdialená od \(z\) v smere hodinových ručičiek najviac o toľko, o koľko je v rovnakom smere vzdialené \(k\) (keďže \(k\) aj \(z\) sú už pokreslené, nemôže sa stať, že by \(a = z\) alebo \(a = k\)). Ak nie, zapamätáme si, že čiara sa pretne. Nakoniec si zaktualizujeme interval (čiže jeden z jeho koncov zmeníme na \(p\) – to, ktorý, určíme podľa toho, v ktorej jeho časti leží aktuálna jahoda) a nastavíme \(p = a\).

Na záver ešte pár slov o zložitosti. Keďže náš program používa len zopár premenných (ich počet nezávisí od veľkosti vstupu), jeho pamäťová zložitosť je konštantná – \(O(1)\). Pre každý vstup spraví v cykle, ktorého dĺžka závisí od veľkosti vstupu, konštantne veľa krokov, takže jeho časová zložitosť je lineárna od veľkosti vstupu – \(O(m)\). Všimnime si, že obe zložitosti sú optimálne – pamäť \(O(1)\) sa nedá vylepšiť zo zrejmých dôvodov, a čas \(O(m)\) sa nedá vylepšiť preto, lebo toľko trvá už samotné načítanie vstupu.

#include <cstdio>

int n, m;

bool je_v_intervale(int a, int z, int k) {
    return (a-z+n)%n <= (k-z+n-1)%n; //-1 je tam kvoli prvej jahode, vtedy k = z
}

void sprav() {
    scanf("%d%d", &n, &m);
    int z, k, p, a;
    bool pretne = false;
    for(int i = 0; i < m; ++i) {
        scanf("%d", &a);
        a--; //chceme pracovat s cislami od 0 po n-1, nie od 1 po n
        if (i==0) {
            z = k = p = a;
        } else {
            if (!je_v_intervale(a, z, k)) pretne = true;
            if (je_v_intervale(a, z, p)) k = p;
            else z = p;
            p = a;
        }
    }
    printf("%sPRETNE\n", pretne?"":"NE");
}

int main(){
    int T;
    scanf("%d", &T);
    while(T--) sprav();
}