Zadanie
Bubu sa jedného dňa prechádzal po lese, keď mu do oka padol šuter. Chvalabohu, iba metaforicky, nie doslova. Šutrák to bol riadny, čo Bubua potešilo, až radostne zýýkol (Yyyyyy!). No keď si Bubu uvedomil, že má tento balvan v ceste, radosť ho prešla. Pobral sa ho obísť, no hneď za šutrom, na čistine, mu jeden strom, starý hodne, zahatil, aby nezaspal, preventívne cestu tým, že sa vyvalil. Bubu sa nenechal odradiť a aj túto prekážku obišiel. Potom, čo obišiel tento strom, sa mu kdesi v podlesí zjavili v ceste dva vresy (a to riadne prerastené). Za mohutným sudom od kapusty (ktorý musel tiež chudák obchádzať) ležali vyvalené 4 bresty. A tak ďalej, (no viete si to domyslieť), no a keď bol koniec prechádzky, tak mu do cesty vošli sanitky.
Tak s potom až na brade, vo vysilenej nálade, Bubu dokončil svoje trápenie počnuté kusom žuly. Teraz hľadá optimálne riešenie ako obísť skaly.
Úloha
Vašou úlohou je nájsť najkratšiu trasu z pozície udanej začiatočnými koordinátmi na pozíciu udanú konečnými koordinátmi, ktorá neprechádza žiadnou z popísaných prekážok. Prekážky sú buď úsečkami, alebo konvexnými mnohouholníkami.
Vo všeobecnosti platí, že sa tieto prekážky nedotýkajú. Inak povedané, začiatok a koniec žiadnej úsečky, vrátane vrcholov mnohouholníkov, nikdy neležia uprostred inej úsečky. (V niektorých sadách sa ale úsečky môžu pretínať a zdieľať koniec/začiatok)
Pozn.: Cesta môže prechádzať pozdĺž prekážky, aj cez jej začiatok a koniec, ale nie cez samotnú prekážku, čo v prípade mnohouholníkov znamená, že môže ísť po obvode ale nie cez ich vnútro.
Formát vstupu
Na prvom riadku vstupu sú štyri čísla \(x_s,\) \(y_s,\) \(x_e,\) \(y_e\) popisujúce koordináty začiatku (\(x_s,\) \(y_s\)) a konca (\(x_e,\) \(y_e\)) trasy, ktorú chce Bubu prejsť.
Druhý riadok obsahuje jedno číslo \(n\), počet prekážok.
Nasleduje \(2n\) riadkov, ktoré po pároch popisujú prekážky na trase. Riadok číslo \(2k\) obsahuje jedno číslo \(m_k\geq 2\), počet bodov popisujúcich \(k\)-tú prekážku. V prípade, že \(m_k=2\), je prekážka úsečkou, v opačnom prípade je mnohouholníkom.
Riadok číslo \(2k+1\) obsahuje \(2m_k\) čísel vo formáte \(x_0,\) \(y_0,\) \(\dots\) \(x_{m_k-1},\) \(y_{m_k-1}\), ktoré popisujú koordináty prekážky, v poradí.
V jednotlivých sadách platia nasledujúce obmedzenia:
| Sada | 1, 2 | 3, 4 | 5, 6 | 7, 8 |
|---|---|---|---|---|
| \(1 \leq \sum m_i \leq\) | \(20\) | \(60\) | \(150\) | \(200\) |
V sadách 1, 2, 3, 4 môžete predpokladať, že sa žiadne dve úsečky nepretínajú. V sadách 1, 3, 5, 7 navyše platí \(m_i=2\), vo všeobecnosti platí \(m_i\leq10\).
Formát výstupu
Vypíšte dĺžku najkratšej možnej trasy zo začiatku na koniec. Váš výsledok by mal byť najviac \(10^{-6}\) rozdielny od očakávaného výsledku.
Príklady
Input:
0.0 0.0 4.0 0.0
3
2
1.0 -1.0 1.0 1.0
2
2.0 4.0 2.0 0.0
2
3.0 1.0 3.0 -4.0Output:
5.656854249492381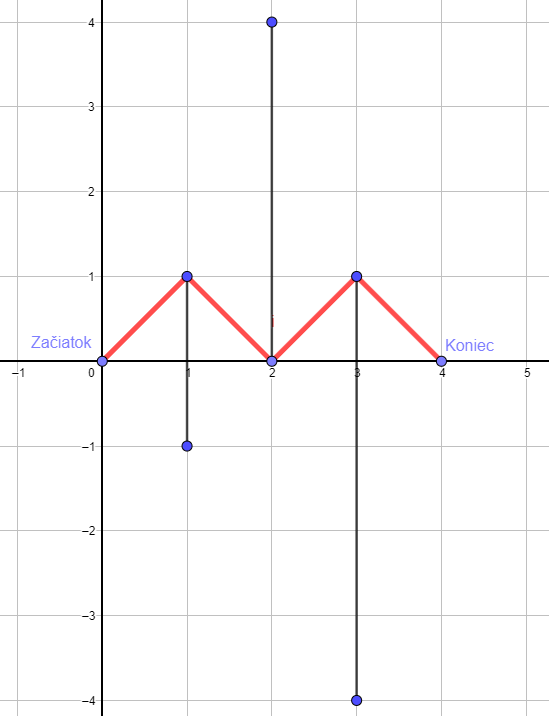
Prekážky sú čierne úsečky s vyznačeným koncom a začiatkom, optimálna trasa je červenou.
Input:
0.0 0.0 4.0 0.0
4
2
1.0 -1.0 1.0 1.0
2
2.0 4.0 2.0 0.0
2
2.0 0.0 2.0 -4.0
2
3.0 1.0 3.0 -1.0Output:
5.656854249492381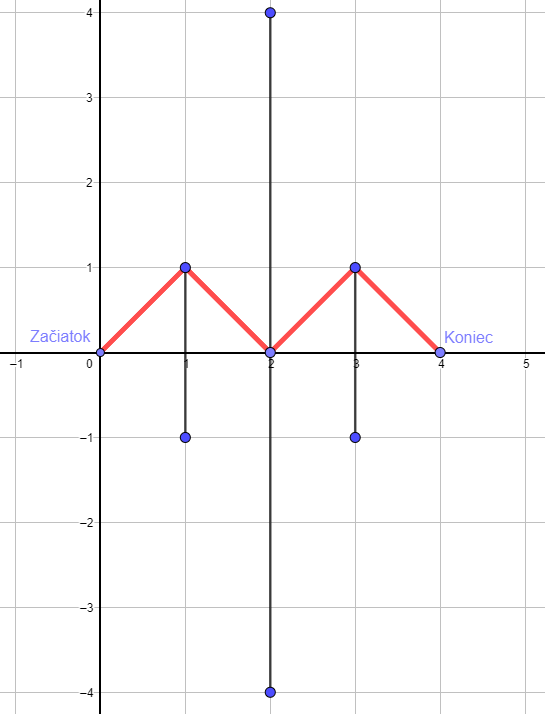
V prípade, že dve úsečky zdieľajú jeden koniec, môže tade prechádzať trasa.
Input:
0.0 0.0 6.0 0.0
1
4
2.0 2.0 2.0 -2.0 4.0 -2.0 4.0 2.0Output:
7.656854249492381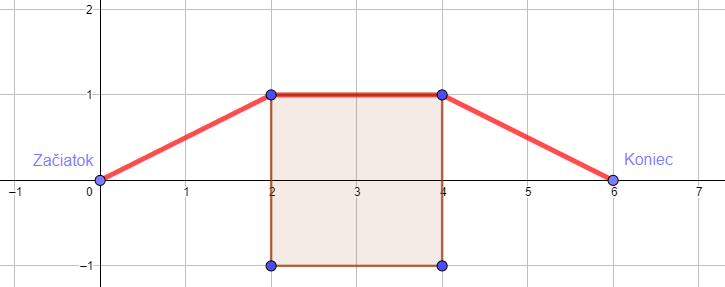
Podobne ako vyššie, štvorcová prekážka je hnedou.
Kľúčom k riešeniu tejto úlohy je uvedomiť si dve veci. Za prvé: najkratšia trasa medzi dvomi bodmi je úsečka. Za druhé: smer, ktorým ideme sa nám neoplatí meniť nikde inde, ako na bodoch, ktoré definujú prekážky (konce v prípade úsečiek a rohy v prípade n-uholníkov).
Vďaka týmto dvom poznatkom vieme použiť abstrakciu, ktorou si celý problém vieme zjednodušiť na graf, v ktorom potom už len stačí nájsť najkratšiu trasu. Vrcholmi tohoto grafu budú štart, koniec, a body, ktoré definujú prekážky. Hrany v tomto grafe budú existovať iba v prípade, že medzi danými dvoma vrcholmi existuje priama úsečka, ktorá neprechádza žiadnou prekážkou. Keďže hľadáme najkratšiu cestu v 2D priestore, musíme každej hrane priradiť aj jej dĺžku, ktorá bude rovnaká, ako dĺžka príslušnej úsečky.
(Táto abstrakcia funguje iba v prípade, že sa žiadne úsečky nedotýkajú, čo je špecifikované v zadaní)
Keďže má náš graf hrany s definovanou dĺžkou, jednoduché BFS nám nebude stačiť na nájdenie najkratšej trasy. Na to musíme použiť Dijkstrov algoritmus, ktorý túto trasu ľahko nájde.
Ku kompletnému teoretickému riešeniu nám teda chýba jediná vec, a to síce, ako si tento graf vyrobiť.
Generácia grafu
Ak chceme vygenerovať náš graf, musíme vedieť, ktoré hrany v ňom sú, a ktoré nie. Vec sa má tak, že teoreticky v ňom môže byť každá možná hrana medzi dvoma vrcholmi a bez toho, aby sme ich všetky skontrolovali nemôžeme žiadnu vylúčiť (až na výnimky, ktoré spomeniem nižšie). Náš prístup teda skontroluje každú dvojicu vrcholov, a zistí, či úsečka medzi nimi neprechádza cez žiadnu prekážku. Ak nie, môžeme ju pridať do grafu. Jej dĺžku ľahko vyrátame pomocou Pytagorovej vety.
V prípade, že všetky prekážky sú úsečkami (nepárne sady) je to celkom jednoduché: pre každú potenciálnu hranu skontrolujeme všetky prekážky, a ak ju niektorá pretína, vieme, že táto hrana nie je v grafe.
V prípade n-uholníkov je to trochu komplikovanejšie. Nemôžeme ich priamo zjednodušiť na úsečky, keďže ich vnútro je tiež nepriechodné. Iba, že by sme použili nejaký trik. Obvod n-uholníkov teda zjednodušíme na úsečky. Možností, ako vyriešiť vnútro je veľa.
Našim prístupom je, že vôbec nebudeme generovať hrany pre body, ktoré sa nachádzajú vnútri n-uholníkov (týmto automaticky vylúčime akékoľvek hrany, ktoré vchádzajú do a vychádzajú z n-uholníkov). Diagonály medzi rôznymi bodmi toho istého n-uholníka vieme veľmi ľahko skontrolovať a zakázať, keďže poznáme poradie bodov v n-uholníku.
Jediný problém, ktorý nám zostáva, sú hrany, ktoré prechádzajú krížom cez n-uholník, tak, že na nich ležia dva rohy n-uholníka. To vieme vyriešiť tak, že pri kontrole pretínania úsečiek vylúčime nielen prípad, kedy sa úsečky úplne pretnú, ale aj prípad, kedy sa dotknú. Zvyšok riešenia to neovplyvní, keďže v prípadoch, kde takéto úsečky potrebujeme nahradíme jednu úsečku \(AC\) dvoma (alebo viacerými) úsečkami \(AB\) a \(BC\), v súčte rovnakej dĺžky. No v prípade hrany, ktorá ide krížom cez n-uholník, by táto hrana bola rozdelená na tri hrany - dve, ktoré končia v rohoch n-uholníka a jedna diagonála. Túto diagonálu však už vylúčime, a teda je problém vyriešený.
Riešenie a zložitosti
Naše riešenie načíta vstup, vygeneruje podľa popisu vyššie graf, a následne na ňom spustí Dijkstrov algoritmus.
Časová zložitosť nášho riešenia je \(O(n^3)\), kde \(n\) je počet bodov definujúcich prekážky (\(n = \sum m_i\) ak použijeme značenie zo zadania), keďže pri generácii grafu kontrolujeme každú potenciálnu hranu (ktorých je \(O(n^2)\)) na pretnutie s každou úsečkou definujúcou prekážku (ktorých je \(O(n)\)). Dijkstrov algoritmus vieme implementovať s časovou zložitosťou \(O(n^2)\), čo celkovú časovú zložitosť neovplyvňuje.
Pamäťová zložitosť nášho riešenia je \(O(n^2)\), keďže najväčšia vec, ktorú si musíme pamätať je graf, kde si musíme pre každú hranu uložiť jej dĺžku, prípadne existenciu (keďže dĺžku môžeme vždy znovu vyrátať v konštantnom čase).
Vzorové riešenie
Asymptotickú časovú zložitosť tohoto riešenia síce nezlepšíme, no vieme zlepšiť jeho pamäťovú zložitosť, a praktickú časovú zložitosť. To vieme spraviť tak, že namiesto generácie grafu pred spustením Dijkstrovho algoritmu budeme kontrolovať existenciu hrany v grafe počas jeho behu. Na kontrolu existencie hrán použijeme rovnaký systém, ako sme použili na generáciu grafu, akurát ich budeme kontrolovať len keď ich treba.
Takéto riešenie má stále v najhoršom prípade časovú zložitosť \(O(n^3)\), keďže v každom kroku Dijkstrovho algoritmu musíme skontrolovať pre \(n\) potenciálnych ďalších bodov \(n\) potenciálnych prekážok na pretnutie (ak nerátame body, ktoré sme už použili tak v jednotlivých krokoch musíme v najhoršom prípade spraviť najviac \(n^2, n(n-1),\cdots, 2n, n\) kontrol, čo sa sčíta na \(O(n^3)\)). Prakticky však bude náš program na vstupoch bežať násobne rýchlejšie.
Pamäťová zložitosť tohoto riešenia je \(O(n)\), keďže si pamätáme len vstup a vzdialenosť každého bodu od začiatku, obe o veľkosti \(O(n)\).
Podobným prístupom vieme dospieť aj k ďalšej optimalizácii. K rozhodnutiu negenerovať celý graf nás síce viedlo zlepšenie pamäťovej zložitosti, avšak tento prístup nám dovolí obmedziť vykonávanie časovo veľmi náročnej operácie (kontrola existencie hrany medzi dvoma vrcholmi) iba na užitočné prípady, teda iba na tie dvojice vrcholov, ktoré reálne zvažujeme pri prehľadávaní. Pokračovaním tejto myšlienky vieme dospieť k optimalizácii, kedy existenciu hrany nekontrolujeme pri pridávaní, ale pri vyberaní kandidáta nasledujúceho vrcholu pri prehľadávaní. Vykonávame Dijkstrovo prehľadávanie a tvárime sa, že každá hrana existuje až do posledného možného momentu. Takýmto spôsobom minimalizujeme počet overovovaní existencie hrany, čo urýchli beh algoritmu. Ďalším praktickým vylepšením vie byť implementovanie prehľadávania A* namiesto Dijsktrovho algoritmu, čo je na grafoch na 2D ploche ľahký spôsob ako zrýchliť beh programu. Obe tieto optimalizácie stále nezlepšujú asymptotickú časovú zložitosť a nie sú potrebné na získanie plného počtu bodov za program. Prakticky však každé z nich zrýchľujú beh programu na naších vstupoch dvojnásobne.
#include <bits/stdc++.h>
using namespace std;
using ll = int;
using ld = long double;
#define len(x) ((ll)(x).size())
const ld INF = 1e100;
using point = complex<ld>;
using poly_t = vector<point>;
using edge_t = pair<ld, ll>;
using graph_t = vector<vector<edge_t>>;
using polypoints_t = vector<tuple<point, ll, ll>>;
inline ll previ(ll i, ll n) { return i - 1 + n * (i <= 0); }
inline ll nexti(ll i, ll n) { return i + 1 - n * (i >= n - 1); }
inline ld cross(point a, point b) { return (conj(a) * b).imag(); }
inline ld orient(point a, point b, point c) { return cross(b - a, c - a); }
inline bool inside_polygon(poly_t &poly, point p) {
if (len(poly) < 3) return false;
ld dir = orient(poly[0], poly[1], p);
for (ll b = 0; b < len(poly); ++b)
if (dir * orient(poly[previ(b, len(poly))], poly[b], p) <= 0)
return false;
return true;
}
inline bool lines_intersect(point a1, point a2, point b1, point b2) {
return abs(cross(a2 - a1, b2 - b1)) > 1e-10 &&
orient(b1, b2, a1) * orient(b1, b2, a2) <= 0 &&
orient(a1, a2, b1) * orient(a1, a2, b2) <= 0 &&
(a1 != b1 && a1 != b2 && a2 != b1 && a2 != b2);
}
inline bool line_intersects_polygon(point a1, point a2, poly_t &poly) {
if (len(poly) < 2) return false;
for (ll b = 0; b < len(poly); ++b)
if (lines_intersect(a1, a2, poly[previ(b, len(poly))], poly[b]))
return true;
return false;
}
inline graph_t get_graph(vector<poly_t> &polys) {
ll pn = accumulate(polys.begin(), polys.end(), 0,
[](size_t a, const auto &c) { return a + len(c); }
);
vector<bool> inside;
inside.reserve(pn);
for (auto &poly: polys)
for (auto pt: poly)
inside.push_back(any_of(polys.begin(), polys.end(), [&](auto &pl) {
return inside_polygon(pl, pt);
}));
graph_t res(pn);
auto consider_edge = [&](ll v1, point p1, ll v2, point p2) {
if (inside[v1] || inside[v2] ||
any_of(polys.begin(), polys.end(), [&](auto pl) {
return line_intersects_polygon(p1, p2, pl);
}))
return;
ld dist = abs(p1 - p2);
res[v1].push_back({dist, v2});
res[v2].push_back({dist, v1});
};
ll v1 = 0;
for (ll polyi1 = 0; polyi1 < len(polys); ++polyi1) {
auto &poly1 = polys[polyi1];
for (ll pi1 = 0; pi1 < len(poly1); ++pi1, ++v1) {
if (inside[v1]) continue;
point p1 = poly1[pi1];
if (len(poly1) >= 2) {
ll pi2 = previ(pi1, len(poly1));
ll v2 = v1 - pi1 + pi2;
consider_edge(v1, p1, v2, poly1[pi2]);
}
ll v2 = 0;
for (ll polyi2 = 0; polyi2 < polyi1; ++polyi2) {
auto &poly2 = polys[polyi2];
for (ll pi2 = 0; pi2 < len(poly2); ++pi2, ++v2)
consider_edge(v1, p1, v2, poly2[pi2]);
}
}
}
return res;
}
inline point read_point() {
ld x, y;
cin >> x >> y;
return point(x, y);
}
inline vector<poly_t> parse_input() {
point pS = read_point();
point pF = read_point();
ll polyN;
cin >> polyN;
vector<poly_t> polys(2 + polyN);
polys[0] = {pS};
polys[1] = {pF};
for (ll pli = 2; pli < len(polys); ++pli) {
ll pn;
cin >> pn;
polys[pli].resize(pn);
for (auto &p: polys[pli])
p = read_point();
}
return polys;
}
inline polypoints_t get_polypoints(vector<poly_t> &polys) {
polypoints_t points = {};
for (ll pli = 0; pli < len(polys); ++pli)
for (ll pti = 0; pti < len(polys[pli]); ++pti)
points.push_back({polys[pli][pti], pli, pti});
return points;
}
ld solve(vector<poly_t> &polys, polypoints_t &points) {
ll pn = len(points);
vector<bool> inside(pn);
for (ll i = 0; i < pn; ++i)
inside[i] = any_of(polys.begin(), polys.end(), [&](auto &pl) {
return inside_polygon(pl, get<0>(points[i]));
});
auto consider_edge = [&](ll v1, point p1, ll v2, point p2) {
return !(inside[v1] || inside[v2] ||
any_of(polys.begin(), polys.end(), [&](auto pl) {
return line_intersects_polygon(p1, p2, pl);
}));
};
vector<bool> seen(pn, false);
vector<ld> res(pn, INF);
res[0] = 0;
set<edge_t> PQ;
PQ.insert({0, 0});
while (!PQ.empty()) {
auto [dist, pi1] = *PQ.begin();
PQ.erase(PQ.begin());
if (pi1 == 1) break;
seen[pi1] = true;
point p1; ll pli1, pl_pti1;
tie(p1, pli1, pl_pti1) = points[pi1];
ll len_poly1 = len(polys[pli1]);
ll prev_pt2 = previ(pl_pti1, len_poly1);
ll next_pt2 = nexti(pl_pti1, len_poly1);
for (ll pi2 = 0; pi2 < pn; ++pi2) {
if (seen[pi2])
continue;
auto [p2, pli2, pl_pti2] = points[pi2];
ld dist2 = dist + abs(p1 - p2);
if (res[pi2] <= dist2 ||
(pli1 == pli2 && pl_pti2 != prev_pt2 && pl_pti2 != next_pt2) ||
!consider_edge(pi1, p1, pi2, p2)
)
continue;
PQ.erase({res[pi2], pi2});
res[pi2] = dist2;
PQ.insert({res[pi2], pi2});
}
}
return res[1];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
auto polys = parse_input();
auto points = get_polypoints(polys);
ld res = solve(polys, points);
cout << setprecision(18) << fixed << res << '\n';
}import heapq
point = complex
poly_t = list[point]
graph_t = list[list[tuple[float, int]]]
polypoints_t = list[tuple[point, int, int]]
INF = 1e100
def cross(a: point, b: point) -> float:
return (a.conjugate() * b).imag
def orient(a: point, b: point, c: point) -> float:
return cross(b - a, c - a)
def inside_polygon(poly: poly_t, p: point) -> bool:
if len(poly) < 3: return False
dir = orient(poly[0], poly[1], p)
return not any(dir * orient(poly[b - 1], poly[b], p) <= 0 for b in range(len(poly)))
# tu ignorujeme pripad kedy su usecky paralelne a zdielaju cast dlzky
def lines_intersect(a1: point, a2: point, b1: point, b2: point) -> bool:
return (
abs(cross(a2 - a1, b2 - b1)) > 1e-10 and
orient(b1, b2, a1) * orient(b1, b2, a2) <= 0 and
orient(a1, a2, b1) * orient(a1, a2, b2) <= 0 and
(a1 != b1 and a1 != b2 and a2 != b1 and a2 != b2)
)
def line_intersects_polygon(a1: point, a2: point, poly: poly_t) -> bool:
return len(poly) >= 2 and \
any(lines_intersect(a1, a2, poly[b - 1], poly[b]) for b in range(len(poly)))
def parse_input() -> list[poly_t]:
l = tuple(map(float, input().split()))
point_start, point_finish = point(*l[:2]), point(*l[2:])
polyN = int(input())
polys: list[poly_t] = [[point_start], [point_finish]] + [[] for _ in range(polyN)]
for poly_idx in range(2, 2 + polyN):
_ = int(input())
l = tuple(map(float, input().split()))
polys[poly_idx] = [point(l[i], l[i+1]) for i in range(0, len(l), 2)]
return polys
def get_polypoints(polys: list[poly_t]) -> polypoints_t:
points: polypoints_t = []
for poly_idx in range(len(polys)):
for pt_i, p in enumerate(polys[poly_idx]):
points.append((p, poly_idx, pt_i))
return points
def solve(polys: list[poly_t], points: polypoints_t) -> float:
n_points = len(points)
inside = [any(inside_polygon(pl, pt) for pl in polys) for poly in polys for pt in poly]
def consider_edge(v1: int, p1: point, v2: int, p2: point) -> float:
return not (inside[v1] or inside[v2] or # trasa nemoze prechadzat bodom v strede n-uholnika
any(line_intersects_polygon(p1, p2, pl) for pl in polys) # ani krizom cez prekazky
)
res = [INF] * n_points
point_queue: list[tuple[float, int, int]] = [(0.0, 0, 0)]
while point_queue:
dist, pt_i_1, pt_i_0 = heapq.heappop(point_queue)
if res[pt_i_1] < INF or not consider_edge(pt_i_0, points[pt_i_0][0], pt_i_1, points[pt_i_1][0]):
continue
res[pt_i_1] = dist
if pt_i_1 == 1:
break
p1, pli1, pl_pti1 = points[pt_i_1]
len_poly1 = len(polys[pli1])
prev_pt2 = (pl_pti1 if pl_pti1 else len_poly1) - 1
next_pt2 = (pl_pti1 if pl_pti1 != len_poly1 - 1 else -1) + 1
for pt_i_2 in range(n_points):
if res[pt_i_2] < INF:
continue
p2, pli2, pl_pti2 = points[pt_i_2]
if pli1 == pli2 and pl_pti2 != prev_pt2 and pl_pti2 != next_pt2:
continue # trasa medzi bodmi rovnakeho n-uholnika moze ist len po obvode
heapq.heappush(point_queue, (dist + abs(p1 - p2), pt_i_2, pt_i_1))
return res[1]
if __name__ == '__main__':
polys = parse_input()
points = get_polypoints(polys)
res = solve(polys, points)
print(f"{res:.18f}")Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.