Zadanie
“Let’s make some happy little trees,” povedal Bob Ross1 a začal kresliť stromy na plátno. Inšpirovaná týmto známym umelcom, zobrala Paulínka svoje obľúbené voskovky a začala kresliť stromy na papier.
Paulínka rada kreslí zakorenené informatické stromy, a aby bol výsledný obrázok čo najkrajší, musia byť všetky stromy rôzne a zároveň musia všetky pochádzať z rovnakého materského stromu. (Potom môže obdivovateľom umenia hovoriť, že stromy majú spoločnú dušu.) V časti úloha hneď vysvetlíme, čo to znamená.
Pomôžte Paulínke zistiť, koľko najviac stromov, môže nakresliť, aby splnila želané podmienky. A nezabudnite, keby sa vám to aj na prvý pokus nepodarilo, Bob Ross má pre vás jednu múdrosť: “We don’t make mistakes, we have happy accidents.”
Úloha
Informatický strom (ďalej len strom) je množina \(n\) vrcholov a \(n-1\) hrán, taká, že z každého vrcholu do každého vedie práve jedna cesta. Zakorenený informatický strom (ďalej len zakorenený strom) je strom, v ktorom sme jeden vrchol vybrali ako koreň.
Zo stromu vieme vytvoriť \(n\) zakorenených stromov tak, že postupne označíme každý z \(n\) vrcholov ako koreň (viď obrázok pri prvom príklade vstupu).
Pre tieto zakorenené stromy si zavedieme nový pojem, rovnakosť, ku ktorému opačný pojem je rôznosť. Zakorenené stromy budeme volať rovnaké, keď sa líšia len v označení vrcholov a v poradí synov každého vrcholu. T.j. pokiaľ dovolíme ľubovoľne prehadzovať poradie synov, vieme pretvoriť jeden strom na druhý. Pokiaľ sa takto nedajú pretvoriť, tak uvažujeme, že sú stromy rôzne.
Formálna definícia by mohla byť nasledovná: Dva zakorenené stromy voláme rovnaké, ak existuje bijektívne zobrazenie2 \(f\) vrcholov jedného stromu na vrcholy druhého stromu, také že pre všetky \(x,y\) platí, že \(x\) je otec \(y\) práve vtedy, keď \(f(x)\) je otec \(f(y)\).
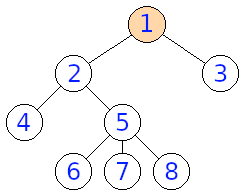
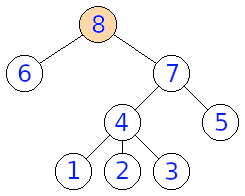
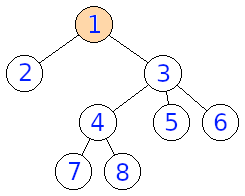
Na obrázkoch môžeme vidieť príklady troch stromov, z ktorých prvé dva sú rovnaké a tretí je od oboch rôzny. Zobrazenie, ktoré spĺňa formálnu definíciu je \(1,2,3,4,5,6,7,8 \rightarrow 8,7,6,5,4,1,2,3\), ale aj \(1,2,3,4,5,6,7,8 \rightarrow 8,7,6,5,4,3,2,1\)
Na vstupe máte zadaný strom. Vypíšte koľko najviac navzájom rôznych zakorenených stromov môžeme dostať označením niektorého vrcholu tohto stromu ako koreň.
Formát vstupu
Na prvom riadku vstupu sa nachádza číslo \(n\) – počet vrcholov zadaného stromu. Vrcholy sú očíslované \(1\) až \(n\).
Na nasledujúcich \(n-1\) riadkoch su vymenované hrany zadaného stromu, na každom riadku sú čísla dvoch vrcholov, \(a_i, b_i\), ktoré táto hrana spája. \(1\leq a_i, b_i \leq n\)
Formát výstupu
Na výstup vypíšte jedno číslo – počet rôznych zakorenených stromov, ktoré dostaneme, ak postupne každý z vrcholov označíme ako koreň.
Hodnotenie
Je 8 sád vstupov. Platia v nich nasledovné obmedzenia:
| Sada | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \(2 \leq n \leq\) | \(10\) | \(100\) | \(100\) | \(1\,000\) | \(1\,000\) | \(50\,000\) | \(100\,000\) | \(300\,000\) |
Príklady
Input:
4
1 2
2 3
3 4Output:
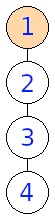
2Ak strom zakoreníme za prvý alebo posledný vrchol, dostaneme rovnaký strom. Podobne dostaneme rovnaké stromy, ak ho zakoreníme za druhý alebo tretí. Vieme teda nakresliť dva rôzne zakorenené stromy.
Na obrázku nižšie môžeme vidieť, aké stromy dostaneme, pokiaľ zakoreníme vstupný strom postupne vo vrcholoch \(1, 2, 3, 4\)
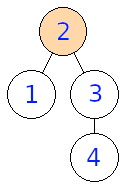
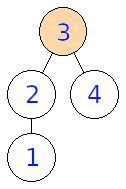
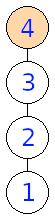
Input:
11
1 2
2 3
3 4
4 5
4 6
4 7
5 10
10 9
10 8
7 11Output:
10Input:
7
7 1
7 2
3 2
7 4
5 4
6 5Output:
7Príklad Bobovej tvorby nájdete na youtu.be/0n4f-VDjOBE.↩︎
každému vrcholu prvého stromu je priradený práve jeden vrchol z druhého stromu↩︎
To, čo sme v zadaní volali rovnakosť sa v informatike zvykne nazývať izomorfizmus. Ďalej teda budeme hovoriť, že dva zakorenené stromy sú izomorfné, ak existuje bijektívne zobrazenie \(f\) vrcholov jedného stromu na vrcholy druhého stromu, také že pre všetky \(x,y\) platí, že \(x\) je otec \(y\) práve vtedy, keď \(f(x)\) je otec \(f(y)\). (Toto je rovnaká definícia ako v zadaní, len na pripomenutie.)
Intuitívna predstava izomorfizmu je, že zodpovedajúce vrcholy sa môžu líšiť len v poradí synov. Toto je dôležité mať na pamäti.
Mimochodom, keď máme zakorenený strom za koreň \(v\), tak stromy, ktorých korene sú synovia \(v\), budeme volať podstromy tohto stromu, alebo podstromy koreňa, alebo podobne. Občas budeme zamieňať pojmy podstrom a vrchol, väčšinou by malo byť jasné, že ide o tú istú vec. Ak napríklad označíme vrchol \(u\) nejakým číslom, tak toto číslo obvykle hovorí niečo o celom podstrome.
Obsah
Riešenie si rozdelíme na niekoľko častí:
V prvej časti sa pozrieme na to, ako algoritmicky spočítať, či ľubovoľné dva stromy sú izomorfné. Ukážeme si tri spôsoby, jeden z nich ilustruje podstatu zvyšných dvoch spôsobov, avšak je pomalý. Zvyšné dva implementujú túto podstatu efektívne, či už pomocou hashovania alebo pomocou iných techník. Obe rýchlejšie riešenia budú vedieť porovnať dva stromy v čase \(O(n)\), hoci v jednom prípade si podrobne rozoberieme iba jednoduchšiu \(O(n \log n)\) variantu.
V druhej časti sa pozrieme, ako zovšeobecniť algoritmus z dvoch stromov na izomorfizmus \(n\) stromov, a následne ako pomocou toho vyriešiť samotnú úlohu v celkovom čase \(O(n)\) resp. \(O(n\log n)\).
Na plný počet bodov za popis úlohy stačí časová zložitosť \(O(n\log n)\) a zároveň žiaden riešiteľ neodovzdal popis deterministického riešenia so zložitosťou \(O(n)\), takže nebudú ani bonusové body ;)
Izomorfizmus dvoch stromov – naivné riešenie
Stromy porovnávať zatiaľ nevieme, ale napríklad také reťazce znakov vieme porovnávať celkom dobre. Čo keby sme každý strom zapísali ako reťazec znakov? Celkom štandardný zápis zakoreného stromu je: ľavá zátvorka, zreťazené zápisy všetkých podstromov koreňa, pravá zátvorka.
Napríklad jednovrcholový strom, má zápis “()”, trojvrcholový binárny strom má zápis “(()())”, reťaz vysoká 3 má zápis “((()))”. Na obrázku môžete vidieť pri každom vrchole zápis zodpovedajúceho podstromu.
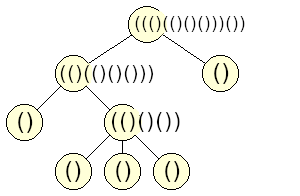
Žiaľbohu a niekedy aj chvalabohu, izomorfné stromy môžu mať rôzny zápis, lebo v tomto zápise záleží na poradí podstromov. Tento problém však ľahko vyriešime, nasledovnou zmenou. Nový zápis zakoreneného stromu bude: ľavá zátvorka, zretazené abecedne zoradené zápisy všetkých podstromov koreňa, pravá zátvorka.
Dôkaz, že s touto definíciou, dva stromy majú rovnaký zápis práve vtedy, keď sú izomorfné, necháme ako cvičenie pre čitateľa. Na obrázku môžeme vidieť príklad pre dva izomorfné stromy.
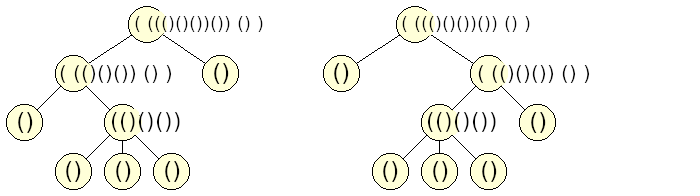
Skonštruovať zápis celého stromu nám môže v najhoršom prípade (dlhá reťaz) trvať až \(O(n^2)\). Porovnať dva zápisy a tým overiť izomorfizmus stromov potom vieme už v lineárnom čase.
Izomorfizmus dvoch stromov – hashovanie
Celý problém predošlého algoritmu je, že zápis stromu je potenciálne veľmi dlhý reťazec. Čo keby sme dokázali celý strom zapísať ako jedno číslo? Na základe predošlej úvahy by toto číslo malo byť rekurzívne definované cez podstromy a zároveň nezávislé od poradia podstromov.
Ako riešenie sa nám ponúka nasledovná hashovacia funkcia. Hash stromu \(T\) bude \[H_T = chaos(S \mod M) = chaos\left(\left(\sum_{t\in P(T)} H_t\right) \mod M\right)\]
kde \(P(T)\) je zoznam podstromov stromu \(T\), resp. \(S\) je súčet hashov podstromov stromu \(T\). \(M\) je nejaké prvočíslo, ktorým modulujeme, aby nám udržala rozumná veľkosť čísel. \(chaos\) je funkcia, ktorá pre každý vstup z \(\{0..M\}\) vráti iný náhodný výstup z \(\{0..M\}\).
Čo prosím? (Sa právom pýtate). V prvom rade súčet hashov podstromov je jednoduchý spôsob, ako zabezpečiť, aby nezáležalo na poradí podstromov. Potom ale potrebujeme, aby sa hashovacia funkcia nesprávala lineárne (t.j. zväčšenie nejakého zo vstupov o \(x\) zväčší výstup o \(kx\)), lebo to by sa nám ľahko stalo, že presun jedného vrchola z jedného podstromu do iného by nemuselo zmeniť hash (na jednom mieste \(+kx\), na inom \(-kx\), výsledok rovnaký), hoci by zmenilo izomorfizmus. A čo sa správa menej lineárne ako random?
Funkciu chaos môžeme implementovať lazy spôsobom – keď nám príde nový vstup, aký sme ešte nevideli, vygenerujeme si nový náhodný výstup a zapamätáme si ho. Ak nám príde vstup, aký už sme niekedy videli, vrátime zapamätanú hodnotu. Buď si môžeme dávať explicitne pozor, aby sme vždy vygenerovali iný výstup, alebo pokiaľ \(M >> n^2\), je pomerne malá šanca, že by nastala kolízia.
S touto hashovacou funkciou, dva izomorfné stromy majú vždy rovnaký hash, a dva neizomorfné stromy majú s veľkou pravdepodobnosťou rôzny hash. Stále môže nastať neželaná kolízia, ale tak to pri hashovacích algoritmoch často býva a tak v princípe iba nastavíme dostatočne veľké \(M\) a dúfame, že to bude fungovať.
Spočítať hash celého podstromu dokážeme rekurzívne v čase \(O(n)\)
Izomorfizmus dvoch stromov – labely a AHU
Ak sa nechceme spoliehať na náhodu, môžeme skúsiť nájsť iný spôsob, ako každému stromu priradiť jedno číslo, nazvime ho label (čítaj lejbl).
Pre spočítanie labelu stromu najprv rekurzívne spočítame labely všetkých podstromov, a zoberieme utriedený zoznam týchto labelov. Napríklad, pre list stromu (ktorý nemá žiadnych potomkov) dostaneme prázdny zoznam []. Ak má koreň stromu 5 synov s labelami 2,11,4,2,4, dostaneme zoznam [2,2,4,4,11].
Vždy, keď dostaneme takto utriedený zoznam, buď vidíme takýto zoznam prvýkrát a pridelíme mu najmenšie nepoužité prirodzené číslo ako label, alebo sme už zoznam videli a tak použijeme rovnaký label ako naposledy. Tu je príklad ako by vyzerali labely pre ukážkový strom a jeho podstromy. (Labely číslujeme od nuly).
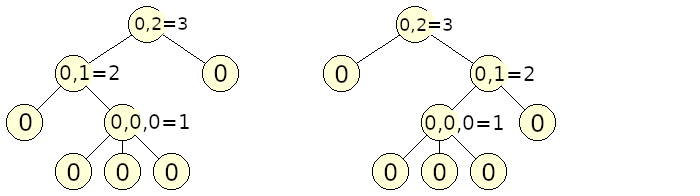
Ako vieme efektívne priraďovať, labely zoznamom? Napríklad pomocou mapy (vyvažovaný binárny strom), kde zoznam bude kľúč a label bude hodnota. Na utriedenie zoznamu labelov podstromov a tiež vyhľadanie zoznamu v mape potrebujeme čas \(O(p \log p)\), kde \(p\) je dĺžka zoznamu, resp. počet potomkov vrchola. Keďže súčet počtu potomkov pre všetky vrcholy stromu je \(n-1\), celkový čas je \(O(n \log n)\).
Veľmi podobne funguje AHU algoritmus (Aho, Hopcroft and Ullman), čo je štandardný a asi najznámejší algoritmus na overenie izomorfizmu dvoch stromov. Tento algoritmus používa fakt, že dva stromy môžu byť izomorfné, iba ak majú rovnakú hĺbku (môžete si nechať chvíľku na zamyslenie, prečo je to tak). Potom izomorfizmus overujeme iba pre stromy s rovnakou hĺbkou, nech je to \(h\). Najprv spočítame labely pre vrcholy v hĺbke \(h\), potom pre vrcholy v hĺbke \(h-1\), atď. až po koreň. Na jednej úrovni vždy najprv spočítame všetky zoznamy a potom im naraz priradíme labely postupne od nuly. V AHU algoritme, môžeme použiť v rôznych hĺbkach ten istý label.
Vďaka tomu, že labely počítame po vrstvách, môžeme naraz skonštruovať v čase \(O(p)\), kde \(p\) je počet vrcholov vo vrstve. Celý algoritmus potom beží v čase \(O(n)\). Detaily sú nad rámec tohto vzoráku ale aspoň stručné zhrnutie je, že lexikograficky triedime samotné utriedené sekvencie labelov pomocou zovšeobecného radix-sortu pre rôzne dĺžky sekvencií a potom priradíme nové labely podľa tohto poradia. Jednotlivé sekvencie nemusíme triediť, lebo ich už konštruujeme v utriedenom poradí, a to tak, že spracúvame synov vrcholov na vyššej vrstve od najmenších labelov po najväčšie.
Ak vás to zaujíma a viete po anglicky, celý algoritmus na overenie izomorfizmu dvoch stromov je popísaný v knižke The Design and Analysis of Computer Algorithms z roku 1974, strana 84-85, example 3.2.
Izomorfizmus \(n\) stromov.
Ak máme \(n\) zakorenených stromov a každý z nich má \(n\) vrcholov, môžeme pomocou predošlých algoritmov spočítať zápis, hash, alebo label každého z nich, a potom overiť, koľko rôznych zápisov, hashov, resp. labelov vidíme. Toto vieme spraviť v čase \(O(n^3)\) resp. \(O(n^2)\), pretože zápis, hash, resp. label každého so stromov vieme spočítať v čase \(O(n^2)\) resp. \(O(n)\).
Riešenie, založené na tomto princípe, pokiaľ ako základ algoritmu použijeme hashovanie by mohlo vyzerať takto:
import random
import sys
sys.setrecursionlimit(1000000)
random.seed(47)
MOD = 10 ** 9 + 7
n = int(input())
E = [[] for _ in range(n)]
for i in range(n - 1):
a, b = [int(x) - 1 for x in input().split()]
E[a].append(b)
E[b].append(a)
_chaos = {}
def chaos(x):
if x not in _chaos:
_chaos[x] = random.randint(1, MOD - 1)
return _chaos[x]
def dfs(v, parent):
s = 0
for e in E[v]:
if e != parent:
s += dfs(e, v)
return chaos(s % MOD)
print(len(set(dfs(i, -1) for i in range(n))))Posledné dve časti vzoráku sa budú zaoberať tým, ako to spraviť rýchlejšie.
Vzorové riešenie – hashovaie
Máme teda nezakorenený strom a chceme vedieť, aký hash by mali všetky jeho zakorenené verzie. Označme si hash vrcholu \(u\) v strome zakorenenom za vrchol \(v\) ako \(H_v(u)\). Označme si tiež súčet hashov potomkov vrchola \(u\) v strome zakorenenom za vrchol \(v\) ako \(S_v(u)\). Ak si ešte pamätáme definíciu našej hash funkcie, tak
\[H_v(u) = chaos(S_v(u))\]
Zakoreňme si náš strom najprv za vrchol 1 a spočítajme všetky hashe s týmto koreňom, čiže \(H_1(v)\) pre všetky \(v\).
Následne pre vyriešenie úlohy nám stačí vedieť \(H_v(v)\) pre všetky \(v\), a to vieme spočítať pomerne jednoducho. Vačsinu informácie potrebnú na spočítanie už máme. Pokiaľ \(u\) je predok \(v\) (v strome zakorenenom za vrchol 1) a \(w_1..w_k\) sú potomkovia vrchola \(u\) okrem \(v\), tak platí, že
\[H_1(w_i) = H_v(w_i)\]
pre všetky \(i\in {1..k}\). Je to kvôli tomu, že podstromy pod \(w_i\) neobsahujú ani vrchol \(v\) ani vrchol \(1\), a teda je ich podoba rovnaká pri zakorenení či už za \(v\) alebo za \(1\).
Zároveň z definície našej hash funkcie vieme, že:
\[H_1(u) = chaos(S_1(u)) = chaos\left(H_1(v) + \sum_{i=1}^k{H_1(w_i)}\right)\]
\[H_v(u) = chaos(S_v(u)) = chaos\left(\sum_{i=1}^k{H_1(w_i)}\right) = chaos(S_1(u) - H_1(v))\]
\[H_v(v) = chaos(S_1(v)+H_v(u)) = chaos\left(S_1(v)+chaos(S_1(u)-H_1(v))\right) \]
Na ľavej strane je to, čo chceme vedieť a na pravej sú informácie spočítané v strome zakorenenom za prvý vrchol. Implementácia sú dve po sebe spustené rekurzívne prehľadania stromu (dfs_1 a dfs_2). Časová zložitosť je \(O(n)\), pamäťová tiež \(O(n)\)
import random
import sys
sys.setrecursionlimit(1000000)
random.seed(47)
MOD = 10 ** 16 + 99 # if this prime doesn't work, pick a larger one
n = int(input())
E = [[] for _ in range(n)]
S1, S2 = [0 for _ in range(n)], [0 for _ in range(n)]
for i in range(n - 1):
a, b = [int(x) - 1 for x in input().split()]
E[a].append(b)
E[b].append(a)
_chaos = {}
def chaos(x):
if x not in _chaos:
_chaos[x] = random.randint(1, MOD - 1)
return _chaos[x]
def dfs_1(v, parent):
for e in E[v]:
if e != parent:
S1[v] += dfs_1(e, v)
S1[v] = S1[v] % MOD
return chaos(S1[v])
def dfs_2(v, parent):
if parent < 0:
S2[v] = S1[v] % MOD
else:
sp = (S2[parent] - chaos(S1[v])) % MOD
S2[v] = (chaos(sp) + S1[v]) % MOD
for e in E[v]:
if e != parent:
dfs_2(e, v)
dfs_1(0, -1)
dfs_2(0, -1)
print(len(set(S2)))Vzorové riešenie – labely a AHU
Našim cieľom je efektívne všetkým \(n\) zakoreneným stromom, a všetkým vrcholom (tieto zodpovedajú menším stromom pod vrcholmi) v nich priradiť labely (čísla) také, že dva stromy majú rovnaké číslo práve vtedy, keď sú izomorfné.
Podobne ako v predošlej časti, label vrcholu \(u\), pokiaľ je celý strom zakorenený za \(v\), budeme volať \(L_v(u)\).
Zdalo by sa, že takto musíme skonštruovať potenciálne \(n^2\) labelov, ale v skutočností môže existovať najviac \(3n\) rôznych labelov, resp. stromov. Jeden label má každý vrchol ak je koreňom a najviac jeden ďalší label za každého suseda (ak by daný sused bol otcom vrchola). Dokopy majú všetky vrcholy v strome \(2n-2\) susedov. Vôbec nás ale nezaujíma, aké labely by dostali nejaké úplne iné stromy, mimo týchto \(3n\) stromov, a to nám dá trocha slobody.
Vo vzorovom riešení s hashovaním, sme v podstate riešili problém, že na spočítanie labelu vrcholu \(v\) potrebujeme spočítať label vrcholu \(u\) a naopak, ale obišli sme to dvoma dfs prechodmi a odčítavaním hashov. Iný spôsob je skúsiť nájsť nejaký jedinečný vrchol \(v\) taký, že strom zakorenený vo \(v\), nie je izomorfný so žiadnym iným stromom. Takýmto jedinečným vrcholom je centrum stomu, ktoré si hneď vysvetlíme.
Priemer stromu je vzdialenosť najvzdialenejších vrcholov v strome, resp. dĺžka najdlhšej cesty v strome. Na chvíľu ignorujme stromy s priemerom nepárnej dĺžky, neskôr sa k nim vrátime. Ak je priemer stromu párny, tak existuje takzvané centrum, čo je stred najdlhšej cesty. Aj keď najdlhších ciest môže byť viac, centrum je vždy jednoznačné (zamyslite sa prečo). Označme si centrum nášho stromu \(c\).
Ak zakoreníme strom za centrum, dostaneme najplytšie možné zakorenenie a navyše strom zakorenený za vrchol \(v\) má hĺbku rovnú vzdialenosti \(v\) od \(c\) plus hĺbka pri zakorenení za \(c\). Z tohto vyplýva zaujímavá vec – ak majú byť dve zakorenenia stromu izomorfné, musia byť ich korene rovnako vzdialené od centra.
Druhá, dôležitejšia, vec je, že strom zakorenený za centrum nie je izomorfný so žiadnym iným stromom. \(L_c(c) \neq L_v(u)\) pre žiadne \((v, u) \neq (c, c)\). Pre \(v=u\) nesedí hĺbka a pre ostatné nesedí počet vrcholov. Dokonca, ak aj strom zakoreníme za hociaký vrchol, tak \(L_v(c) \neq L_v(u)\) pre \(c\neq u\). Opäť dôvod je jednoduchý – všetky ostatné stromy pod \(v\) musia mať inú hĺbku a teda nemôžu byť izomorfné.
S týmito pozorovaniami by sme mali vedieť zvoliť takú definíciu \(L_v(u)\), ktorá sa dá ľahko spočítať a zároveň dostatočne spĺňa izomorfickú podmienku (až na jednu výjnimku, viď nižšie).
Definujme si \(L_v(c) = -1\) pre všetky \(v\), inak povedané, dáme centru label, ktorý nepoužijeme nikde inde. Pre všetky ostatné stromy použijeme na definíciu labelu postup, ktorý poznáme zo sekcie Izomorfizmus dvoch stromov - labely a AHU.
\[L_v(u) = m(S_v(u))\]
kde \(S_v(u)\) je utriedený zoznam labelov synov \(w\) vrchola \(u\) za predpokladu, že \(v\) je koreň. \(m\) je funkcia, ktorá na vstupe dostane zoznam celých čísel a na výstupe vráti jedno prirodzené číslo. Funkcia \(m\) vracia rovnaké čísla pre rovnaké zoznamy, a rôzne čísla pre rôzne zoznamy (inak povedané \(m\) je prostá funkcia). Implementácia takéhoto niečoho je jednoduchá pomocou mapy alebo hash-mapy (python vie dobre hashovať tuples).
Výstupom algoritmu je počet rôznych hodnôt \(L_v(v)\), ktoré spočítame podobne ako v predošlej sekcii, zakoreníme strom za \(c\) a dvakrát ho prejdeme pomocou dfs.
No počkať, ale strom pod \(c\) môže vyzerať inak pre rôzne korene, prečo môžeme mať všade rovnakú hodnotu \(L_v(c) = -1\)? Všimnime si, že stromy zodpovedajúce \(L_v(c)\) a \(L_u(c)\) sú izomorfné práve vtedy, keď sú izomorfné stromy zodpovedajúce \(L_c(v)\) a \(L_c(u)\) (cvičenie pre čitateľa). Vďaka tomu, že pre výpočet \(L_v(v)\) používame aj \(S_c(v)\), tak nám jedna hodnota \(L_v(c)\) nikdy nespraví problém.
A čo ak strom na vstupe nemá centrum? (T.j. priemer stromu má párnu dĺžku). V takom prípade je v strede jedinej najdlhšej cesty hrana. Do stredu tejto hrany pridáme nový vrchol, ktorý bude centrum. Vďaka tomu, že toto nové centrum je opäť unikátne (z hľadiska izomorfizmu), ostane všetko v poriadku. Ak v pôvodnom strome boli nejaké dva zakorenené stromy izomorfné, tak aj v strome s pridaným centrom budú izomorfné. Nesmieme však zabudnúť z výslednej odpovede odpočítať jednotku, lebo sme pridali jeden nový koreň, iný od všetkých ostatných.
Časová zložitosť riešenia je \(O(n \log n)\), ale podobne ako pri AHU algoritme, môžeme počítať labely po vrstvách, viď. popis AHU algoritmu vyššie, a dokážeme v lineárnom čase od počtu vrcholov na o jedna hlbšej vrstve spočítať všetky labely pre danú vrstvu. Takéto riešenie má časovú aj pamäťovú zložitosť \(O(n)\).
import random
import sys
sys.setrecursionlimit(1000000)
# read input
n = int(input())
E = [[] for _ in range(n)]
far_p = [0 for _ in range(n)]
for i in range(n - 1):
a, b = [int(x) - 1 for x in input().split()]
E[a].append(b)
E[b].append(a)
# find center
def farthest(v, parent):
far_p[v] = parent
f = (0, v)
for e in E[v]:
if e != parent:
ef = farthest(e, v)
f = max(f, (ef[0] + 1, ef[1]))
return f
perimeter, center = farthest(farthest(0, -1)[1], -1)
for i in range(perimeter // 2):
center = far_p[center]
# add virtual center if needed
if perimeter % 2:
a, b = center, far_p[center]
E[a].remove(b)
E[b].remove(a)
E.append([a, b])
E[a].append(n)
E[b].append(n)
center = n
n += 1
# solve
label_map = {}
def label(x):
x = tuple(x)
if x not in label_map:
label_map[x] = len(label_map)
return label_map[x]
S = [[] for _ in range(n)]
L = [0 for _ in range(n)]
def dfs_1(v, parent):
S[v] = [dfs_1(e, v) for e in E[v] if e != parent]
return label(sorted(S[v]))
def dfs_2(v, parent):
L[v] = -1 if parent < 0 else label(sorted(S[v] + [L[parent]]))
_ = [dfs_2(e, v) for e in E[v] if e != parent]
dfs_1(center, -1)
dfs_2(center, -1)
print(len(set(L)) - (perimeter % 2))Pri doprogramovaní si dávajte pozor, že vzorové riešenie v Pythone sa nemusí zmestiť do časového limitu, obzvlášť ak máte \(O(n\log n)\) časovú zložitosť. Vzorák v C++ zbehne s prehľadom a naše hashovacie riešenie v Pythone tiež v pohode prejde.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.