6. Interpol vzorové riešenie

2
5 7 1
10 13 1

-1

2
3 7 1
7 18 10

0

3
40 140 30
130 180 10
47 190 1

44.4827586207

Zamyslime sa najskôr nad statickou verziou tejto úlohy: ak máme daných \(n\) úsekov cesty \([ x_i,y_i]\), ako vyzerá ich prienik? Kedy je neprázdny?

Aby nejaký bod \(x\) patril do prieniku všetkých intervalov, museli už všetky začať, teda musí platiť \(x\geq\max_i x_i\). Tiež musí platiť, že žiaden interval ešte nesmel skončiť, teda \(x\leq\min_j y_j\).

Z toho vidíme, že môžu nastať dva prípady: ak \(\max_i x_i > \min_j y_j\), prienik je prázdny – niektorý interval skončí skôr ako niektorý iný začne. V opačnom prípade je prienik neprázdny a je ním zjavne práve uzavretý interval \([\max_i x_i, \min_j y_j]\).

Dĺžka intervalu ako funkcia

Ak si v našej úlohe zvolíme nejaký konkrétny okamih \(t\geq 0\), vieme si vypočítať, ako v danom okamihu vyzerajú slepé intervaly: \(i\)-ty z nich bude \([\ell_i + tv_i, r_i + tv_i]\).

Nás zaujíma, akú najdlhšiu dĺžku (a pre aké \(t\)) bude mať tento interval. Uvažujme preto nasledujúcu funkciu: \(f(t) = \min_j (r_j + tv_j) - \max_i (\ell_i + tv_i)\). Zjavne platí, že ak \(f(t) < 0\), tak je v čase \(t\) prienik prázdny, a inak \(f(t)\) udáva jeho dĺžku. Našu úlohu teda vieme preformulovať tak, že hľadáme, pre ktoré \(t\geq 0\) nadobúda funkcia \(f\) svoje maximum.

Príklad funkcie f

Na prvom grafe nižšie vidíme, ako sa tri rôzne slepé intervaly pohybujú v čase. Na \(x\)-ovej osi je čas, na \(y\)-ovej vzdialenosť na ceste. Znázornené intervaly zodpovedajú poslednému príkladu v zadaní, až na to, že \(\ell_2\) je o čosi väčšie, aby to lepšie vyzeralo.

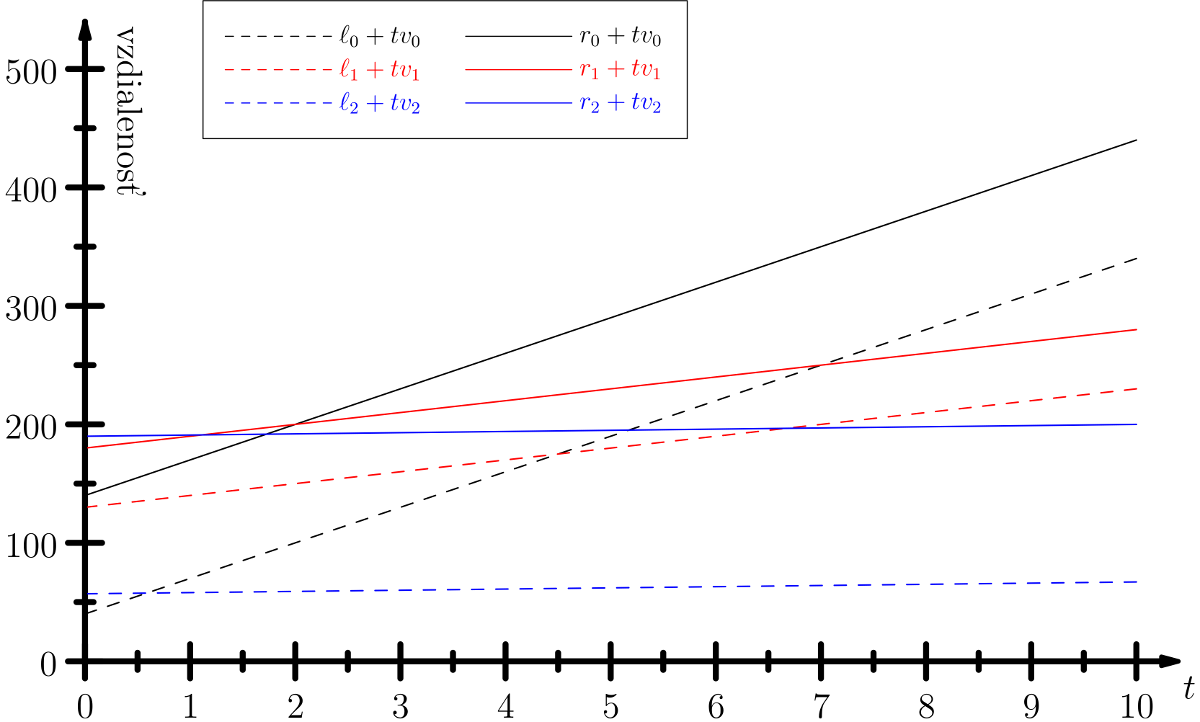
Čiarkované čiary predstavujú začiatky jednotlivých intervalov. Nás vždy zaujíma posledný začiatok (hodnota \(\max_i (\ell_i + tv_i)\)), čiže najvyššie sa nachádzajúca čiarkovaná čiara.

Analogicky nás v každom čase zaujíma prvý koniec intervalu, čiže najnižšie sa nachádzajúca plná čiara. Ak sa tá nachádza nad všetkými čiarkovanými, intervaly majú v danom čase neprázdny prienik.

Na druhom grafe sme vyfarbili oblasť, ktorá zodpovedá neprázdnemu prieniku intervalov, a hrubou čiarou sme vyznačili optimálne riešenie našej úlohy.

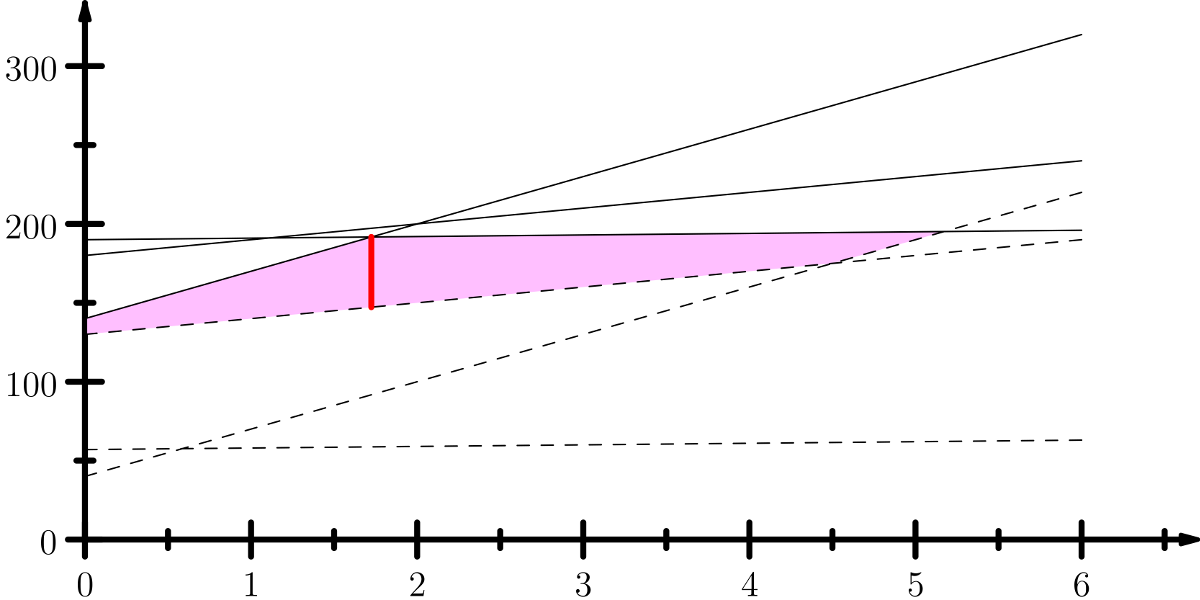
Dôležitá vlastnosť funkcie f

V čase \(t=0\) vidíme, že najvyššia čiarkovaná čiara zodpovedá intervalu 1, zatiaľ čo najnižšia plná čiara intervalu 0. No a keďže interval 0 sa hýbe rýchlosťou 30 a interval 1 len rýchlosťou 10, keď teraz pôjdeme v čase ďalej, bude dĺžka prieniku plynule rásť (rýchlosťou \(30-10 = 20\) za jednotku času).

V čase \(t=50/29\) sa spodnou plnou čiarou stane čiara zodpovedajúca intervalu 2. Ten sa hýbe len rýchlosťou 1. Od tohto okamihu ďalej teda bude čiarkovaná čiara plnú. Dĺžka prieniku sa teda bude meniť o \(1-10 = -9\) za jednotku času.

V čase \(t=9/2\) nastane ďalšia zmena: hornou čiarkovanou čiarou sa stane čiara zodpovedajúca intervalu 0. Od tejto chvíle sa dĺžka prieniku mení rýchlosťou \(1-30 = -29\) za jednotku času, a čoskoro už prienik prestane existovať.

Na tomto príklade si môžeme všimnúť všeobecné pravidlo, ktoré bude vždy platiť: rýchlosť, ktorou rastie dĺžka prieniku, sa môže s rastúcim časom . Totiž vždy, keď nastane zmena najvrchnejšej čiarkovanej čiary, tá nová rastie rýchlejšie, a vždy, keď nastane zmena najspodnejšej plnej čiary, tá nová rastie od tej predchádzajúcej pomalšie.

Keďže na začiatku môže byť rýchlosť rastu kladná, znamená to, že samotná (presnejšie, hodnota funkcie \(f\), ktorá nás zaujíma) vo všeobecnosti .

My teraz potrebujeme nájsť maximum takejto funkcie. Spravíme to binárnym vyhľadávaním.

Binárne vyhľadávanie

V ľubovoľnom čase \(t\) si vieme v čase \(O(n)\) nájsť aj najspodnejšiu plnú čiaru, aj najvrchnejšiu čiarkovanú, a u oboch sa pozrieť na to, ako rýchlo rastú. Rozdiel týchto dvoch hodnôt nám povie, či v danom bode funkcia \(f\) ešte rastie, je práve konštantná, alebo už klesá.

Začneme tým, že sa pozrieme na čas \(t=0\). Ak už v tomto okamihu \(f\) nerastie, je \(f(0)\) odpoveďou, ktorú hľadáme a môžeme skončiť.

Označme teraz \(m\) najväčšie číslo na vstupe (či už ide o súradnicu alebo rýchlosť). Pripomíname, že pre testovacie dáta platilo \(m\leq 10^6\). Potom tvrdíme, že po čase \(m\) už nenastane žiadna zmena: od tohto času ďalej musí byť aj čiarkovaná aj plná čiara stále tá istá. Totiž ak iná bola od nej rýchlejšie/pomalšie rastúca, tak na začiatku mala táto pred ňou najviac \(m\), a keďže sú všetky čísla celé, tá druhá čiara tento náskok dobiehala aspoň rýchlosťou 1 za jednotku času.

(Algebraicky, priesečník priamok \(a+bt\) a \(c+dt\), kde \(c\not= d\), je v bode \(t=(a-c)/(d-b)\), no a v základnom tvare má tento zlomok má čitateľ \(\leq m\) a menovateľ \(\geq 1\).)

Máme teraz dve pozorovania: v čase \(t_{lo}=0\) funkcia \(f\) ešte rastie, zatiaľ čo v čase \(t_{hi}=m\) už určite nerastie. Od tohto okamihu ďalej môžeme použiť spomínané binárne vyhľadávanie: dokola opakujeme, že sa pozrieme do stredu intervalu, vyhodnotíme, či tam \(f\) ešte rastie alebo už nerastie, a podľa toho posunieme buď \(t_{lo}\) alebo \(t_{hi}\).

Trocha technických detailov na záver

Pri praktickej implementácii si treba dať pozor na zaokrúhľovacie chyby. Hodnotu optimálneho \(t\), a teda aj hodnotu \(f(t)\), zistíme len približne. Zadanie síce sľubuje, že testovač je tolerantný, ale aj tak ostáva jeden okrajový prípad, na ktorý si treba dať pozor: ak je optimálna odpoveď presne \(f(t)=0\), ale správne \(t\) netrafíme presne, dostaneme ako \(f(t)\) hodnotu, ktorá je tesne pod nulou. Ak vtedy prehlásime, že riešenie neexistuje, dáme nesprávnu odpoveď.

V jednom autorskom riešení sme pre istotu celý záver riešenia spravili exaktne: po dostatočnom počte iterácií binárneho vyhľadávania máme nájdené nejaké \(t\). Okrem tohto \(t\) si exaktne (ako zlomok dvoch veľkých čísel) dopočítame najbližšie menšie aj najbližšie väčšie \(t\), v ktorom sa mení niektorá hraničná čiara, a v oboch časoch exaktne vyhodnotíme funkciu \(f\). Takto máme istotu, že sme určite našli optimálne riešenie.

Na úspešné vyriešenie úlohy však stačilo aj použitie reálnych (floating-point) čísel a vhodné zaokrúhľovanie. Správny čas \(t\), aj správna odpoveď je totiž vždy zlomok, ktorého menovateľ je najviac \(m\). V našom prípade to teda znamená, že ak je maximum \(f\) naozaj záporné, tak je vždy menšie alebo rovné \(-10^{-6}\). A teda ak nám vychádza odpoveď výrazne bližšia nule, môžeme si byť rozumne istí, že správnou odpoveďou je samotná nula.