Zadanie
Bola už hlboká noc, keď sa Jožko prebudil zo spánku. Sníval sa mu veľmi živý sen, z oblohy padali asteroidy, plné prerôznych krásnych kameňov1. Nadšený, úplne zabudol, že to bol iba sen, vyskočil z postele a vybehol von. Nočná obloha bola jasná, hviezdy svietili… a, čo to? Zreteľne padala hviezda. Jožko, ešte v papučiach, sa za ňou rozbehol, keď sa v tej tme potkol a spadol. Pozrel sa na zem a, čo nevidí? Kameň! To nemôže byť náhoda. Ako sa zahľadel zas na oblohu všimol si ďalší, zreteľne padajúci asteroid. Už nečakal a rozbehol sa za ním. V svetle mesiaca uvidel dopadnutý kameň, ešte krajší ako predchádzajúci, ale ako sa poň načahoval, rozplynul sa mu pred očami.
Zvláštne, pomyslel si Jožko. Skúšal zabehnúť ešte za pár kameňmi, ale polovicu nestihol, rozplynuli sa. Keďže je Jožko zvedavý chlapec, hneď sa rozhodol vyskúmať, ako to je s tými kameňmi. Napriek tomu, že bola hlboká noc, hackol sa do satelitných dát a vypočítal kedy, kde a aký2 kameň dopadne. Ostávajú posledné hodiny noci a Jožko sa zas vyberá na lov kameňov. Zaujímalo by ho, s akým úlovkom vie skončiť.
Úloha
Svet si vieme predstaviť ako priamku.
Na zem postupne spadne \(n\) (\(n \leq 500\,000\)) kameňov, \(i\)-tý z nich v čase \(t_i\), na mieste \(x_i\) a má hodnotu \(v_i\). Dva kamene môžu spadnúť na rovnaké miesto, alebo v rovnakom čase (nie však obe naraz). Pre jednoduchosť všetky časy sú v celých sekundách a súradnice v celých metroch. Kamene ostanú na mieste presne sekundu a potom sa rozplynú.
Jožko vie bežať jeden meter za sekundu. Na začiatku (v čase nula) stojí na súradnici \(p\). V prípade, že bude zbierať kamene optimálne, aký najväčší súčet hodnôt, ktorý vie získať?
Formát vstupu
Na prvom riadku sú dve medzerami oddelené čísla: \(n\), počet kameňov a \(p\), Jožkovú začiatočnú pozíciu.
V druhom riadku je \(n\) medzerami oddelených čísiel, \(t_1\) až \(t_n\), časy dopadu jednotlivých kameňov.
V treťom riadku je \(n\) medzerami oddelených čísiel, \(x_1\) až \(x_n\), miesta dopadu jednotlivých kameňov.
A na štvrtom riadku je \(n\) medzerami oddelených čísiel, \(v_1\) až \(v_n\) - hodnoty jednotlivých kameňov.
Je zaručené že dva kamene nedopadnú na rovnaké miesto v rovnaký čas.
Formát výstupu
Vypíšte dva riadky: na prvom, dve medzerami oddelené čísla - počet kameňov, ktoré Jožko v optimálnom prípade pozbiera a súčet ich hodnôt.
Na druhom riadku vypíšte čísla kameňov (číslo kameňa je jeho pozícia vo vstupe, číslované od nuly) ktoré má Jožko pozbierať, oddelené medzerou.
Ak existuje viac riešení, vypíšte ľubovoľné z nich.
Hodnotenie
Vaše programy budeme testovať na štyroch skupinách testovacích vstupov. Pre jednotlivé skupiny budú platiť nasledujúce obmedzenia:
| Skupina | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(1\leq n\leq\) | \(5\,000\) | \(100\,000\) | \(200\,000\) | \(500\,000\) |
| \(0\leq p, x_i, t_i\leq\) | \(10^9\) | \(5\,000\) | \(250\,000\) | \(10^9\) |
Vo všetkých vstupoch, \(0 < v_i \leq 10^9\)
Príklad
Input:
3 0
60 40 50
0 35 40
3 1 1Output:
1 3
0Input:
6 3
7 3 5 3 4 8
10 0 2 4 5 4
20 3 9 5 7 8Output:
3 22
2 5 3Jožkovi sa oplatí najskôr vziať kameň, ktorý spadne v tretej sekunde na mieste jedna, potom prebehnúť na doľava na kameň s hodnotou 9. Napokon sa prejde dva metre doprava a zoberie kameň s hodnotou 8. Takto získa kamene s hodnotou 22. Ak by sa rozhodol zobrať kameň s hodnotou 20, potom nevie zobrať iný kameň.
Input:
3 0
0 1 2
1 2 3
100 100 100Output:
0 0Jožko žiaľ nestihne dobehnúť pre žiadny z kameňov.
Kamene sú tu s nami už od doby KAMENnej a podnietili náš rozvoj v oblasti života. Bez nich by sme tu neboli, ale aj tak mám pocit, že nedostavajú také uznanie ako si zaslúžia. Kamene sú v mnohých ohľadoch (napr. tvrdosť, vytrvalosť, dĺžka života, zmysel pre humor, chuť, …) omnoho nadradenejšie ako my.↩︎
niektoré kamene sú lepšie ako iné↩︎
Málo kameňov
Ak je kameňov málo, vieme úlohu previesť na nasledovný podproblém:
Ak Jožko zoberie \(i\)-tý kameň, koľko najviac bodov vie odvtedy získať?
Riešenie je dynamické programovanie: Utrieďme si kamene podľa času dopadu a spracujme ich od najneskoršieho po najskorší. Pre každý už spracovaný kameň si zapamätáme hodnotu \(\text{best}_i\) - koľko najviac bodov vie získať Jožko od momentu keď zoberie tento kameň. Túto hodnotu pre \(i\)-tý kameň spočítame nasledovne: pozrime sa na všetky kameňe ktoré dopadli neskôr (pre ne sme už hodnotu spočítali). Takto zistíme ktoré má Jožko šancu zobrať a hodnota \(\text{best}_i\) je súčet hodnoty \(i\)-teho kameňa a maxima hodnôt pre dosiahnuteľné kamene.
Napokon si už len treba vybrať ktorým kameňom začneme. Na to stačí prejsť všetky kameňe a odpoveďou je maximum z \(\text{best}_i\).
Na zrekonštruovanie sekvencie si pre každý kameň stačí pamätať ktorý ďalší Jožko vezme.
Toto riešenie má časovú zložitosť \(O(n^2)\), pamäťovú \(O(n)\) a stačí na získanie \(2\) bodov z prvej sady.
Veľa kameňov, v malom časopriestore
Čo keď je kameňov veľa, ale sú roztrúsené po malom časopriestore? V druhej sade sa kameňe môžu vyskytovať iba prvých \(5000\) metrov a sekúnd. To je pomerne málo a vieme na tom založiť druhé riešenie dynamickým programovaním:
Pozrime sa na podproblém: Ak Jožko stojí v čase \(t\) na súradnici \(x\), aký najväčší súčet vie odvtedy (vrátane) dosiahnuť?
Spracujme hodnoty od neskorších časov ku skorším. Všimnime si, že na keď je Jožko na nejakej časopriestorovej súradnici, sú tri možnosti kde skončí o sekundu neskôr: buď sa posunie o jedno miesto doľava (\(x-1\)), o jedno doprava (\(x+1\)), alebo ostane na mieste. Pre každú súradnicu sa tak stačí pozrieť na tri ďalšie a z nich vziať maximum (a prípadne pričítať hodnotu kameňa, ak tam, kde stojíme, nejaký je).
Riešenie - maximálny súčet hodnôt ktoré vie pozbierať, je hodnota pre súradnicu \(t=0\), \(x=p\).
Rovnako ako v predchádzajúcom riešení, kamene ktoré Jožko vezme zrekonštruujeme tak, že že si pre každú súradnicu zapamätáme kde viedol optimálny krok.
Pre spočítanie zložitosti, označme \(X\) maximum z priestorových súradníc a \(T\) maximum časových súradníc. Časová aj pamäťová zložitosť je \(O(XT)\) a toto riešenie stačí pre ďalšie dva body z druhej sady.
Vzorové riešenie
Vzorové riešenie má myšlienku podobnú prvému riešenie hrubou silou - pre každý kameň si položíme otázku: aký najväčší súčet hodnôt môže Jožko získať od momentu ako zoberie \(i\)-tý kameň?
V riešení na prvú sadu sme si všetkých kandidátov po jednom prezreli, a vybrali maximum. Vyzerá to tak, že by to chcelo nejaký spôsob, ako rýchlo zistiť maximum z vhodnej množiny kameňov.
Predstavme si situáciu geometricky v časopriestore a zaznačme si z ktorých kameňov sa dá dostať na ktoré.
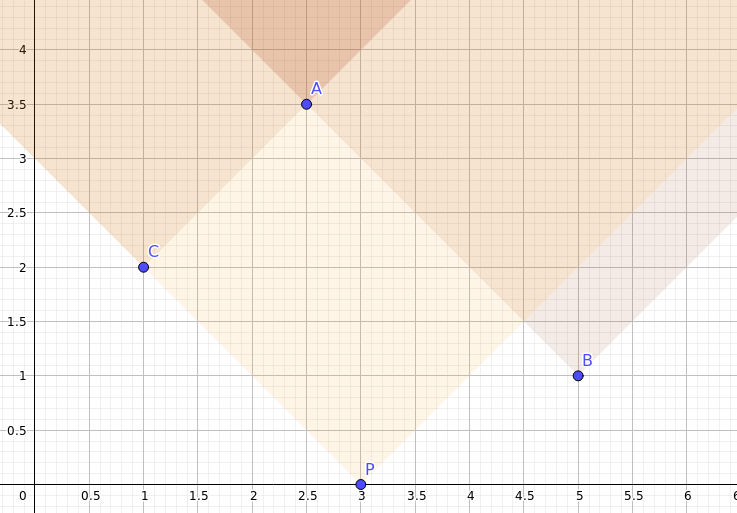
Všimnime si, že jednoduché pravidlo ako “ako ďalší kameň môžme vziať akýkoľvek, čo padne neskôr” nefunguje, napríklad na obrázku kameň B zo štartovnej pozície nie je dosiahnuteľný. Ak nájdeme pekné súradnice, v ktorom kritérium “viem zobrať tento kameň začínajúc na pozícii \((x, t)\)” sa dá vyjadriť ako interval problém by sa výrazne zjednodušil.
Na druhý pohľad si vieme všimnúť, že výsek časopriestoru do ktorého sa vieme od nejakého kameňu dostať je pravouhlý a ak kameň 1 leží vo výseku kameňa 2 a kameň 2 leží vo výseku kameni 3, tak kameň 1 leží vo výseku kameňa 3. Skúsme obrátiť súradnice o \(45\) stupňov:
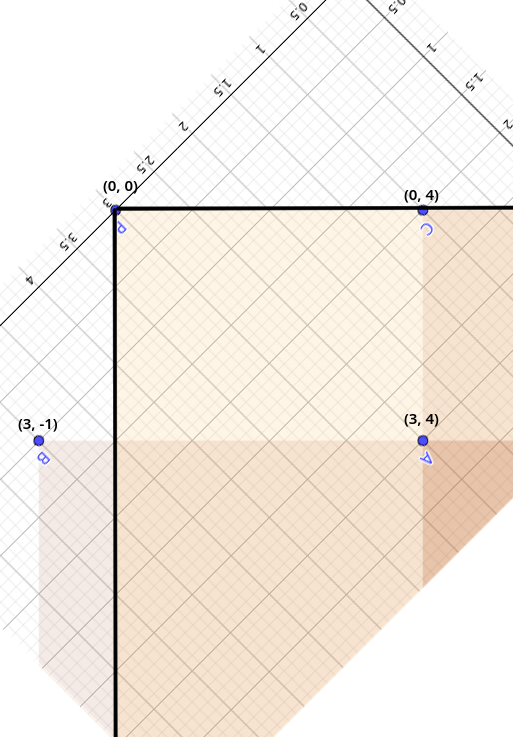
Môžme si všimnúť, že premenením súradníc na \((a, b)\)
\[ a = \frac{(x-p)+t}{2} \]
\[ b = \frac{t-(x-p)}{2} \]
Aby sme sa vyhli desatinným číslam, môžme vynechať delenie dvomi -
Dostaneme súradnice, v ktorých sa z \((a, b)\) vieme dostať na všetky body \((s, t)\) kde \(s \leq a\) a \(t \leq b\).
Teraz vieme úlohu riešiť pomocou intervalového stromu: spracujme kamene v poradí najskôr od najväčšieho \(a\) a potom od najväčšieho \(b\). Pri spracovaní kameňa na pozícii \((a, b)\) sa pozrieme do intervalového stromu na pozície od \(b\) väčšie a v logaritmickom čase zistíme ktorý kameň je optimálne vziať a koľko tak získame (potrebujeme obe tieto informácie). Následne uložíme informáciu o kameni na \(b\)-tú pozíciu do intervaláča.
Akú časovú zložitosť má toto riešenie? \(b\)-súradnica, ktorou indexujeme v intervaláči je ohraničená \(T\)-najväčším vyskytujúcim sa časom. Vytvoriť intervalový strom má lineárnu časovú i pamäťovú zložitosť, následné spracovanie každého kameňa \(\log T\) čas. Celková časová zložitosť je tým pádom \(O(T + n\log T)\). Toto riešenie by vyriešilo druhú a tretiu sadu a získalo by tak 4 body.
Pozorný čitateľ sa už isto čuduje? Nehovoril posledný nadpis vzorové riešenie? Pravdou je, že sme pri ňom už veľmi blízko - problém je veľkosť intervaláča - možný rozsah súradníc je rádovo viac, ako počet kameňov. Valná väčšina pozícií v intervalovom strome ostáva nevyužitá, ale spôsobuje TLEtie programu.
Riešenie na tento problém sa volá kompresia súradníc. Namiesto používanie \(b\) na indexovanie, prečíslujme súradnice ešte raz: zaujíma nás iba relatívne poradie (ktoré kamene majú nižšiu/vyššiu \(b\) súradnicu), takže nová druhá súradnica číslo “koľko z všetkých kameňov má nižšiu \(b\)-súradnicu ako ja?”. Toto číslo sa dá zistiť utriedením podľa \(b\)-súradnice v \(O(n\log n)\) čase.
Prečíslovanie spôsobí, že intervaláč bude mať veľkosť \(O(n)\) a teda sa časová zložitosť upraví na \(O(n\log n)\), pamäťová na \(O(n)\) a riešenie prejde na všetkých sadách.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.