Zadanie
Baklažán má konečne nový mobil. A nie hocijaký. Je to novučičký KSP Nokia Lumia S6, limitovaná edícia, s umelou inteligenciou na každom pixeli. Konečne totiž pochopil, že tie smartfóny sú v skutočnosti celkom užitočné, keď mu na starom mobile došla pamäť pri vkladaní nového kontaktu.
Jeho nový mobil sa mu ale bohužiaľ snaží dokázať opak: vyhadzuje jednu notifikáciu za druhou, s náhodnou informačnou hodnotou. Nemôže ich všetky ignorovať, lebo čo ak tá nasledujúca bude dôležitá? Už mu dochádza trpezlivosť… Koľko notifikácii ešte bude musieť dnes prečítať?
Úloha
Na začiatku nie sú na mobile žiadne neprečítané notifikácie. Následne prichádzajú tri typy udalostí:
- Aplikácia \(x\) vygenerovala jednu novú (neprečítanú) notifikáciu.
- Baklažán prečítal všetky (neprečítané) notifikácie od aplikácie \(x\).
- Baklažán prečítal prvých \(t\) neprečítaných notifikácii. Môžete predpokladať, že Baklažán má aspoň toľko neprečítaných notifikácii, ale môže ich mať aj viac.
Po každej udalosti vypíšte, koľko notifikácii je ešte neprečítaných. (Do toho sa nerátajú notifikácie, ktoré ešte neboli vygenerované.)
Formát vstupu
Na prvom riadku vstupu sú dve čísla oddelené medzerou: počet aplikácii \(n\) a počet udalostí \(q\). Platí \(1 \leq n, q \leq 500\,000\).
Každý z nasledujúcich \(q\) riadkov popisuje jednu udalosť. Popis udalosti má nasledovný formát: 1 <x>, 2 <x> a 3 <t> postupne pre udalosti prvého, druhého a tretieho typu. Platí \(1 \leq x \leq n\) (aplikácie číslujeme od \(1\)) a \(1 \leq t\).
Formát výstupu
Vypíšte \(q\) riadkov, na \(i\)-tom z nich nech je počet zostávajúcich notifikácii po \(i\)-tej udalosti.
Hodnotenie
Sú \(4\) testovacie sady, každá za \(2\) body. Platia v nich nasledovné obmedzenia:
| Sada | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(n, q \leq\) | \(500\) | \(5\,000\) | \(50\,000\) | \(500\,000\) |
Príklad
Input:
3 4
1 3
1 1
1 2
2 3Output:
1
2
3
2Input:
2 4
1 1
1 2
3 1
2 1Output:
1
2
1
1Pri tretej udalosti Baklažán prečíta notifikáciu aplikácie \(1\), nakoľko tá je prvá v poradí. Pri štvrtej udalosti nič neprečíta, lebo aplikácia \(1\) už nemá žiadne ďalšie notifikácie.
Input:
4 7
1 2
1 4
1 2
2 3
1 3
3 1
3 1Output:
1
2
3
3
4
3
2Pri štvrtej udalosti Baklažán nič neprečíta, lebo sa pozerá na aplikáciu \(3\), ktorá vtedy ešte nič nevygenerovala.
Jednoduchá simulácia
Neprečítané notifikácie si vieme predstaviť, že sú usporiadané do radu podľa toho, kedy prišli. Na začiatku radu sú najstaršie notifikácie, na konci najnovšie. Jednotlivé udalosti potom zodpovedajú nasledovným operáciám:
Keď príde nová notifikácia, tak ju umiestnime na koniec radu.
Keď prečítame všetky notifikácie od aplikácie \(x\), z radu vyhodíme všetky také notifikácie. Na to si potrebujeme pre každú notifikáciu pamätať, od ktorej aplikácie pochádza.
Keď prečítame prvých \(t\) notifikácii, z radu vyhodíme prvých \(t\) prvkov.
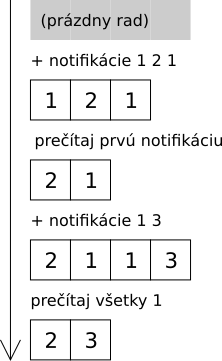
Náš rad je ale neštandardný, požadujeme totiž od neho nielen to, aby sme vedeli pridávať na koniec a mazať odpredu, ale aj to, aby sme vedeli mazať z vnútra radu. Ako to implementovať?
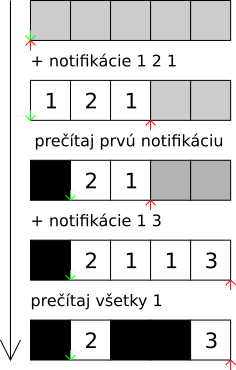
Aby sme vedeli pristupovať do vnútra radu, reprezentujeme si rad štandardne vo vnútri poľa.1 Máme dva smerníky: jeden na začiatok radu a jeden na koniec radu. Obsah radu je tvorený prvkami, ktoré sa v poli nachádzajú za začiatkom, ale pred koncom, pričom “za” chápeme cyklicky (za posledným políčkom poľa nasleduje prvé). Takýto rad vie mať iba toľko prvkov, koľko je dĺžka poľa. To nám ale nevadí: za celý život nám príde nanajvýš \(q\) notifikácii, stačí teda dĺžka poľa \(q\).
V takejto reprezentácii vieme pristupovať k prvkom radu. Čo ale keď chceme niektorý z nich zmazať? Stačí si pre jednotlivé prvky (t.j. políčka poľa) pamätať, či už boli zmazané alebo nie. Pri všetkých operáciách potom ignorujeme už zmazané prvky. - Ak chceme posunúť začiatok radu (napríklad lebo sme prečítali prvú \(1\) neprečítanú notifikáciu), tak preskočíme na prvý ešte-nezmazaný prvok. - Štandardne sa dĺžka radu dá vypočítať tak, že od seba odrátame pozície smerníkov na koniec a na začiatok radu, modulo dĺžka poľa. V tomto prípade ale nie všetky prvky medzi začiatkom a koncom skutočne sú v rade. Dĺžku radu si preto musíme explicitne počítať.
#include <iostream>
using namespace std;
int main () {
int n, q;
cin >> n >> q;
// implementacia radu
int pole[q];
int zac = 0, kon = 0;
bool zmazane[q];
for (int i = 0; i < q; i++) {
zmazane[i] = false;
}
int poc = 0;
for (int qi = 0; qi < q; qi++) {
int t, x;
cin >> t >> x;
if (t == 1) { // pridame prvok na koniec
pole[kon] = x;
kon += 1;
poc += 1;
}
else
if (t == 2) { // precitame vsetko od aplikacie <x>
for (int i = zac; i < kon; i++) {
if (zmazane[i]) {
continue;
}
if (pole[i] == x) {
zmazane[i] = true;
poc -= 1;
}
}
}
else { // precitame prvych <x> notifikacii
for (int xi = 0; xi < x; xi++) {
while (zmazane[zac]) {
zac += 1;
}
zmazane[zac] = true;
zac += 1;
}
poc -= x;
}
cout << poc << "\n";
}
return 0;
}V skutočnosti sa dá zaobísť aj bez operácie “zmaž prvok vo vnútri”. Pre záujemcov uvádzame zdrojový kód, skúste z neho sami vyčmuchať, že ako.
Zdrojové kódy budú zverejnené až po 17.6. 23:59:59. Dovtedy sa môžete pokúsiť úlohu naprogramovať sami
(a získať tým nejaké body navyše).Implementácia s použitím modernejších dátových štruktúr, ako je pole —použijeme dynamické pole std::vector.
#include <iostream>
#include <vector>
using namespace std;
int main () {
int n, q;
cin >> n >> q;
vector<int> notifikacie;
for (int i = 0; i < q; i++) {
int t, x;
cin >> t >> x;
if (t == 1) { // pridame prvok na koniec
notifikacie.push_back(x);
}
else
if (t == 2) { // precitame vsetko od aplikacie <x>
for (int j = 0; j < (int)notifikacie.size(); j++) {
if (notifikacie[j] == x) {
notifikacie.erase(notifikacie.begin() + j);
j--;
}
}
}
else { // precitame prvych <x> notifikacii
notifikacie.erase(notifikacie.begin(), notifikacie.begin() + x);
}
cout << notifikacie.size() << "\n";
}
return 0;
}Pamäťová zložitosť je \(O(q)\). Časová zložitosť sa ale ukáže byť až \(O(nq)\). Pozrime sa na zložitosti jednotlivých operácii nad radom.
Príchod novej notifikácie máme v čase \(O(1)\). Prečítanie prvých \(t\) notifikácii trvá v najhoršom prípade toľko, koľko je prvkov medzi smerníkom na začiatok a na koniec, takže na prvý pohľad táto operácia trvá dlho. Ak sa ale pozrieme na “big picture”, tak si uvedomíme, že pri tejto operácii sa nám smerník na začiatok vždy posunie v poli dopredu. Nikdy nepretečie, lebo notifikácii je len \(q\) a viac ich proste z radu nevyberieme. Pritom pole je dlhé tiež \(q\), teda sa tam všetky notifikácie zmestia. Takže dokopy nám tieto operácie tiež zaberú len \(O(q)\). 2
Problém ale nastáva, keď chceme prečítať všetky notifikácie niektorej aplikácie. Na to potrebujeme z radu vyhodiť nejaké vnútorné prvky—my postupne prejdeme všetky prvky radu, a o každom rozhodneme, či ho chceme alebo nie. Tento postup môže trvať až \(O(q)\), pričom niekedy za toľko veľa práce nemáme veľmi čo ukázať. Napríklad keď prečítame všetko od aplikácie \(1\), môže sa stať, že prejdeme celý rad dlhý \(O(q)\) a zistíme, že žiadna notifikácia od aplikácie \(1\) v ňom nie je. Spravili sme teda veľa práce, ktorú sme si možno mohli ušetriť.
Vzorové riešenie
Vyššie uvedená analýza nám hovorí, ktorú operáciu potrebujeme urýchliť: čítanie všetkých notifikácii niektorej aplikácie. Ak by sme si vedeli nejakým spôsobom pre každú aplikáciu pamätať, v ktorých políčkach poľa sú jej notifikácie, vyhrali by sme.
No ale to vieme spraviť, nie? Iba si pre každú aplikáciu udržujeme zoznam políčok, na ktorých sa nachádzajú jej notifikácie. - Keď príde nová notifikácia, tak príslušnej aplikácii na koniec zoznamu pridáme pozíciu v poli, kam notifikácia prišla. - Keď prečítame všetky notifikácie aplikácie, tak iba prejdeme tie prvky poľa, ktoré sú v jej zozname, a označíme ich za zmazané. Zoznam potom vyprádznime. - Čo ale, keď prečítame prvú neprečítanú notifikáciu? Celkom vhod nám príde, že je prvá—v zozname pre danú aplikáciu je teda určite na začiatku. Stačí je teda vymazať.
Od týchto zoznamov teda požadujeme len toľko, aby sme vedeli pridávať na koniec, prejsť cez všetky prvky, a mazať zo začiatku. Tieto požiadavky spĺňa (opäť) dátová štruktúra rad. Tentokrát na implementáciu ale nepoužijeme pole, nakoľko nemáme dobrý horný odhad na maximálnu veľkosť radu—určite v ňom bude nanajvýš \(q\) prvkov, avšak týchto zoznamov chceme \(n\), a \(nq\) pamäte je už veľa. Namiesto toho tieto rady implementujeme ako spájané zoznamy.
#include <iostream>
using namespace std;
// implementacia spajaneho zoznamu
struct Zoznam {
int pozicia;
Zoznam* dalsi;
Zoznam () : dalsi(NULL) {}
Zoznam (int poz0) : pozicia(poz0), dalsi(NULL) {}
};
int main () {
int n, q;
cin >> n >> q;
// implementacia radu
int pole[q];
int zac = 0, kon = 0;
bool zmazane[q];
for (int i = 0; i < q; i++) {
zmazane[i] = false;
}
int poc = 0;
// zoznamy pre jednotlive aplikacie
Zoznam* zaciatok[n+1];
Zoznam* koniec[n+1];
for (int i = 1; i <= n; i++) {
zaciatok[i] = NULL;
koniec[i] = NULL;
}
for (int qi = 0; qi < q; qi++) {
int t, x;
cin >> t >> x;
if (t == 1) { // pridame prvok na koniec
pole[kon] = x;
{ // upravime zoznam pre aplikaciu <x>
if (koniec[x] != NULL) {
koniec[x]->dalsi = new Zoznam(kon);
koniec[x] = koniec[x]->dalsi;
}
else {
zaciatok[x] = new Zoznam(kon);
koniec[x] = zaciatok[x];
}
}
kon += 1;
poc += 1;
}
else
if (t == 2) { // precitame vsetko od aplikacie <x>
Zoznam* kde = zaciatok[x];
while (kde != NULL) {
zmazane[kde->pozicia] = true;
Zoznam* dalsi = kde->dalsi;
delete kde; // v C++ nie je garbage collection, pamat si manazujeme sami...
kde = dalsi;
poc -= 1;
}
zaciatok[x] = NULL;
koniec[x] = NULL;
}
else { // precitame prvych <x> notifikacii
for (int xi = 0; xi < x; xi++) {
while (zmazane[zac]) {
zac += 1;
}
int ap = pole[zac];
Zoznam* dalsi = zaciatok[ap]->dalsi;
delete zaciatok[ap]; // v C++ nie je garbage collection, pamat si manazujeme sami...
zaciatok[ap] = dalsi; // zmazeme prvy prvok v zozname citanej aplikacie
if (zaciatok[ap] == NULL) {
koniec[ap] = NULL;
}
zmazane[zac] = true;
zac += 1;
}
poc -= x;
}
cout << poc << "\n";
}
return 0;
}Týmto sa nám podarilo zlepšiť časovú zložitosť druhej operácie. Opäť, jedna operácia môže trvať až \(O(q)\), ale keď sa pozrieme na big picture, zo zoznamu nemôžeme vybrať viac prvkov, ako do neho za celý život vložíme. Každá notifikácia príde len do jedného zoznamu, a teda dokopy vyberieme \(O(q)\) prvkov.3
Dostávame tak výslednú časovú zložitosť \(O(n + q)\) (potrebujeme \(O(n)\) na inicializáciu jednotlivých zoznamov).
Pre záujemcov zdrojový kód alternatívneho riešenia. Je celkom rovnaké, ako to predchádzajúce, až na to, že inak pristupuje k udalostiam tretieho typu. Skúste vyčmuchať, ako funguje a prečo má dobrú časovú zložitosť.
#include <iostream>
using namespace std;
// implementacia spajaneho zoznamu
struct Zoznam {
int pozicia;
Zoznam* dalsi;
Zoznam () : dalsi(NULL) {}
Zoznam (int poz0) : pozicia(poz0), dalsi(NULL) {}
};
int main () {
int n, q;
cin >> n >> q;
// implementacia radu
int pole[q];
int zac = 0, kon = 0;
bool zmazane[q];
for (int i = 0; i < q; i++) {
zmazane[i] = false;
}
int poc = 0;
// zoznamy pre jednotlive aplikacie
Zoznam* zaciatok[n+1];
Zoznam* koniec[n+1];
for (int i = 1; i <= n; i++) {
zaciatok[i] = NULL;
koniec[i] = NULL;
}
for (int qi = 0; qi < q; qi++) {
int t, x;
cin >> t >> x;
if (t == 1) { // pridame prvok na koniec
pole[kon] = x;
{ // upravime zoznam pre aplikaciu <x>
if (koniec[x] != NULL) {
koniec[x]->dalsi = new Zoznam(kon);
koniec[x] = koniec[x]->dalsi;
}
else {
zaciatok[x] = new Zoznam(kon);
koniec[x] = zaciatok[x];
}
}
kon += 1;
poc += 1;
}
else
if (t == 2) { // precitame vsetko od aplikacie <x>
Zoznam* kde = zaciatok[x];
while (kde != NULL) {
if (!zmazane[kde->pozicia]) {
zmazane[kde->pozicia] = true;
poc -= 1;
}
Zoznam* dalsi = kde->dalsi;
delete kde; // v C++ nie je garbage collection, pamat si manazujeme sami...
kde = dalsi;
}
zaciatok[x] = NULL;
koniec[x] = NULL;
}
else { // precitame prvych <x> notifikacii
for (int xi = 0; xi < x; xi++) {
while (zmazane[zac]) {
zac += 1;
}
zmazane[zac] = true;
zac += 1;
}
poc -= x;
}
cout << poc << "\n";
}
return 0;
}Viac o rade a príbuzných štruktúrach nájdete tu: https://www.ksp.sk/kucharka/stack_queue_deque/↩
Odbornými slovami, táto operácia zaberá čas \(O(1)\) amortizovane —niektoré jej volania síce budú trvať dlho, avšak dokopy to v priemere vyjde len \(O(1)\).↩
Amortizovane \(O(1)\).↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.