Zadanie
Tuhá zima už odišla, a tak majú farmári Slovakistanu plné ruky práce vysádzaním plodín na svojich poliach. Na veľké potešenie škodcov všetkého možného druhu, ktorí majú zas plné ústa práce ich vyjedaním.
Insektológ Kubík bol však odhodlaný svojim spoluobčanom pomôcť, a tak cez celé zimné prázdniny pracoval na revolučnom spôsobe, akým by sa škodci a polia dali vyjadriť číslami. Vďaka tomu by určite vedel poradiť farmárom, ako najlepšie ochrániť úrodu pred škodcami.
Svoj návrh predviedol pred KSP1, avšak neuspel – jeho abstraktné teórie boli síce fascinujúce, no keď prišlo na predvádzanie v praxi, ani so svojimi vytrénovanými kalkulačkovými schopnosťami nevedel dostatočne rýchlo odpovedať, ako najlepšie by sa dala ochrániť Slovakistanská úroda.
Kubík sa však nevzdal a poslal holuba do ďalekej krajiny, v ktorej vraj nažívajú šikovní programátori, ktorí by mu boli schopní pomôcť…
Úloha
Kubík každému škodcovi priradil prvočíslo – čím viac škody narobí, tým väčšie. Každému poľu potom vie priradiť číslo reprezentujúce škodcov, ktorí sa na ňom priživujú – prvočíslo každého prítomného škodcu umocní na mocninu zodpovedajúcu závažnosti zamorenia týmto škodcom a tieto mocniny potom vynásobí dokopy. Výsledné číslo budeme volať kontaminácia poľa. Prvočíselný rozklad kontaminácie poľa nám teda hovorí, ktoré druhy na poli škodia a mocniny jednotlivých prvočísel v rozklade poukazujú na závažnosť zamorenia. Navyše, kontaminácia poľa vyjadruje celkovú škodu, ktorú škodce na danom poli napáchajú.
Polia v Slovakistane sú všetky popri veľtoku Dujana. KSP vlastní lietadlo, ktorým vie postriekať súvislý úsek polí nejakým pesticídom, ktorý je špecificky určený na boj proti jednému druhu škodcov. Každý rok si lámu hlavu nad tým, ktoré pesticídy by mali kam nastriekať, aby zachránili čo najviac úrody.
Kubíkova teória na to však má odpoveď – keď postriekame pole pesticídom proti škodcovi s priradeným prvočíslom \(p\), kontamináciu tohto poľa vydelíme mocninou \(p\), ktorá je v jej rozklade. Rozdiel medzi originálnou a novou kontamináciou je potom množstvo úrody, ktoré sme vďaka pesticídu zachránili.
KSP má veľa návrhov, ktorý pesticíd kam nastriekať. Pre každý z nich povedzte, koľko úrody by tento zákrok zachránil.
Formát vstupu
V prvom riadku sú tri čísla \(n\), \(q\) a \(p\) – počet polí v Slovakistane, počet návrhov kam nastriekať pesticíd, a najväčšia možná kontaminácia poľa.
V druhom riadku vstupu je \(n\) kladných celých čísel \(v_1, v_2, \dots, v_n\) (\(1 \leq v_i \leq p\)) – hodnoty kontaminácie jendotlivých polí, v poradí v akom sú popri veľtoku Dujana.
Nakoniec nasleduje \(q\) riadkov s tromi číslami \(l_i, r_i, p_i\). Tieto tri čísla popisujú návrh KSP, aby sa všetky polia od \(l_i\)-tého až po \(r_i\)-té (vrátane) postriekali pesticídom proti škodcovi s číslom \(p_i\). Platí \(1 \leq l_i \leq r_i \leq n\) a \(1 \leq p_i \leq p\). Číslo \(p_i\) je vždy prvočíslo.
Formát výstupu
Pre každý návrh povedzte, koľko úrody by bolo zachránenej, ak by sa vykonal. Formálne, povedzte o koľko by sa zmenil súčet čísel \(v_{l_i} + \dots + v_{r_i}\), ak by sme každé vydelili tou mocninou prvočísla \(p_i\), ktorá sa v ňom nachádza.
Hodnotenie
Pre jednotlivé testovacie sady platia nasledovné obmedzenia:
| číslo sady | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|
| \(n,q \leq\) | \(1\,500\) | \(100\,000\) | \(100\,000\) | \(300\,000\) |
| \(p \leq\) | \(10^6\) | \(100\) | \(10^6\) | \(10^6\) |
Upozorňujeme, že riešenia v pomalých jazykoch, ako Python, nemusia stíhať.
Príklady
Input:
5 5 100
10 20 30 40 50
1 1 2
1 5 5
1 5 47
2 4 3
2 4 2Output:
5
128
0
20
65V štvrtom návrhu dostávame rozdiel súčtu \((20+30+40)-(20+10+40) = 20\).
Komisia Slovakistanského Poľnohospodártsva↩
Stará dobrá hrubá sila
Ako inak, úloha sa dá riešiť aj hrubou silou. Pre každú otázku prejdeme zadaný interval, každé číslo delíme daným prvočíslom kým to len ide, a k odpovedi pripočítame rozdiel pôvodného a výsledného čísla.
Aká je časová zložitosť? Pre každú otázku prejdeme najviac \(n\) čísel a každé z nich niekoľkokrát vydelíme–najviac ale logaritmicky veľakrát, a kedže všetky čísla v poli sú nanajvýš \(p\), budeme deliť \(O(\log p)\)-krát.
Každá otázka nám teda zaberá \(O(n \log p)\) času, a teda \(q\) otázok zodpovedáme v \(O(qn \log p)\), a tešíme sa, že prejdeme prvou sadou. Otázky môžeme riešiť po jednej, a teda si okrem zamorení polí pamätáme len konštantne veľa premenných; pamäťová zložitosť je teda \(O(n)\).
#include <iostream>
using namespace std;
int main()
{
int n,q,p;
cin >> n >> q >> p;
int polia[n];
for(int i=0;i<n;++i)
cin >> polia[i];
while(q--)
{
int l,r,p;
cin >> l >> r >> p;
int res = 0;
for(int i=l-1;i<r;++i)
{
int x = polia[i];
while(x%p==0)
x /= p;
res += polia[i]-x;
}
cout << res << "\n";
}
}Všetko si predpočítame
Chceli by sme zrýchliť odpovedanie na otázky, nakoľko \(O(n \log p)\) si okrem prvej sady nemôžeme nikde dovoliť.
Ako by vyzerala úloha, keby každá otázka bola o rovnakom prvočísle \(x\)? Každá kontaminácia poľa \(v_i\) by (ak je v intervale otázky) prispela nejakou hodnotou \(x_i\), ktorá sa nikdy nezmení. Každá otázka by teda bola priamočiaro ‘súčet čísel v intervale’, ktoré vieme v \(O(1)\) zodpovedať pomocou prefixových súčtov.
Môžeme si teda predpočítať prefixový súčet hodnôt \(x_i\) pre každé prvočíslo \(x\) menšie rovné \(p\). Takýto prístup je dosť efektívny na druhú sadu, kde \(p\) je malé.
Pre ilustráciu, hodnoty \(x\) v príkladovom vstupe by vyzerali takto:
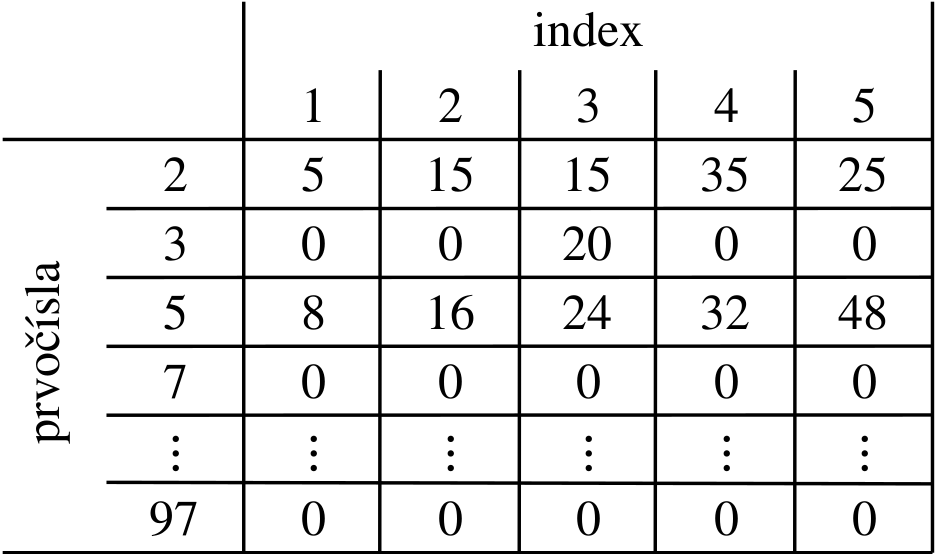
A k nim prislúchajúce prefixové súčty:
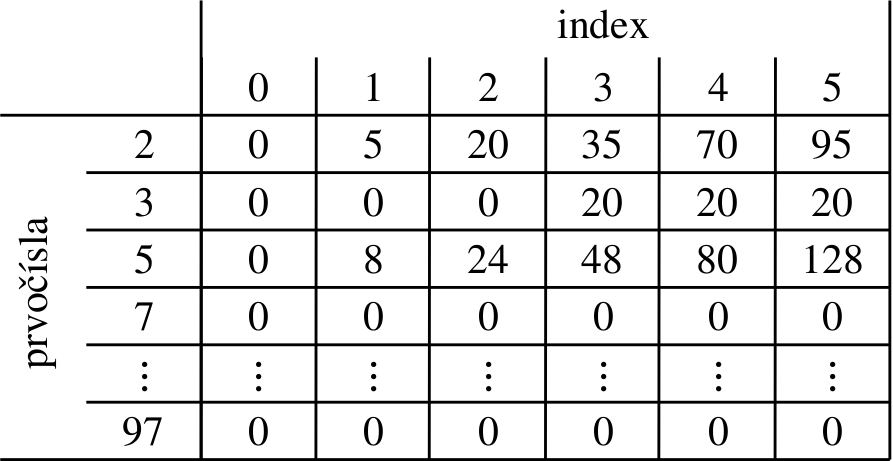
Aká je teda časová zložitosť? V čase \(O(p^{3/2})\) vieme nájsť všetky prvočísla do \(p\)—iba pre každé číslo \(2, 3, \ldots, p\) overíme, či má deliteľa menšieho/rovného jeho odmocnine. Potom pre každé prvočíslo vypočítame hodnoty \(x\). Všetkých hodnôt \(x\) je \(O(np)\)1. Na výpočet každej z hodnôt \(x\) potrebujeme \(O(\log p)\)-krát deliť, teda toto predpočítanie nám potrvá \(O(np \log p)\). Otázky už zodpovedáme v \(O(1)\). Časová zložitosť je teda \(O(np \log p + q)\).
Pamäťová zložitosť je \(O(np)\), nakoľko si pamätáme prefixové súčty hodnôt \(x\).
#include <bits/stdc++.h>
using namespace std;
vector<int> najdi_prvocisla(int MAX)
{
vector<int> prvocisla;
for(int i=2;i<=MAX;++i)
{
bool ok = true;
for(int j=2;ok && j*j<=i;++j)
if(i%j==0)
ok = false;
if(ok) prvocisla.push_back(i);
}
return prvocisla;
}
int main()
{
int n,q,p;
cin >> n >> q >> p;
if(n<=1500 && q<=1500)
{
//riesenie hrubou silou
return 0;
}
vector<int> prvocisla = najdi_prvocisla(p);
vector<int> ocislovanie(p+1);
for(int i=0;i<prvocisla.size();++i)
ocislovanie[ prvocisla[i] ] = i;
vector<vector<int>> prefix(prvocisla.size(),{{0}});
for(int i=0;i<n;++i)
{
int v;
cin >> v;
for(int j=0;j<prvocisla.size();++j)
{
int tmp = v;
while(tmp%prvocisla[j] == 0)
tmp /= prvocisla[j];
prefix[j].push_back(v-tmp+prefix[j][i]);
}
}
while(q--)
{
int l,r,pi;
cin >> l >> r >> pi;
pi = ocislovanie[pi];
cout << prefix[pi][r] - prefix[pi][l-1] << "\n";
}
}Predpočítame len nenulové prvky
Vo vyššieuvedenom riešení už odpovedáme na otázky dosť rýchlo, pridlho nám však trvá predpočítanie prefixových polí. Máme v nich priveľa prvkov, potrebujeme ich ale všetky?
Musíme si uvedomiť, že tak, ako v čísle veľkosti \(p\) môže byť prvočíslo umocnené na najviac \(\log p\), tak isto v ňom môže byť najviac \(\log p\) rôznych prvočísel. Príkladne pre \(p = 10^6\) máme 78498 prvočísel, avšak v konkrétnom čísle do \(10^6\) ich vie najviac byť len 72! Pre každé z \(n\) čísel nám teda reálne najviac \(\log p\) hodnôt \(x\) dodalo nejakú podstatnú informáciu, zvyšné sú nutne nuly. Stačí nám teda uvažovať len týchto \(n \log p\) hodnôt, a pre každú si navyše pamätáme, ktorému indexu zodpovedá.
Pre ilustráciu, hodnoty \(x\) v príkladovom vstupe by sa skomprimovali takto:

(Prvé číslo je index \(i\), druhé je hodnota \(x_i\).) Keď máme (komprimované) hodnoty \(x\), ľahko k nim zostrojíme (komprimované) prefixové súčty. V príkladovom vstupe be sme dostali:

Žiadne ďalšie prvočísla v číslach na vstupe neboli, teda zvyšné prefixové súčty sú (efektívne) prázdne.
Keď už poznáme prefixové súčty, na každú otázku vieme odpovedať nasledovne. Ak chceme súčet intervalu \(\langle l_i, r_i \rangle\), nájdeme v príslušnom prefixovom poli prvé \(L_i \geq l_i\) a posledné \(R_i \leq r_i\), a odpovieme súčtom v \(\langle L_i, R_i \rangle\) (ktorý je rovnaký). Tieto dve hodnoty vieme binárne vyhľadať v \(O(\log n)\), zodpovedanie všetkých otázok nám teda bude trvať \(O(q \log n)\).
Ostáva teda len jedna otázka: ako rýchlo si vieme hodnoty \(x\) predpočítať?
Budeme postupovať podobne, ako pri Eratostenovom site. Upravíme ho tak, aby nám navyše pre každé číslo našlo najmenšie prvočíslo, ktoré ho delí—vždy, keď zistíme, že nejaké \(q\) je prvočíslo, navštívime všetky násobky \(q\). Všetky násobky, ktoré sme doteraz nenavštívili, určite nie sú deliteľné žiadnym prvočíslom menším ako \(q\), ich najmenší prvočíselný deliteľ je teda \(q\).
Tak, ako pri štandardnom Eratostenovom site, stačí nám navštíviť len tie násobky, ktoré sú väčšie alebo rovné ako \(q^2\). Menšie násobky sú totiž deliteľné aj nejakým prvočíslom menším ako \(q\), ktoré sme už spracovali—a teda už poznáme najmenšieho prvočíselného deliteľa takého násobku.
Toto spravíme v čase \(O(p \log \log p)\) a pamäti \(O(p)\).
Keď teraz chceme zistiť prvočíselný rozklad nejakého \(v_i\), budeme ho zakaždým deliť jeho najmenším prvočíselným deliteľom, až kým nedosiahne hodnotu \(1\). Pritom si pamätáme, ktorými prvočíslami sme ho vydelili a koľkokrát. Každé zistenie rozkladu nám bude trvať \(O(\log p)\).
Z rozkladu \(v_i\) následne zostrojíme komprimovanú tabuľku hodnôt \(x\) v čase \(O(n \log p)\), a zostrojíme komprimované prefixové súčty v čase lineárnom od veľkosti tabuľky, čiže tiež \(O(n \log p)\). Nakoniec v \(O(q \log n)\) zodpovieme otázky.
Spolu s Eratostenovým sitom dostávame časovú zložitosť \(O(p \log \log p + n \log p + q \log n)\). Pamäťová zložitosť je \(O(p + n \log p)\), nakoľko si pamätáme pole s najmenšími prvočíselnými deliteľmi, a prefixové súčty hodnôt \(x\).
#include <bits/stdc++.h>
using namespace std;
#define NEZNAMY -1
int p;
vector<int> ocislovanie;
vector<int> min_prvodelitel;
vector<int> prvocisla;
vector<vector<pair<int,long long> > > prefixy;
void Eratosten()
{
for(int i=2;i<=p;++i)
{
if(min_prvodelitel[i] != NEZNAMY)
continue;
prvocisla.push_back(i);
ocislovanie[i] = prvocisla.size()-1;
min_prvodelitel[i] = i;
if((long long)i*i >= p) continue;
for(int k=i*i;k<=p;k+=i)
if (min_prvodelitel[k] == NEZNAMY)
min_prvodelitel[k] = i;
}
prefixy.resize(prvocisla.size(),{{0,0}});
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,q;
cin >> n >> q >> p;
min_prvodelitel.resize(p+1, NEZNAMY);
ocislovanie.resize(p+1);
// najdeme prvocisla <= p
// a pre cisla <= p ich najmensich prvociselnych delitelov
Eratosten();
for(int i=0;i<n;++i)
{
int v,tmp;
cin >> v;
tmp = v;
// najdeme prvociselnych delitelov v
vector<int> prvodelitelia;
while(tmp != 1)
{
int pdel = min_prvodelitel[tmp];
if (prvodelitelia.empty() || pdel != prvodelitelia.back())
prvodelitelia.push_back(pdel);
tmp /= pdel;
}
// pre kazdeho prvociselneho delitela v najdeme prislusnu hodnotu x
for(int k=0;k<(int)prvodelitelia.size();++k)
{
int pdel = prvodelitelia[k];
tmp = v;
while(tmp % pdel == 0)
tmp /= pdel;
// pridame prvok do prefixoveho suctu s indexom cisla, a kolko urody zachrani
prefixy[ocislovanie[pdel]].push_back({i+1,v-tmp});
}
}
for(int i=0;i<prvocisla.size();++i)
{
for(int k=1;k<prefixy[i].size();++k)
prefixy[i][k].second += prefixy[i][k-1].second;
}
while(q--)
{
int l,r,p;
cin >> l >> r >> p;
p = ocislovanie[p];
//L = posledny prefix s indexom < l, R = posledny prefix s indexom <= r
int L,R;
int low=0,high=prefixy[p].size();
// binarne vyhladame posledny prefix s indexom < l
while(high-low>1)
{
int mid = (high+low)/2;
if(prefixy[p][mid].first < l)
low = mid;
else high = mid;
}
L = low;
low=0,high=prefixy[p].size();
// binarne vyhladame posledny prefix s indexom <= r
while(high-low>1)
{
int mid = (high+low)/2;
if(prefixy[p][mid].first <= r)
low = mid;
else high = mid;
}
R = low;
cout << prefixy[p][R].second - prefixy[p][L].second << "\n";
}
}Dá sa dokázať, že prvočísel v \(1, \ldots, p\) je \(O(\frac{p}{\log p})\), a tým sa dá odhad vylepšiť na \(O(n \cdot \frac{p}{\log p})\). Záujemcovia môžu navštíviť https://en.wikipedia.org/wiki/Prime_number_theorem↩
\(2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 = 510\,510\). Použili sme tu čo najmenšie prvočísla, a ôsme už do milióna nezmestíme.↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.