4. Dievčatá sú náročné vzorové riešenie

AND(X,OR(X,X))

3

NOT(OR(X,X))

1

Našou úlohou bolo zistiť, koľkými spôsobmi vieme doplniť premenné tak, aby bol zadaný logický výraz pravdivý. Pri takýchto úlohach je fajn sa ako prvé zamyslieť nad tým, ako sa dá tento výraz reprezentovať v pamäti.

Ako výraz reprezentovať

Výraz obsahuje mnoho zátvoriek a v nich ďalšie výrazy. Každú logickú spojku alebo premennú si vieme reprezentovať ako vrchol v strome. (Ak vám slovíčko “strom” v súvislosti s informatikou nič nehovorí, odporúčam prečítať si časť o stromoch tu.) V tomto strome má každý vrchol buď \(0\), \(1\) alebo \(2\) synov—vrcholy reprezentujúce výrazy (operandy), ktoré sú v jeho zátvorkách.

Napríklad OR(X_1, NOT(X_2)) reprezentujeme vrcholom pre OR, ktorý má ako synov vrcholy X_1 a NOT. Tento NOT má syna X_2.

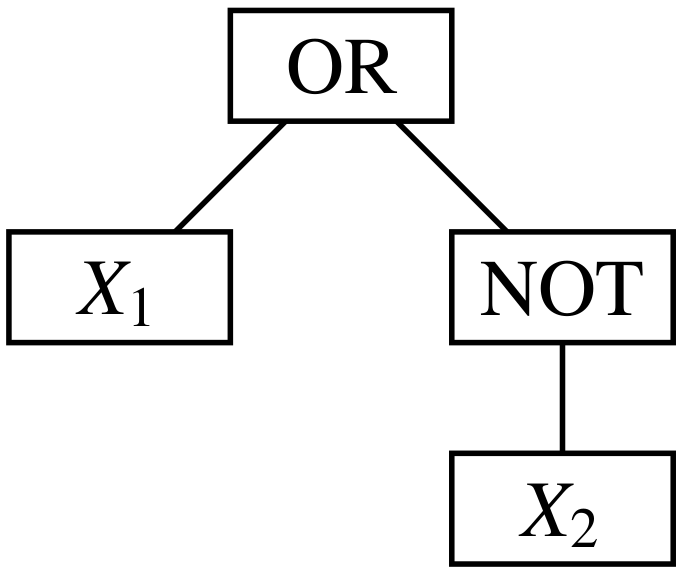
Otázka je, ako z textovej reprezentácie výrazu dostaneme takýto strom? Budeme ho zostrojovať rekurzívne, od koreňa k listom. Predstavme si, že text čítame zľava doprava. Na začiatku sa určite nachádza jedna zo značiek AND, OR, NOT alebo X. Podľa toho, ktorý z týchto prípadov nastal, vieme, čo máme ďalej v texte očakávať:

• Ak sme prečítali AND alebo OR, bude nasledovať (, výraz, ,, výraz, ). Takže stačí rekurzívne načítať prvý operand, prečítať čiarku ,, načítať druhý operand a prečítať koncovú zátvorku ). Vrátime vrchol príslušného typu, ktorého synovia sú načítané operandy.
• Ak sme prečítali NOT, postupujeme podobne. Jediný rozdiel je v tom, že máme len jeden operand a nemusíme prečítať čiarku.
• Ak sme prečítali X, vrátime vrchol reprezentujúci premennú.

Keď máme načítaný vstup a uložený v strome, vieme sa vrhnúť na prvé riešenie.

Ako vieme nájsť ohodnotenie výrazu

Všimnime si, že ak máme vyhodnotených všetkých synov nejakého vrcholu, tak vieme v konštantnom čase zistiť ohodnotenie tohto vrcholu. Toto tvrdenie nie je nejako závratné, spočíva len v tom, že spočítame hodnotu logickej funkcie v tomto vrchole. Z tohto tvrdenia ale vyplýva dôležitejšie—predstavme si, že poznáme hodnoty všetkých listov (premenných). Potom vieme v lineárnom čase zistiť hodnotu celého výrazu.

Spravíme to takto: ak chceme vyhodnotiť nejaký vrchol, vyhodnotíme najprv všetkých jeho synov a následne v konštantnom čase vyhodnotíme logickú funkciu z hodnôt synov. Vieme, že listy už máme ohodnotené, takže ak to budeme vyhodnocovať rekurziou, má kde zastať. Takémuto algoritmu to bude trvať \(O(n)\), kde \(n\) bude počet vrcholov. Toto môžeme jednoducho odhadnúť ako dĺžku vstupu. Pre každý vrchol spravíme iba konštantný počet operácii.

Nás zaujíma počet takých ohodnotení, pri ktorých je vstupný výraz pravdivý. Môžeme vyskúšať všetky možné ohodnotenia, pre každé zistiť hodnotu celého výrazu a spočítať tie, ktoré sú pravdivé. Všetkých možností ohodnotenia máme najviac \(2^n\) a teda časová zložitosť riešenia je \(O(n \cdot 2^n)\).

Týmto riešením mohol váš program získať \(2\) body.

Vzorové riešenie

Skúsme si náš problém vyriešiť pre najmenšie možné stromy.

Pre strom skladajúci sa z jedného X máme práve jednu možnosť ako môže byť pravdivý: ak za X dosadíme \(1\).

Pokiaľ máme strom NOT(X), je práve jedna možnosť ako môže byť pravdivý: ak X je nepravdivé. Všeobecne, počet možnosťí ako môže byť NOT(výraz) pravdivý je počet možností, ako môže byť výraz nepravdivý. Pre strom OR(X,X) máme tri dosadenia, ako získať pravdivý výraz: \((0,1)\) , \((1,0)\) a \((1,1)\). Pre strom AND(X,X) je zasa len jedno: \((1,1)\).

Pri vyhodnocovaní NOT sme si všimli zaujímavú vec: ak by sme vedeli, koľkými spôsobmi môžu byť jeho synovia nepravdivý, vedeli by sme hneď povedať, koľkými spôsobmi môže byť NOT pravdivý. Myšlienka, ktorá nás môže napadnúť je, či sa toto nedá použiť aj pre ostatné typy vrcholov.

Poďme teda skúsiť vyhodnotiť AND(výraz1, výraz2) s tým, že pre výraz1 aj výraz2 vieme, koľkými spôsobmi môžu byť pravdivé. Označme tieto počty postupne \(p_1\) a \(p_2\). Hľadáme počet možností, v ktorých sú aj výraz1 aj výraz2 pravdivé. Tí, čo už mali trocha kombinatoriky hneď vidia, že to je \(p_1 \cdot p_2\)—pre každú možnosť, v ktorej je výraz1 pravdivý, existuje \(p_2\) možností, v ktorých je aj výraz2 pravdivý.

Kebyže vieme, koľkými spôsobmi možu byť výraz1 a výraz2 nepravdivé, vieme zistiť dokonca aj to, koľkými spôsobmi môže byť AND(výraz1, výraz2) nepravdivý. Označme si teda \(n_1\) a \(n_2\) počty nepravdivých možností pre vyrazy 1 a 2. AND(výraz1, výraz2) je nepravdivý v troch prípadoch

• výraz1 je nepravdivý a výraz2 je nepravdivý: \(n_1 \cdot n_2\) možností
• výraz1 je pravdivý a výraz2 je nepravdivý: \(p_1 \cdot n_2\)
• výraz1 je nepravdivý a výraz2 je pravdivý: \(n_1 \cdot p_2\)

Teda AND je nepravdivý v toľkoto prípadoch:

\[n_1 \cdot n_2 + p_1 \cdot n_2 + n_1 \cdot p_2.\]

Rovnakým spôsobom vieme vymyslieť, ako z počtov možností detí vrcholu OR zistiť počty možností samotného vrcholu OR.

Takže ak vieme, koľkými spôsobmi vedia byť deti nejakého vrcholu pravdivé a koľkými spôsobmi vedia byť nepravdivé, vieme zistiť aj pre tento samotný vrchol rovnakú informáciu. Použijeme pri tom len pomocou pár násobení v prípade AND a OR, a výmenou hodnôt v prípade NOT. A o listoch stromu vieme, že je práve jedna možnosť ako môžu byť pravdivé, a práve jedna ako môžu byť nepravdivé.

Tu si zoberieme myšlienku z brute forcu—keď sme chceli zistiť vyhodnotenie stromu s nejakými hodnotami vrcholov, rekurzívne sme ho prešli a pre každý vrchol sme z jeho synov zistili jeho hodnotu. V našom riešení môžme spraviť to isté, len pre každý vrchol zo synov zistíme, koľkými spôsobmi môže byť pravdivý a koľkými nepravdivý. Riešenie bude potom počet pravdivých spôsobov pre koreň.

Časová zložitosť je \(O(n)\), keďže pre každý vrchol v konštantom čase zistíme jeho hodnotu. Pamäťová je \(O(n)\), nakoľko si pamätáme celý strom.

#include <string>
#include <cstdio>
#include <cstdlib>
#include <iostream>

const long long MOD = 1000000007L;
using namespace std;

typedef long long ll;

enum typ{
    PREM,
    OR,
    AND,
    NOT
};

struct Node{
    typ t;
    Node * c[2];
    ll fa = 0;
    ll tr = 0;
};

Node * parse(const string &s, int & pos){
    Node * x = new Node;
    if(s[pos] == 'X'){
       x-> t = PREM;
       pos += 1;
    }
    else if(s[pos] == 'A'){
       x->t = AND;
       pos += 4;
       x->c[0] = parse(s,pos);
       pos+=1;
       x->c[1] = parse(s,pos);
       pos +=1;
    }
    else if(s[pos] == 'O'){
       x->t = OR;
       pos += 3;
       x->c[0] = parse(s,pos);
       pos+=1;
       x->c[1] = parse(s,pos);
       pos +=1;

    }
    else if(s[pos] == 'N') {
       x->t = NOT;
       pos += 4;
       x->c[0] = parse(s,pos);
       pos +=1;
    }
    return x;
}

void pocetMoznosti(Node * x){
    switch(x->t){
        case PREM:
            x->tr = 1;
            x->fa = 1;
            break;
        case OR:
            pocetMoznosti(x->c[0]);
            pocetMoznosti(x->c[1]);
            x->fa = x->c[0]->fa * x->c[1]->fa;
            x->tr = x->c[0]->tr*(x->c[1]->tr + x->c[1]->fa) + x->c[0]->fa *x->c[1]->tr;
            break;
        case AND:
            pocetMoznosti(x->c[0]);
            pocetMoznosti(x->c[1]);
            x->tr = x->c[0]->tr * x->c[1]->tr;
            x->fa = x->c[0]->fa * (x->c[1]->tr + x->c[1]->fa) + x->c[0]->tr*x->c[1]->fa;
			x->tr %= MOD;
			x->fa %= MOD;
            break;
        case NOT:
            pocetMoznosti(x->c[0]);
            x->tr = x->c[0]->fa;
            x->fa = x->c[0]->tr;
    }
	x->tr %= MOD;
	x->fa %= MOD;
}


int main(){
    string s;
    cin >> s;

    int parser=0;
    Node * x = parse(s,parser);
    pocetMoznosti(x);
    printf("%lld\n",x->tr);
}