Zadanie
Iste každý už počul o rieke Ipeľ. Ak si myslíte, že sa jedná o nejakú riečku na juhu Slovenska, tak ste ne omyle. Totiž každý južan (vrátane mňa) si pamätá, ako sa veľtok Ipľu vylial. Záplavy zasiahli aj naše mesto a zničili v ňom bohatú infraštruktúru1.
V posledných rokoch je však obodbie sucha, a tak veľa ľudí zabúda na toto nebezpečenstvo. Túto zimu mi však istá nemnovaná osoba (Iľko) dala info, že Ipeľ sa vyleje. Ľadové kryhy, ktoré vzniknú pri výkyvoch teploty, totiž upchajú jeho koryto.
Keď teda vieme, že nastane katastrofa, musíme sa pripraviť. Vieme, že vysoké budovy v našom meste zastavia vodu. Máme mapu mesta, na ktorej sú tieto budovy vyznačené. Zaujíma nás, koľko územia ostane nezaplaveného.
Úloha
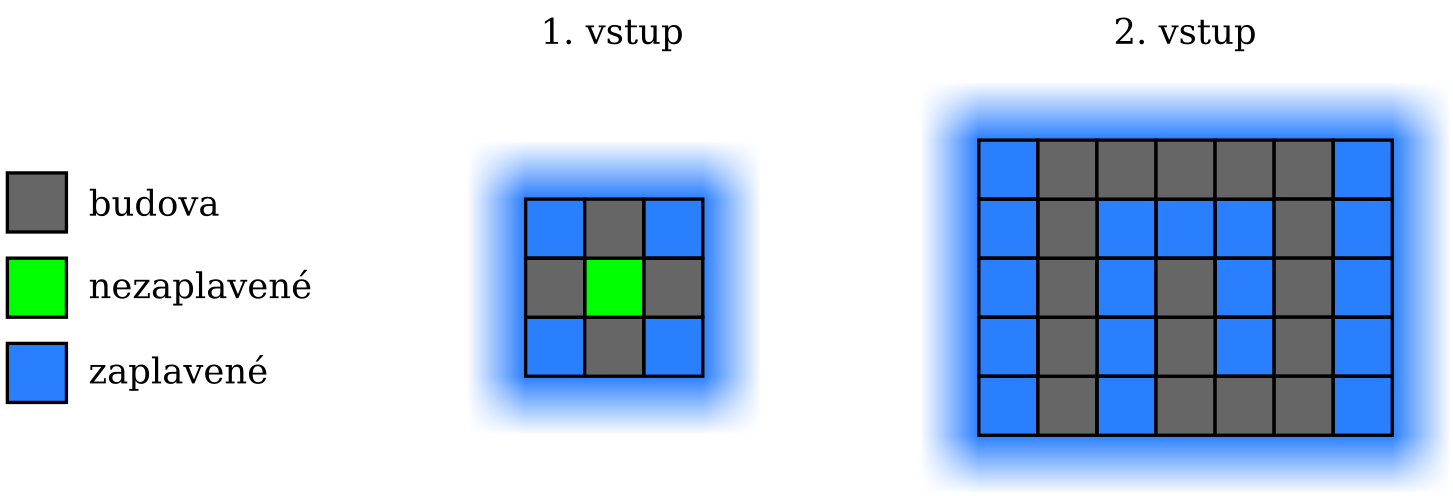
Svet si budeme predstavovať ako nekonečnú štvorcovú sieť. Nejaký obdĺžnikový kus tejto štvorcovej siete je naše mesto. Niektoré políčka v meste sú nezastavané (cesty, polia, …), na ostatných sú budovy. Každá budova zaberá presne jedno políčko. Zo všetkých strán mesta sa začne valiť voda. Voda zaplaví všetky políčka, kam sa vie dostať pohybom v 4 základných smeroch bez toho, aby prešla cez budovu. Zaujíma nás, koľko nezastavaných políčok ostane nezaplavených.
Formát vstupu
V prvom riadku vstupu sú tri celé čísla \(n, m\) a \(k\) (\(1 \leq n,m \leq 10 ^{18}\) a \(0 \leq k \leq 10^6\)): rozmery nášho mesta a počet budov v ňom.
Nasleduje \(k\) riadkov, \(i\)-ty z nich obsahuje dve celé čísla \(x_i, y_i\) – pozícu \(i\)-tej boudovy na mape. Presnejšie, \(i\)-ta budova sa nachádza v \(x_i\)-tom stĺpci a \(y_i\)-tom riadku obdĺžnika tvoriaceho naše mesto, číslujúc od \(0\). Platí teda \(0 \leq x_i < n\) a \(0 \leq y_i < m\). Možete predpokladať, že na každom políčku je najviac 1 budova.
Formát výstupu
Vypíšte jedno číslo – počet nezaplavených políčok mapy.
Hodnotenie
Pre jednotlivé sady testovacích vstupov platia nasledovné obmedzenia:
| číslo sady | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|
| \(n,m \leq\) | \(50\) | \(1\,000\) | \(1\,000\) | \(10 ^ {18}\) |
Príklady
Input:
3 3 4
2 1
0 1
1 0
1 2Output:
1Input:
7 5 17
1 0
1 1
1 2
1 3
1 4
2 0
3 0
3 2
3 3
3 4
4 0
4 4
5 0
5 1
5 2
5 3
5 4Output:
0Po zaplavení vyzerá mesto takto:
Dva semafory a štyri kruhové objazdy↩
Našou úlohou bolo pre daný plán mesta zistiť, koľko políčok ostane nezaplavených, keď sa Ipeľ vyleje. Ako už býva zvykom, pod úlohami týchto typov sa ukrýva grafové riešenie.
Prvé riešenie
Toto riešenie je založené na jednoduchej myšlienke, že pre každé políčko skúsime nájsť cestu, ktorou by ho vedel Ipeľ zaplaviť. Ak takáto cesta neexistuje, tak je dane políčko nezaplaviteľné. Ako overíme, či je nejaké políčko zaplaviteľné? Jednoducho, spustíme z neho DFS (prehľadávanie do hĺbky). Políčko je zaplaviteľné, ak sa počas DFS-ka dostaneme mimo mapu.
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
inline void magic_optimalization(){ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);}
// v programe mozeme pozuivat integery, lebo itak vyriesime iba 1.sadu
int n, m, k;
vector<vector<int>> g;
vector<vector<bool>> vis;
int xp[] = {1, -1, 0, 0}, yp[] = {0, 0, -1, 1};
bool isOk(int x, int y) {
try {
g.at(x).at(y);
return true;
} catch (const out_of_range &error) {
return false;
}
}
void clearVisited() {
vis.resize(n, vector<bool>(m));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
vis[i][j] = false;
}
}
}
bool dfs(int x, int y) {
// ak sme mimo mapy, tak sme nasli vodu
if (!isOk(x, y)) return true;
// ak sme tu boli, alebo policko je budova, vodu sme nenasli
if(vis[x][y] || g[x][y] == 1) return false;
vis[x][y] = true;
// preiterujeme susedov, ak existuje cesta mimo mapu z nejakeho
// z nich, tak existuje aj z daneho vrchola
for (int i = 0; i < 4; ++i) {
if(dfs(x+xp[i], y+yp[i])) return true;
}
return false;
}
int main() {
magic_optimalization();
cin >> n >> m >> k;
// nacitame mapu
g.resize(n, vector<int>(m));
for(int i = 0; i < k; i++) {
int x, y;
cin >> x >> y;
g[x][y] = 1;
}
// skusime z kadeho policka vyjst mimo mapu
int unflood = 0;
for (int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
if(g[i][j] == 0) {
clearVisited();
if (!dfs(i, j)) unflood++;
}
}
}
cout << unflood << endl;
return 0;
}Takéto riešenie má však zložitosť až \(O(n^2 \cdot m^2)\), pretože políčok je \(n \times m\) a DFS má v tomto prípade zložitosť \(O(n \cdot m)\). (Zamyslite sa, že ani pri použiti BFS sa časová zložitosť nezlepší.)
Vylepšenie pôvodného riešenia
Prvé riešenie nebolo zlé, bolo len príliš pomalé. Vieme ho však zrýchliť dostatočne na to, aby sme vyriešili až 3 sady vstupov (v daných sadách sa mapa zmestí do pamäte).
Treba si uvedomiť, že je dosť zbytočné robiť DFS furt z každého políčka. Ak predsa voda zaleje nejaké políčko, tak zaleje aj všetkých jeho susedov, a ich susedov… V grafovej terminologií sa tomu hovorí komponent súvislosti. Stačí mať jedno pole visited, a pre každé voľné políčko nájsť celý jeho komponent. Všetky políčka tohto komponentu si potom označíme za spracované a z nich už ďalšie prehľadávanie spúšťať nebudeme. Ak sme počas hľadania komponentu vyšli mimo mapu, vieme, že celý komponent bude nakonci zaliaty vodou.
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
inline void magic_optimalization(){ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);}
// v programe mozeme pozuivat integery, lebo poslednu sadu itak nevyriesime
int n, m, k;
vector<vector<int>> g, vis;
int xp[] = {1, -1, 0, 0}, yp[] = {0, 0, -1, 1};
bool isOk(int x, int y) {
try {
g.at(x).at(y);
return true;
} catch (const out_of_range &error) {
return false;
}
}
// zistime, ci sme pocas bfs nasli vodu a kolko policok ma dana komponenta
int foundWater, found;
void bfs(int startX, int startY) {
foundWater = found = 0;
queue<pii> q;
q.push({startX, startY});
while (q.size()) {
pii p = q.front(); q.pop();
int x = p.first, y = p.second;
// ak sme mimo mapy, tak sme nasli vodu
if (!isOk(x, y)) {
foundWater = true;
} else {
// ak sme na policku ktore je navstivene alebo budova, vratme sa na zaciatok cyklu
if(vis[x][y] || g[x][y] == 1) continue;
// inak si zaznacme, ze sme nasli nove policko, a pridajme susedne policka do radu
vis[x][y] = true;
found++;
for (int i = 0; i < 4; ++i) {
q.push({x+xp[i], y+yp[i]});
}
}
}
}
int main() {
magic_optimalization();
cin >> n >> m >> k;
// nacitajme mapu
g.resize(n, vector<int>(m));
for(int i = 0; i < k; i++) {
int x, y;
cin >> x >> y;
g[x][y] = 1;
}
// spustime bfs na kazdom volnom policku
vis.resize(n, vector<int>(m));
int unflood = 0;
for (int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
if(g[i][j] == 0 && !vis[i][j]) {
bfs(i, j);
if(!foundWater) unflood += found;
}
}
}
cout << unflood << endl;
return 0;
}Takéto pozorovanie nám vylepší zložitosť na \(O(n \cdot m)\), pretože každé políčko mapy spracujeme v DFS najviac raz.
Plný počet bodov
Na zisk plného počtu bodov sa musíme vysporiadať s tým, že mapa sa nám nezmestí celá do poľa. Tu si veľmi nepomôžeme a musíme vymyslieť niečo nové. Kľučom je pozorovanie, že budov celkom málo (\(\leq 10 ^ 6\)).
Každý riadok mesta, ktorý obsahuje nejaké budovy, si rozdelíme na intervaly voľných políčok, ktoré budú určené dvoma budovami. Napríklad, ak máme v riadku budovy na indexoch \(0, 13, 72\), tak si spravíme intervaly \([1, 12]\), \([14, 71]\). Každý interval je buď celý zaplavený, alebo celý nezaplavený. Tieto intervaly budeme brať ako vrcholy a vytvoríme si z nich graf. Dva intervaly (vrcholy) sú spojené hranou, ak sú na dvoch po sebe idúcich riadkoch a majú prienik. Pre smrteľníkov to znamená, že ak sa voda dostane do jedného vrchola, dostane sa aj do druhého.
Ak sú medzi dvoma nasledujúcimi riadkami s budovami nejaké prázdne riadky, celú túto skupinu prázdnych riadkov budeme reprezentovať jedným vrcholom, ktorý bude spojený so všetkými intervalmi z riadku nad ním a z riadku pod ním.
Okej, už to skoro máme, teraz stačí spustiť prehľadávanie zo všetkých krajných intervalov. Hmm, ale ako to spraviť tak, aby sme sa nezbláznili? Najjednoduchšie je do každého riadka pridať virtuálne budovy na pozície \(-\infty\) a \(\infty\). Tým nám na začiatku a na konci riadka vzniknú intervaly reprezentujúce kraj mapy. Z týchto intervalov a z intervalov v prvom a poslednom zastavanom riadku potom môžeme spustiť DFS, ktorým zistíme, ktoré intervaly budú zaplavené a ktoré nie.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline void magic_optimalization(){ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);}
ll n, m, k;
vector<bool> vis;
vector<vector<int>> g;
struct Node {
ll x, y1, y2;
Node(ll _x, ll _y1, ll _y2) {
x = _x;
y1 = _y1;
y2 = _y2;
}
};
bool intersects(Node n1, Node n2) {
// zmenime otvorene intervaly na zatvorene
int a1 = n1.y1 + 1, a2 = n1.y2 - 1;
int b1 = n2.y1 + 1, b2 = n2.y2 - 1;
// zistime, ci nemame nahodou neplatny interval
if (a1 > a2 || b1 > b2) return false;
// zistime ci sa intervaly prekryvaju
if (max(a1, b1) <= min(a2, b2)) return true;
return false;
}
void dfs(int start) {
stack<int> s; s.push(start); vis[start] = true;
while(s.size()) {
int u = s.top(); s.pop();
for (int v: g[u]) {
if (!vis[v]) {
s.push(v);
vis[v] = true;
}
}
}
}
int main() {
magic_optimalization();
cin >> n >> m >> k;
// nacitaj a utried zabrany a
// zisti najjuznejsiu a najsvernejsiu budovu
vector<pair<ll, ll>> blocked;
unordered_set<ll> added;
ll north_x = ULONG_MAX, south_x = -1;
for (int i = 0; i < k; ++i) {
ll x, y; cin >> x >> y;
blocked.push_back({x, y});
// pridame specialne budovy, ktore nam vytvoria vrchol od ktoreho zacneme zaplavovat
for (ll j = x-1; j <= x+1; ++j) {
if (!added.count(j)) {
blocked.push_back({j, -1});
blocked.push_back({j, m});
added.insert(j);
}
}
north_x = min(north_x, x);
south_x = max(south_x, x);
}
sort(blocked.begin(), blocked.end());
// vytvor pomocny graf
vector<Node> nodes;
int block = 0;
while (block < blocked.size()) {
ll x = blocked[block].first, y = blocked[block].second;
while (block < blocked.size() && blocked[block].first == x) {
nodes.push_back(Node(x, y, blocked[block].second));
y = blocked[block].second;
block++;
}
}
// vytvor graf
g.resize(nodes.size());
int u = 0, v = 0;
while(u < nodes.size()) {
// preiterujeme mensi alebo rovnaky riadok mapy
while (v < nodes.size() && nodes[v].x <= nodes[u].x) v++;
// zaujima iba prvy vacsi riadok a iba pokym je
// medzi prienikom danych intervalov prazdne miesto
while (v < nodes.size() && nodes[u].x + 1 == nodes[v].x) {
//cout << "T: "<< u << " " << v << endl;
if (intersects(nodes[u], nodes[v])) {
g[u].push_back(v);
g[v].push_back(u);
}
// bud zvysime v alebo zvysime u
if (nodes[u].y2 < nodes[v].y2) break;
else v++;
}
u++;
}
// spusti dfs z kadeho krajneho intervalu
vis.resize(nodes.size());
for (int i = 0; i < nodes.size(); ++i) {
if (nodes[i].x == south_x + 1 ||
nodes[i].x == north_x - 1 ||
nodes[i].y1 == -1 ||
nodes[i].y2 == m) {
dfs(i);
}
}
// spocitaj nezaplavene uzemia
ll unflood = 0;
for (int i = 0; i < nodes.size(); ++i) {
if (!vis[i]) {
// obcas sme zapocitali aj zabranu (x, x)
unflood += max(0LL, nodes[i].y2 - nodes[i].y1 - 1);
}
}
cout << unflood << endl;
return 0;
}Počet vrcholov v našom grafe (intervalov) je priamo úmerný počtu budov (nanajvýš trikrát väčší) a dá sa ukázať, že počet hrán tiež. Časová zložitosť nášho algoritmu je teda \(O(k \log k)\), keďže graf dokážeme po utriedení budov zostrojiť v lineárnom čase a DFS navštívi každý vrchol najviac raz. Pamäťová zložitosť je \(O(k)\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.