Zadanie
Mišo ukázal Zajovi, aká rýchla je jeho grafická knižnica napísaná v jazyku Go:
“Pozri, ako rýchlo vygenerujem veľa náhodných čiernych a bielych štvorcov!”, povedal Mišo a hneď sa mu na obrazovke zjavili čierne a biele štvorčeky.
“Hmm, to bolo rýchle. Ale bolo to naozaj náhodné?” začudoval sa Zajo.
“Pozri, spustím to ešte raz a bude to vyzerať inak.”, povedal Mišo a tak aj spravil. Nový obrázok vyzeral naozaj inak.
“No, niečo sa zmenilo, ale čo tie dva veľké štvorce, jeden čierny a jeden biely? Také tam boli aj minule.” poznamenal Zajo.
“No dobre, ono to nie je celkom náhodné. Najprv si rozdelím celý štvorec na štvrtiny, náhodne jednu vyfarbím na bielo, jednu na čierno a ostatné dve rekurzívne rovnako.” priznal sa Mišo.
Zajo sa na chvíľu zamyslel a opýtal sa Miša: “Ak by som ti dal čiernobiely obrázok, aký najpodobnejší obrázok by k nemu dokázal tvoj postup vygenerovať?”.
Mišo pohotovo odvetil: “Tak to teda neviem, ale myslím si, že riešitelia KSP by nám s tým vedeli pomôcť.”.
“To je pravda. Zaujímalo by ma, či to zvládnu rýchlejšie ako my postavíme snehuliaka. Pozri, koľko snehu napadlo!”, povedal Zajo a išli spolu stavať snehuliaka.
Úloha
Mišov program dokáže generovať štvorcové obrázky, ktorých šírka (a tým pádom aj výška) je mocnina dvojky. Program postupuje takto:
- Ak je strana štvorca \(1\), vyfarbi ho náhodne, buď celý na bielo, alebo celý na čierno
- Inak:
2.1. Rozdeľ štvorec na 4 menšie štvorce
2.2. Náhodnú zo 4 štvrtín vyfarbi na bielo
2.3. Náhodnú zo zvyšných troch štvrtín vyfarbi na čierno
2.4. Pre zvyšné dve štvrtiny opakuj od kroku 1.
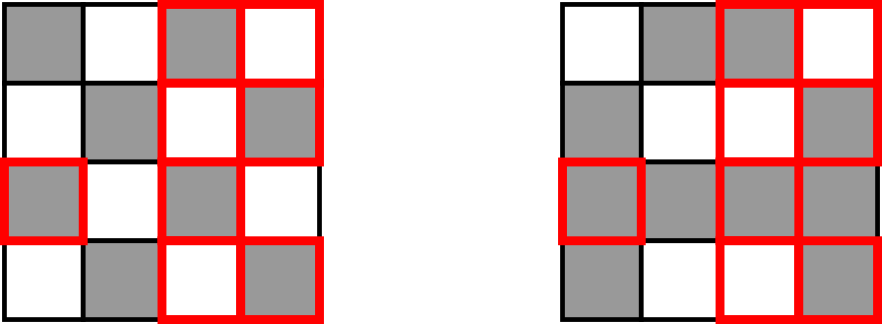
Podobnosť dvoch obrázkov definujeme ako veľkosť plochy, na ktorej majú oba obrázky rovnakú farbu. Napríklad nasledujúce dva obrázky majú podobnosť 8 (zhodujú sa v červeno orámovaných políčkach).
Na vstupe dostanete čierno-biely štvorcový obrázok. Zistite, aký najpodobnejší obrázok by dokázal Mišov postup vygenerovať (spomedzi všetkých takých, ktoré má šancu vygenerovať).
Formát vstupu
Na prvom riadku je čílo \(n\), \((1 \leq n \leq 512)\) – dĺžka strany štvorca. Číslo \(n\) je vždy mocnina čisla \(2\).
Nasleduje \(n\) riadkov po \(n\) čísel 0 alebo 1 (nie sú oddelené medzerami). Číslo 0 znamená bielu, 1 znamená čiernu farbu.
Formát výstupu
Na prvý riadok vypíšte, na koľkých miestach sa bude Mišov najpodobnejší obrázok odlišovať od toho na vstupe. Ďalej vypíšte najpodobnejší obrázok v rovnakom formáte ako obrázok na vstupe. Ak je viac možností, vypíšte ľubovolnú z nich.
Hodnotenie
Pre jednotlivé sady testovacích vstupov platia nasledovné obmedzenia:
| číslo sady | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|
| \(n \leq\) | \(8\) | \(64\) | \(256\) | \(512\) |
Príklady
Input:
4
1001
0011
0111
1111Output:
1
0001
0011
0111
1111Input:
4
1010
0101
1010
0101Output:
4
0011
0011
1010
0101Tento vstup má viacero riešení.
Mišov program si náhodne vyberá, ktorá štvrtina obrázku bude biela a ktorá čierna. Našou úlohou je zistiť, ako si má program vyberať tak, aby bol vygenerovaný obrázok čo najviac podobný obrázku na vstupe.
Môžeme si to predstaviť tak, že necháme bežať program a vždy, keď si má náhodne vybrať, podstrčíme mu to “správne” umiestnenie čierneho a bieleho štvorca. Takýmto spôsobom vieme jednoducho vytvoriť výsledný obrázok, ktorý potrebujeme vypísať na výstup. Ostáva nám zistiť, ktoré je to “správne” rozloženie štvorcov.
Ako nájsť najlepšie rozloženie?
Aby sme našli najlepšie rozloženie štvorca so stranou \(n\), potrebujeme zistiť, kam umiestniť biely a čierny štvorec. Koľko na to máme možností? Vyberáme zo štyroch štvrtín štvorca. Jedna má byť biela, jedna čierna, a ostatné dve budú vyfarbené rekurzívne, ako keby to boli samostatné obrázky so stranou \(\frac{n}{2}\) (ak sú väčšie ako 1 štvorček). Znamená to, že vyfarbíme jeden zo štyroch štvorcov na bielu a potom jeden zo zvyšných troch na čiernu, čo je spolu \(4 \cdot 3 = 12\) možností. Zvyšné dva štvorce sa vyfarbia rekurzívne.
Pre každú možnosť potrebujeme zistiť, ako veľmi by sa líšil výsledný obrázok od zadaného (ďalej skóre). Aby sme vedeli rýchlo zistiť skóre jednotlivých štvrtín, použijeme niekoľko trikov.
Pre skóre bieleho štvorca potrebujeme vedieť, koľko jednotiek sa nachádza v príslušnom štvorci na zadanom obrázku. V našom obrázku sú len nuly a jednotky, čiže počet jednotiek vo štvorci je vlastne súčet všetkých čísel vo štvorci. S tým nám pomôžu dvojrozmerné prefixové súčty. Ich výpočet nám trvá čas lineárny od veľkosti obrázku, a potom sme schopní v konštantnom čase zodpovedať otázky tvaru: “Aký je súčet čísel v tomto obdĺžniku?”
Pre čierny štvorec potrebujeme vedieť, koľko núl sa nachádza v príslušnom štvorci. Počet núl vo štvorci je počet jeho políčok mínus počet jednotiek v ňom, a obe z týchto hodnôt už vieme vypočítať.
Ostáva nám zistiť, aké skóre majú štvorce, ktoré vyplníme rekurzívne. Ak sú tieto štvorce \(1 \times 1\), skóre je vždy \(0\), lebo si môžeme zvoliť farbu. Ak sú väčšie, zistíme to rekurzívne. Použijeme teda rovnaký postup, ako keď zisťujeme skóre veľkého štvorca (vyskúšame všetkých \(12\) možností).
Toto riešenie je ale pomalé, dostali by sme za neho \(2\) body.
Prečo je to pomalé?
V prvom kroku máme \(12\) možností ktoré skúšame. Z týchto \(12\) možností je každý menší štvorec \(3\)-krát čierny, \(3\)-krát biely a \(6\)-krát určovaný rekurzívne. Rekurzívnych volaní je teda spolu \(24\).
V každom z týchto rekurzívnych volaní sa deje to isté. Na druhej úrovni už máme \(24 \cdot 24 = 576\) volaní na \(4 \cdot 4 = 16\) štvorcov, pre ktoré chceme zistiť skóre. Očividne robíme niečo zbytočne viac krát. Predídeme tomu jednoducho tak, že vždy, keď poprvýkrát zrátame skóre niektorého štvorca, si jeho skóre zapamätáme. Neskôr, keď budeme chcieť zistiť jeho skóre, sa iba pozrieme na zapamätanú hodnotu. Aký dopad bude mať táto malá zmena? Pozrime sa napríklad opäť na druhú úroveň. Budeme na nej mať už len \(16\) rekurzívnych volaní, a zvyšných \(576 - 16 = 560\) volaní už vyhodnotíme v konstantnom čase tak, že sa pozrieme na zapamätanú hodnotu.
Tento postup sa volá memoizácia. Ďalšiu ukážku použitia memoizácie nájdete napríklad v úlohe Optimálna šifrovačka.
Časová zložitosť
Pri úlohách, v ktorých je vstup dvojrozmerný (tabuľka, mriežka), máme dve možnosti, ako zapísať časovú zložitosť. Buď ju môžeme uvádzať zložitosť od skutočného počtu čísel na vstupe (veľkosti vstupu) alebo od dĺžky strany štvorca. My budeme uvádzať zložitosť v závislosti od čísla \(N = n \cdot n\), teda od veľkosti vstupu.
Na začiatku si predrátame prefixové súčty obrázku na vstupe, pomocou ktorých neskôr budeme zisťovať skóre bielych a čiernych štvorcov v konštantnom čase. Na to potrebujeme \(O(N)\) času. Zaujímavejšie je to s našou rekurzívnou funkciou.
Vďaka memoizácii sa rekurzívne volanie pre každý štvorec vykoná iba raz. Pri každom ďalšom volaní len vráti už uložené riešenie. Počet volaní tejto funkcie je teda rovnaký, ako počet rôznych štvorcov, na ktoré sa funkcia zavolá.
Na začiatku máme štvorec veľkosti \(N\). V ďalšom kroku máme \(4\) štvorce veľkosti \(\frac{N}{4}\), potom \(16\) štvorcov veľkosti \(\frac{N}{16}\), a tak ďalej až po \(N\) štvorcov s veľkosťou \(1\). Dostávame postupnosť \(1 + 4 + 16 + 64 + ... + N\) štvorcov všetkých veľkostí.
Aby sme ukázali, že súčet tejto postupnosti je \(O(N)\), porovnáme ju s postupnosťou \(1+2+4+8+...+N = 2N-1\). Vidíme, že naša postupnosť obsahuje len niektoré jej členy a teda náš súčet bude určite menší. Z toho vyplýva, že celkový počet štvorcov, a teda aj počet volaní funkcie, je \(O(N)\).
Teraz potrebujeme ešte zistiť, ako dlho trvá výpočet jedného volania. Potom to vynásobíme počtom volaní a dostaneme zložitosť celého výpočtu. Aby sme zistili zložitosť iba jedného volania, budeme predpokladať, že všetky volania, ktoré bude potrebovať, sú už vyrátané.
Čo robí jedno volanie? Zisťujeme v ňom skóre menších štvorcov a podľa nich vyberieme najlepšie z \(12\) možných rozložení. Zisťovanie skóre pre biely a čierny štvorec je vďaka prefixovým súčtom v \(O(1)\), skóre ostatných štvorcov zistíme opätovným volaním našej funkcie, čo môžeme kvôli rekurzii považovať za \(O(1)\).
Spolu bude teda výpočet celého rozloženia trvať \(O(N) \cdot O(1) = O(N)\).
Na koniec nám ostáva len skonštruovať obrázok na výstup. Na to stačí priamočiara simulácia Mišovho programu (keď už vieme, ktoré štvorce majú byť biele a ktoré čierne). Pri takejto simulácii iba vypĺňame tabuľku veľkosti \(N\), na čo potrebujeme opäť \(O(N)\) času.
Celková časová zložitosť je teda \(O(N)\). Pamäťová tiež, lebo si pamätáme obrázok veľkosti \(O(N)\) a skóre už vyrátaných štvorcov, ktorých je \(O(N)\).
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
vector<string> zadanie;
vector<string> riesenie;
vector<vector<int>> prefix_sum;
// memoizácia, indexujeme stredom štvorca
vector<vector<int> > mem; //najlepšie skóre pre štvorec
vector<vector<array<int, 2>>> memk; //ako sme dostali najlepšie skóre
int dx[] = {0, 0, 1, 1}; //tieto polia nám neskôr ušetria veľa podmienok
int dy[] = {0, 1, 0, 1};
int diff_zeros(int a, int b, int c, int d){
return prefix_sum[c][d] + prefix_sum[a][b] - prefix_sum[a][d] - prefix_sum[c][b];
}
int diff_ones(int a, int b, int c, int d){
return (c - a) * (d - b) - (prefix_sum[c][d] + prefix_sum[a][b] - prefix_sum[a][d] - prefix_sum[c][b]);
}
//hladá najlepšie rozloženie
int diff(int a, int b, int c, int d){
if(c - a == 1)
return 0;
int sx = a + (c - a) / 2 - 1,
sy = b + (d - b) / 2 - 1;
if(mem[sx][sy] != -1) //výsledok pre tento štvorec už máme zrátaný
return mem[sx][sy];
else{
int l = (c - a) / 2; //strana menšieho štvorca
int m = c * d; //najlepšie skóre pre tento štvorec
array<int, 2> k; //ako dostaneme najlepšie skóre
//vyskúšame 12 možností
for(int x = 0; x < 4; x++){
for(int y = 0; y < 4; y++){
if(x == y) continue;
int t = diff_zeros(a + dx[x] * l, b + dy[x] * l, c - (1 - dx[x]) * l, d - (1 - dy[x]) * l) +
diff_ones(a + dx[y] * l, b + dy[y] * l, c - (1 - dx[y]) * l, d - (1 - dy[y]) * l);
for(int z = 0; z < 4; z++){
if(x == z || y == z) continue;
t += diff(a + dx[z] * l, b + dy[z] * l, c - (1 - dx[z]) * l, d - (1 - dy[z]) * l);
}
if(t < m){
m = t;
k = {x, y};
}
}
}
mem[sx][sy] = m;
memk[sx][sy] = k;
return m;
}
}
void fill_zeros(int a, int b, int c, int d){
for(int i = a; i < c; i++)
for(int j = b; j < d; j++)
riesenie[i][j] = '0';
}
void fill_ones(int a, int b, int c, int d){
for(int i = a; i < c; i++)
for(int j = b; j < d; j++)
riesenie[i][j] = '1';
}
//konštruuje výsledok z predrátaného rozloženia memk
void fill(int a, int b, int c, int d){
if(c - a > 1){
int sx = a + (c - a) / 2 - 1,
sy = b + (d - b) / 2 - 1;
array<int, 2> kde = memk[sx][sy];
int x = kde[0], y = kde[1];
int l = (c - a) / 2;
fill_zeros(a + dx[x] * l, b + dy[x] * l, c - (1 - dx[x]) * l, d - (1 - dy[x]) * l);
fill_ones(a + dx[y] * l, b + dy[y] * l, c - (1 - dx[y]) * l, d - (1 - dy[y]) * l);
for(int z = 0; z < 4; z++){
if(x == z || y == z) continue;
fill(a + dx[z] * l, b + dy[z] * l, c - (1 - dx[z]) * l, d - (1 - dy[z]) * l);
}
}
}
int main(){
int n;
cin >> n;
zadanie.resize(n);
riesenie.resize(n);
prefix_sum.resize(n + 1);
prefix_sum[0].resize(n + 1, 0);
for(int i = 1; i <= n; i++){
prefix_sum[i].resize(n + 1);
prefix_sum[i][0] = 0;
cin >> zadanie[i - 1];
riesenie[i - 1] = zadanie[i - 1];
for(int j = 1; j <=n; j++){
prefix_sum[i][j] = prefix_sum[i - 1][j] + prefix_sum[i][j - 1] -
prefix_sum[i - 1][j - 1] + zadanie[i - 1][j - 1] - '0';
}
}
mem.resize(n, vector<int>(n, -1));
memk.resize(n, vector<array<int, 2>>(n));
int ans = diff(0, 0, n, n);
fill(0, 0, n, n);
cout << ans << endl;
for(int i = 0; i < n; i++){
cout << riesenie[i] << endl;
}
}
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.