3. Korman je gurmán vzorové riešenie

Zadanie

Máme tu ďalší problém. Andrej má narodeniny a k nim dostal veľký počet darčekov. Keďže si vždy na narodeniny prial len a len veľkú sladkú čokoládu a mamka už nemohla počúvať to jeho večné fňukanie, tak sa rozhodla, že mu kúpi tú najväčšiu, akú v meste majú.

Mamka si myslela, že čokoláda všetko vyrieši a bude pokoj. Ale nevyriešila. Andrej je gurmán a jeho gurmánske požiadavky sú známe už v ďalekej Číne, možno aj ďalej. Andrej jednoducho nemôže zjesť čokoládu ako normálny človek. On si čokoládu rozdelil na kocky, kde každá kocka má svoju sladkosť. Tieto kocky následne uložil do jedného dlhého radu na stole.

Andrej chce teraz zjesť všetky kocky zaradom zľava doprava. Pritom chce, aby každá ďalšia kocka, ktorú zje, bola sladšia alebo rovnako sladká ako predchádzajúca. Andrej je ešte k tomu veľmi lenivý a jediné, čo vie spraviť, je zobrať nejakú kocku čokolády a dať ju na začiatok radu. S touto požiadavkou šiel k mamke, aby mu povedala, koľko preložení treba urobiť, aby boli kocky usporiadané. Lenže mamka ho už má plné zuby a keďže nevedela čo spraviť, zavolala na linku prvej pomoci KSP a žiadá vás o pomoc.

Úloha

Na vstupe máte číslo \(n\) a pole čísel veľkosti \(n\). Vašou úlohou je vypočitať, koľko najmenej operácií je potrebných na usporiadanie poľa od najmenšieho čísla po najvačšie. Jediná operácia, ktorú máte povolenú, je zobrať nejaké čislo v poli a preložiť ho na začiatok. Zaujíma nás len počet týchto preložení.

Formát vstupu

Na prvom riadku vstupu sa nachádza celé číslo \(n\) (\(1 \leq n \leq 1\,000\,000\)) – počet kociek čokolády. Na druhom riadku sa nachádza \(n\) čísel \(s_1, s_2, \dots s_n\), kde \(s_i\) označuje sladkosť \(i\)-tej kocky. Pre každé \(i\) platí \(0 \leq s_i \leq 10^9\).

Vaše riešenie otestujeme na štyroch testovacích sadách. V prvých dvoch sadách máte zaručené, že na vstupe sa budú vždy nachádzať čísla od \(1\) po \(n\), každé práve raz. Za riešenie, ktoré vyrieši takúto podúlohu, viete získať až polovicu bodov.

Formát výstupu

Na jediný riadok výstupu vypíšte najmenší možný počet preložení potrebných na to, aby boli kocky usporiadané od najmenej sladkej po najsladšiu. Výstup ukončite znakom nového riadku.

Príklady

Input:

5
5 1 2 3 4

Output:

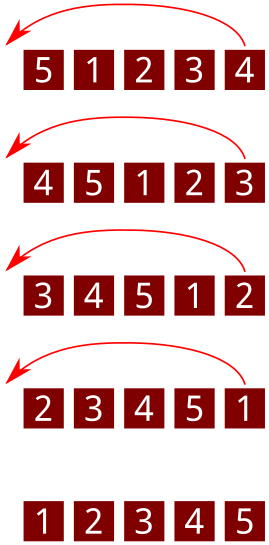
4

Najprv preložíme na začiatok kocku so sladkosťou 4. Potom kocku so sladkosťou 3, potom 2, a nakoniec 1. Urobili sme 4 preloženia.

Input:

6
1 1 1 1 1 1

Output:

0

V tomto prípade netreba prekladať nič.

Input:

10 
1 5 6 50 12 3 499 5000001 3 3

Output:

7

Našou úlohou je usporiadať pole čísel od najmenšieho po najväčšie len pomocou toho, že budeme čísla prenášať na začiatok poľa. Presnejšie povedané, chceme zistiť, na koľko najmenej takýchto operácií sa dá naše pole usporiadať.

V tomto vzoráku si v prvej časti predstavíme základné pozorovania potrebné pre vyriešenie tejto úlohy – popisy vašich riešení by mohli obsahovať aspoň hrubo zvýraznené myšlienky. V druhej časti si ukážeme, ako sa dá jednoducho vypočítať riešenie v čase \(O(n)\), ak vstup obsahuje len čísla \(1\) až \(n\) a ako sa dá toto riešenie zovšeobecniť pomocou triedenia na ľubovolné pole a dostať riešenie v čase \(O(n \log n)\). Ak vás zaujíma len optimálne riešenie, môžete po prečítaní prvej časti preskočiť na poslednú časť, kde si ukážeme, ako získať časovú zložitosť \(O(n)\) pomocou zásobníka.

Myšlienka riešenia

Prvé pozorovanie, ktoré nám pomôže pri riešení, je, že každé pole dĺžky \(n\) vieme usporiadať s použitím \(n\) operácií. Najprv presunieme na začiatok najväčšie číslo, potom druhé najväčšie, potom tretie, atď. Na konci postupu tak preložíme na začiatok najmenšie číslo a dostaneme usporiadané pole.

Pri takomto postupe ale robíme niektoré operácie zbytočne. Môžeme si všimnúť, že najväčšie číslo nikdy prekladať nemusíme. Ak totiž preložíme ostatných \(n - 1\) čísel, najväčšie číslo bude na konci poľa – teda tam, kde má byť.

Podobne si môžeme všimnúť, že ak je druhé najväčšie číslo naľavo od najväčšieho, ani toto číslo presúvať nemusíme, lebo keď vykonáme zvyšných \(n - 2\) operácií (presunieme na začiatok tretie najväčšie, štvrté najväčšie, …, najmenšie) tak bude pole usporiadané. Túto úvahu môžeme zovšeobecniť.

Predpokladajme, že \(k\) najväčších čísel je na vstupe v správnom poradí (\(k\)-te najväčšie je naľavo od \((k-1)\)-vého najväčšieho, to je naľavo od \((k-2)\)-hého, …). Potom nám stačí postupne presunúť zvyšných \(n-k\) čísel, teda urobíme \(n-k\) operácií.

Ak je naše \(k\) najväčšie možné (teda \((k+1)\)-vé najväčšie číslo je už napravo od \(k\)-teho), tak sa pole nedá utriediť na menej ako \(n-k\) operácií. Niekedy totiž musíme presunúť \((k+1)\)-vé najväčšie číslo, aby sme ho dostali naľavo od \(k\)-teho. A potom budeme už musieť preložiť aj všetky menšie čísla aby sme ich dostali pred neho. To znamená, že každé z \(n-k\) najmenších čísel musíme aspoň raz presunúť.

Zoberme si ako príklad postupnosť: \(5, 6, 3, 7, 2, 1, 4\). Tri najväčšie čísla sú v správnom poradí (\(5\) je naľavo od \(6\) a \(6\) od \(7\)), teda najväčšie možné \(k\) je \(3\). Číslo \(4\) niekedy určite presunúť musíme, aby sme ho dostali naľavo od \(5\). Potom musíme na začiatok popresúvať aj všetky menšie čísla: \(3, 2, 1\).

Na vyriešenie úlohy nám teda stačí nájsť najväčšie také \(k\), že \(k\) najväčších čísel je na vstupe v správnom poradí, a potom vypísať hodnotu \(n - k\). Otázkou stále zostáva, ako zistiť hodnotu \(k\).

Riešenie pre čísla \(1\) až \(n\)

V polovici vstupných sád platilo, že na vstupe sa nachádza \(n\)-prvkové pole čísel \(1\) až \(n\). Pri takýchto vstupoch vieme hneď povedať, že najväčšie číslo bude \(n\), druhé najväčšie \(n-1\), atď.

Mohli by sme teda pre každé číslo od \(n\) po \(1\) zisťovať, či sa naľavo od neho nenachádza väčšie číslo, čím by sme dostali algoritmus s časovou zložitosťou \(O(n^2)\).

Efektívnejšie však bude priamo zostrojiť postupnosť \(k\) najväčších čísel. Pole raz prejdeme sprava doľava a postupne budeme hľadať čísla od najväčšieho po najmenšie. Aktuálne hľadané číslo si označíme ako hladane_cislo. Najprv hľadáme číslo \(n\). Vždy keď nájdeme hladane_cislo, ďalej hľadáme najväčšie menšie číslo, teda hladane_cislo zmenšíme o \(1\). Takto pokračujeme až kým neprídeme na začiatok poľa. Popritom si počítame, koľkokrát sme našli a zmenšovali hladane_cislo – tento počet je naše hľadané \(k\).

Takéto riešenie má časovú aj pamäťovú zložitosť \(O(n)\), lebo len raz prejdeme celé pole a v pamäti držíme len jedno pole dĺžky \(n\) a zopár jednoduchých premenných.

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n;
    cin >> n;
    vector<int> pole(n);
    for(int i=0; i<n; i++) {
        cin >> pole[i];
    }
    
    int k = 0, hladane_cislo = n;

    for(int i=n-1; i>=0; i--) {
        if(pole[i] == hladane_cislo) {
            hladane_cislo--;
            k++;
        }
    }

    cout << n - k << endl;
    return 0;
}

Využitie tej istej myšlienky pre pole ľubovoľných čísel

Predošle riešenie fungovalo len ak pole malo čísla od \(1\) po \(n\), lebo sme predpokladali, že maximum je \(n\), druhé najväčšie číslo je \(n - 1\) atď. Ak máme v poli ľubovoľné čísla, nevieme, ktoré je najväčšie, druhé najväčšie atď.

Riešenie pre čísla od \(1\) po \(n\) však vieme jednoducho upraviť. Trik spočíva v tom, že si vytvoríme ešte jedno pole, nakopírujeme doň čísla zo vstupu a usporiadame ho vzostupne. Ak veľmi nepoznáte triediace algoritmy, odporúčame prečítať si o nich v kuchárke a v odkazoch z nej. Pri riešení tejto úlohy nám bude stačiť vedieť, že pole \(n\) prvkov vieme efektívne usporiadať v čase \(O(n \log n)\).

Pomocou usporiadaného poľa už vieme rýchlo zisťovať, aké je \(i\)-te najväčie číslo – maximum je na indexe \(n-1\) (ak pole indexujeme od 0), druhé najväčšie na indexe \(n-2\), atď. Vieme teda použiť rovnaký algoritmus ako v predošlom riešení s jednou drobnou zmenou: prezeraný prvok poľa neporovnávame s hodnotou v premennej hladane_cislo ale s prvkom utriedeného poľa s indexom index_hladaneho_cisla. V riešení teda znova prechádzame vstupné pole od konca a ak je prezerané číslo práve to hľadané, zmenšíme ukazovateľ index_hladaneho_cisla o \(1\).

Optimálne triedenie má časovú zložitosť \(O(n\log n)\), a po utriedení vykonávame len algoritmus z predošlej časti, ktorý beží v lineárnom čase \(O(n)\). Celkovo je teda časová zložitosť \(O(n\log n + n) = O(n \log n)\). Pamäťová zložitosť je \(O(n)\), lebo potrebujeme 2 polia dĺžky \(n\).

n = int(input())
A = [int(x) for x in input().split()]

B = sorted(A)

index_hladaneho_cisla = n-1
k = 0

# do `a` si postupne priradzujme prvky pola a prechadzame pole od konca
for a in A[::-1]:
    if a == B[index_hladaneho_cisla]:
        index_hladaneho_cisla -= 1
        k += 1

print(n - k)

Optimálne riešenie

Keďže pri riešení úlohy musíme minimálne prečítať celý vstup, žiadne riešenie nemôže byť rýchlejšie ako \(O(n)\). Ak teda vymyslíme algoritmus s lineárnou zložitosťou, budeme si istí, že je najlepší možný (ak porovnávame algoritmy asymptotickou časovou zložitosťou).

Predošlé riešenie nám spomaľovalo triedenie, ktoré sme potrebovali na to, aby sme vedeli určiť hľadané \(i\)-te najväčšie číslo. Ak mierime na zložitosť \(O(n)\), musíme sa triedeniu vyhnúť a ideálne vyriešiť úlohu len jedným prechodom cez pole.

Vráťme sa v úvahách späť k myšlienke “niekde v poli bude usporiadaná podpostupnosť niekoľkých najväčších čísel a práve tieto čísla nemusíme presúvať”. V predošlých riešeniach sme najprv zistili, ktoré sú to tie najväčšie čísla a potom sme konkrétnu postupnosť odzadu hľadali vo vstupnom poli. Pokúsme sa teraz začať prechádzať pole od konca, bez toho, aby sme vedeli čo hľadáme. Priebežne si budeme udržovať kandidátsku podpostupnosť – postupnosť najväčších doteraz videných čísel, ktoré boli vzájomne dobre usporiadané. Na uchovávanie kandidátskej podpostupnosti použijeme zásobník.

Vstupné pole budeme prechádzať sprava doľava, a postupne si budeme čísla vkladať do zásobníka. Predtým, než vložíme nové číslo \(x\) do zásobníka, z jeho vrchu postupne odstránime všetky čísla, ktoré sú menšie ako \(x\). To nám zabezpečí, že v zásobníku budú čísla usporiadané – na spodku bude najväčšie doteraz videné číslo. Keď prejdeme celé pole, tak na spodku bude najväčšie číslo. Druhý prvok odspodu bude najväčšie číslo, ktoré bolo naľavo od maxima. Tretí prvok odspodu bude najväčšie číslo, ktoré bolo ešte viac naľavo, atď.

Zásobník teda bude obsahovať niekoľko najväčších, dobre usporiadaných čísel, no môže obsahovať aj čísla, ktoré musíme presúvať. Pozrime sa na príklad \(1, 5, 3, 7, 2, 6, 8, 4\). Po prejdení celého poľa ostane v zásobníku podpostupnosť \(1, 5, 7, 8\). Číslo \(6\) ale musíme pri usporiadavaní preložiť na začiatok a tak budeme musieť preložiť aj \(5\) a \(1\), ktoré zostali v zásobníku. Na to, aby sme dostali našu žiadanú postupnosť nehybných čísel, musíme teda zo zásobníka odstrániť všetky čísla, ktoré sú menšie ako najväčšie odstránené číslo.

Môžeme si všimnúť, že čísla odstránené zo zásobníka počas prechodu poľa sú vlastne tie čísla, ktoré bolo nutné presunúť, lebo naľavo od nich sa nachádzalo nejaké väčšie číslo. Čísla odstránené zo zásobníka na záver sú tie čísla, ktoré bolo nutné presunúť, lebo sa pred nich dostalo nejaké väčšie číslo.

Celkový počet potrebných presunov je teda počet čísel odstránených zo zásobníka, alebo jednoducho \(n\) mínus počet čísel v zásobníku.

Toto riešenie bude mať časovú zložitosť \(O(n)\), lebo prechádzame celé pole len raz a každé číslo do zásobníka vložíme práve raz a odstránime ho najviac raz. Pamäťová zložitosť zostáva \(O(n)\), keďže potrebujeme len pole dĺžky \(n\) a zásobník dĺžky najviac \(n\). Za toto riešenie ste mohli dostať plný počet bodov.

#include <iostream>
#include <algorithm>
#include <stack>
#include <vector>

using namespace std;

int main() {
    int n;
    cin>>n;
    vector<int> pole(n);
    for(int i=0; i<n; i++) {
      cin >> pole[i];
    }
    
    int vyhodene_maximum = -1;
    stack<int> zasobnik;

    for(int i=n-1; i>=0; i--) {
        while ((!zasobnik.empty()) && (zasobnik.top() < pole[i])){
            vyhodene_maximum = max(vyhodene_maximum, zasobnik.top());
            zasobnik.pop();
        }
        zasobnik.push(pole[i]);
    }
    
    while ((!zasobnik.empty()) && (zasobnik.top() < vyhodene_maximum)) {
        zasobnik.pop();
    }
    cout << n - zasobnik.size() <<endl;
    return 0;
}