8. Automat vzorové riešenie

Zadanie

V Erikovej škole majú automat na čokoládové tyčinky. Taký klasický automat: vhodíte peniaze, vyberiete si, akú tyčinku chcete, a automat vám ju vydá.

Nedávno sa však automat pokazil, takže väčšinou vám okrem tyčinky, ktorú ste si vybrali, vysype aj nejaké ďalšie. Erik, súc charakterný mladý muž, túto poruchu ihneď nahlásil a prestal automat používať. Keďže je však Erik zároveň aj od prírody veľmi zvedavý, napadla mu jedna hypotetická otázka: koľko by toho dokázal z automatu vytiahnuť za peniaze, ktoré má práve pri sebe?

Úloha

Automat predáva \(n\) rôznych druhov tyčiniek, očíslovaných \(1\) až \(n\). Z každého druhu je v automate niekoľko kusov a každý druh má nejakú cenu (rôzne druhy môžu mať rôzne ceny). Ak si v automate kúpite tyčinku druhu \(x\), automat vám navyše vydá po jednej tyčinke z druhov \(1, 2, \dots, x-1\) (ak ešte nejaké má. Ak z nejakého druhu už nemá žiadnu tyčinku, jednoducho vám z tohto druhu nevydá nič). Ak automatu dôjdu tyčinky nejakého druhu, prestane tento druh predávať (takže tyčinky tohto druhu sa už nedajú kúpiť).

Erik má momentálne pri sebe \(k\) centov. Aká je najväčšia možná celková hodnota tyčiniek, ktoré Erik dokáže ,,kúpiť’’ z automatu za peniaze, ktoré má?

Formát vstupu

V prvom riadku vstupu sú dve medzerou oddelené celé čísla \(n, k\) (\(1 \leq n \leq 50\), \(1 \leq k \leq 200\,000\)) – počet druhov tyčiniek a množstvo peňazí, ktoré má Erik k dispozícii.

Druhý riadok obsahuje \(n\) medzerami oddelených celých čísel \(c_1, c_2, \dots, c_n\) (\(1 \leq c_i \leq 50\)), kde \(c_i\) je cena \(i\)-teho druhu tyčiniek.

Tretí riadok obsahuje \(n\) medzerami oddelených celých čísel \(p_1, p_2, \dots, p_n\) (\(0 \leq p_i \leq 50\)), kde \(p_i\) je počiatočný počet tyčiniek \(i\)-teho druhu.

Formát výstupu

Vypíšte jeden riadok obsahujúci jedno celé číslo: najväčšiu možnú hodnotu tyčiniek, ktoré dokáže Erik získať s peniazmi, ktoré má.

Príklady

Input:

5 30
15 25 10 50 5
3 6 3 5 2

Output:

285

Erik najprv za 20 centov kúpi dve tyčinky 3. druhu (pričom mu z automatu vypadnú aj po dve tyčinky 1. a 2. druhu). Následne kúpi dve tyčinky 5. druhu. Pri nákupe prvej z nich dostane aj po jednej tyčinke z prvých štyroch druhov, pri nákupe druhej z nich dostane tyčinku 2. a 4. druhu (tyčinky 1. a 3. druhu sa už minuli). Nakoniec má teda Erik 3 tyčinky 1. druhu, 4 tyčinky 2. druhu, 3 tyčinky 3. druhu, a po 2 tyčinky 4. a 5. druhu.

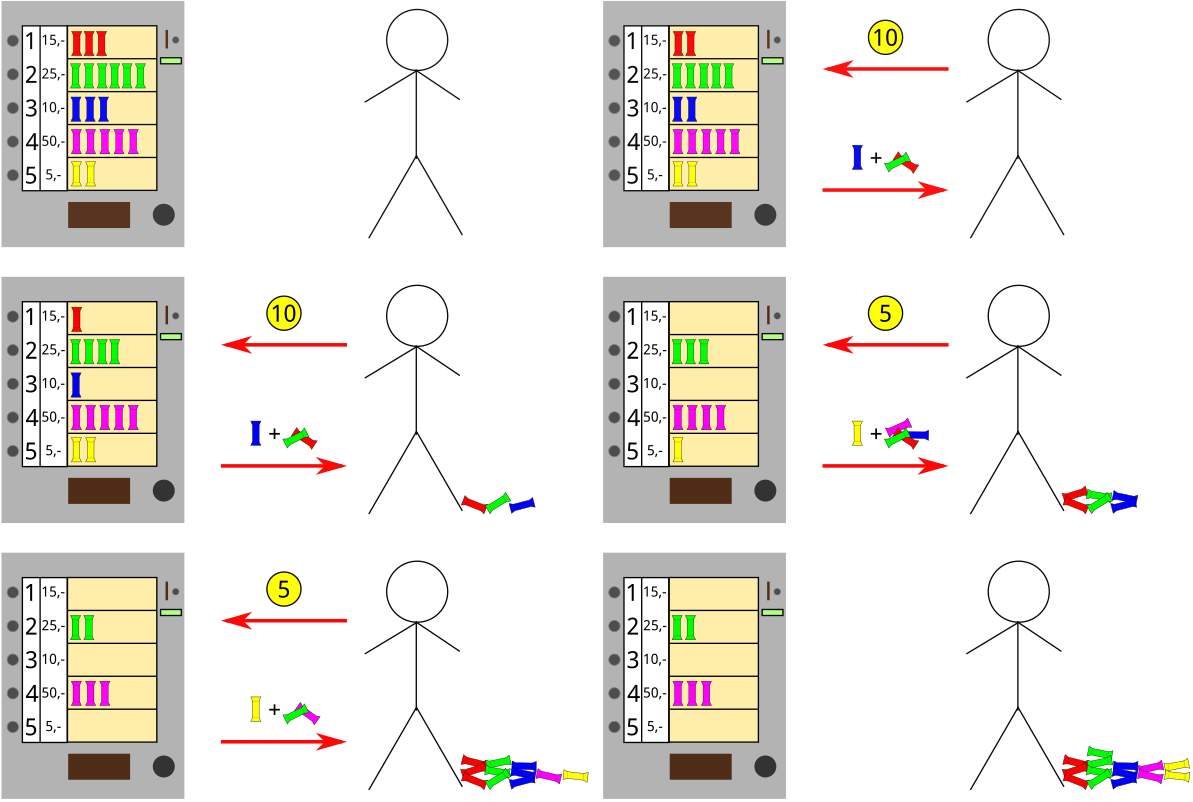
Spôsobov, ako môže Erik postupne nakupovať tyčinky, je veľa. Na začiatok je preto dobré uvedomiť si, že je dôležité, koľko akých tyčiniek Erik kúpi, ale nie je dôležité, v akom poradí:

• Ak nám Erik povie, že kúpil (t. j. vybral a zaplatil) \(t_1, t_2, \dots, t_n\) tyčiniek druhov \(1, 2, \dots, n\), vieme už jednoznačne určiť, koľko akých tyčiniek mu automat vysypal:

  • Tyčinky druhu \(n\) dával automat Erikovi iba vtedy, keď si ich naozaj kúpil, teda Erik ich dostal dokopy \(t_n\).

  • Tyčinky druhu \(n-1\) sa automat snažil Erikovi dať vždy, keď si kúpil tyčinku druhu \(n-1\) alebo \(n\). To znamená, že ak má automat na začiatku \(t_n + t_{n-1}\) alebo viac tyčiniek druhu \(n-1\), Erik bude mať na konci \(t_n + t_{n-1}\) tyčiniek tohto druhu. V opačnom prípade dostane Erik všetkých \(p_{n-1}\) tyčiniek druhu \(n-1\).

  • Túto úvahu môžeme zovšeobecniť: tyčiniek druhu \(i\) Erik dostane presne \[\min(p_i,\,\, t_i + t_{i+1} + \dots + t_n) \text{.}\]

Samozrejme, ak by Erik nakupoval tyčinky v zlom poradí, mohol by sa nejaký druh minúť skôr, než z neho Erik kúpi všetky tyčinky ktoré chcel. Tomuto sa však vždy dá ľahko vyhnúť: jednoducho najprv nakúpime všetky tyčinky druhu \(1\) ktoré chceme, potom tyčinky druhu \(2\), potom druhu \(3\) atď.. Ako sme si ukázali, toto poradie je rovnako dobré ako každé iné.

Pri hľadaní optimálneho riešenia teda môžeme spokojne zabudnúť na to, že tyčinky sa kupujú v nejakom poradí a stačí nám nájsť optimálnu sadu tyčiniek, ktoré má Erik kúpiť.

Dynamické programovanie

Naše riešenie bude založené na technike zvanej dynamické programovanie. Keď riešime úlohu pomocou dynamického programovania, musíme si položiť dobrú otázku. V našom prípade to bude otázka:

Pre dané \(X, Y, Z\): Akú najväčšiu hodnotu vieme získať v tyčinkách prvých \(X\) druhov, ak na tyčinky prvých \(X\) druhov minieme nanajvýš \(Y\) peňazí a z posledných \(n-X\) druhov kúpime dokopy presne \(Z\) tyčiniek?

Táto otázka znie dosť krkolomne,¹ má však niekoľko kľúčových dobrých vlastností. Označme si odpoveď na našu otázku pre nejaké \(X, Y, Z\) ako \(o(X, Y, Z)\):

• Je len ohraničený počet možných trojíc \(X, Y, Z\), pre ktoré má zmysel sa našu otázku pýtať.
• Hodnota \(o(n, k, 0)\) je riešením našej úlohy.
• Ak \(X = 0\), odpoveď vieme ľahko zistiť: je rovná \(0\).

• Odpoveď pre nejaké \(X > 0, Y, Z\) vieme ľahko zistiť, ak poznáme odpovede pre menšie \(X\). Stačí nám rozobrať všetky možnosti, koľko tyčiniek druhu \(X\) kúpime:

  • Ak sa rozhodneme nekúpiť žiadnu tyčinku druhu \(X\), získame od automatu \(\min(Z, p_X)\) tyčiniek tohto druhu (keďže kupujeme \(Z\) tyčiniek druhov s vyšším číslom). Tie budú mať hodnotu \(c_X \cdot \min(Z, p_X)\). V tyčinkách druhov \(1\) až \(X-1\) potom získame nanajvýš \(o(X-1, Y, Z)\) peňazí, dokopy teda získame \(c_X \cdot \min(Z, p_X) + o(X-1, Y, Z)\).
  • Ak kúpime jednu tyčinku druhu \(X\), získame \(\min(Z+1, p_X)\) tyčiniek druhu \(X\), v hodnote \(c_X \cdot \min(Z+1, p_X)\). Na tyčinky druhov \(1\) až \(X-1\) nám pritom ostane \(Y - c_X\) peňazí, pričom tyčiniek druhov \(X\) až \(n\) kupujeme dokopy \(Z+1\). To znamená, že v tyčinkách druhov \(1, \dots, X-1\) získame nanajvýš \(o(X-1, Y-c_X, Z+1)\) peňazí, dokopy \(o(X-1, Y-c_X, Z+1) + c_X \cdot \min(Z+1, p_X)\).
  • Všeobecne, ak kúpime \(k\) tyčiniek druhu \(X\), získame \(c_X \cdot \min(Z+k, p_X)\) v tyčinkách druhu \(X\) a \(o(X-1, Y-k c_X, Z+k)\) v tyčinkách nižších druhov. Toto má, samozrejme, zmysel iba pre také \(k\), že \(k c_X \leq Y\) a \(k \leq p_X\).

  Hodnota \(o(X, Y, Z)\) je teda maximum z hodnôt \[c_X \min(Z+k, p_X) + o(X-1, Y-k c_X, Z+k)\] pre všetky zmysluplné \(k\).

Odpoveď na našu otázku by sme teda vedeli počítať jednoduchou rekurzívnou funkciou:

function o(X, Y, Z):
    if X = 0:
        return 0
    best := 0
    max_k := min(Y / c[X], p[X])
    for k := 0, 1, ... , max_k:
        best := max(best, c[X] * min(Z + k, p[X]) + o(X-1, Y - k * c[X], Z + k))
    return best

Túto funkciu nám stačí zavolať pre \(X = n, Y = k, Z = 0\) a ona nám vypočíta výsledok. Keďže v rekurzívnych volaniach sa táto funkcia volá so stále menším \(X\) (a pre \(X = 0\) sa už rekurzívne nevolá), skončí to v konečnom čase. Časová zložitosť však bude nepekná.

Memoizácia

Časovú zložitosť nášho algoritmu môžeme podstatne zlepšiť tým, že prestaneme počítať rovnaké veci veľakrát. Konkrétne, vždy keď zavoláme našu funkciu pre nejakú kombináciu \(X, Y, Z\) prvý raz, spočítame výsledok a zapamätáme si ho. Keď niekedy neskôr zavoláme funkciu s tými istými parametrami, nebudeme ju znovu počítať, ale vrátime už zapamätaný výsledok. Tomuto triku sa hovorí memoizácia. Uvedomte si, že tým preskočíme aj rekurzívne volania, ktoré by vyprodukovali kopec ďalších rekurzívnych volaní, takže nám to často ušetrí veľmi veľa času.

Ako si však pamätať vypočítané hodnoty našej funkcie? Jednoducho: použijeme obyčajné trojrozmerné pole, kde na indexe [X][Y][Z] bude buď hodnota \(o(X, Y, Z)\) ak sme ju už niekedy spočítali, alebo špeciálna hodnota (napr. -1, NULL alebo None) signalizujúca, že sme \(o(X, Y, Z)\) ešte nikdy nepočítali.

Aké veľké má byť toto pole? Parameter \(X\) bude v každom volaní funkcie o(X, Y, Z) niekde medzi \(0\) a \(n\). Parameter \(Y\) bude v prvom volaní \(k\) a v každom ďalšom už len menší alebo rovnaký, teda stále bude medzi \(0\) a \(k\). Parameter \(Z\) bude v prvom volaní funkcie \(0\) a v ďalších volaniach bude rásť. Nikdy však nebude väčší, než počet všetkých tyčiniek v automate. Označme si počet tyčiniek najpočetnejšieho druhu (najväčšie z čísel \(p_1, \dots, p_n\) ) ako \(P\). Potom môžeme parameter \(Z\) zhora odhadnúť číslom \(n P\). Naše pole s výsledkami funkcie o(X, Y, Z) teda bude mať veľkosť \((n+1) \times (k+1) \times (n P + 1)\).

Zložitosť

Akú zložitosť má tento algoritmus? Pamäťová zložitosť je jednoduchá: najviac pamäte zaberie naša tabuľka s výsledkami, ktorá má veľkosť \(O(n^2 k P)\). Pri časovej zložitosti potrebujeme sčítať časy všetkých volaní funkie o(X, Y, Z). Tie si môžeme rozdeliť na dve skupiny:

• Volania, pri ktorých sme funkciu naozaj počítali (dané \(X, Y, Z\) sme videli prvýkrát). Takýchto volaní je nanajvýš \(O(n^2 k P)\) (lebo toľko je zmysluplných kombinácií \(X, Y, Z\)) a každé z nich trvá čas \(O(P)\) (musíme vyskúšať všetky možné počty tyčiniek \(X\)-tého druhu). Tieto volania majú teda zložitosť \(O(n^2 k P^2)\).

• Volanie, pri ktorých sme iba vytiahli výsledok z tabuľky. Každé z týchto volaní má zložitosť \(O(1)\). Navyše vieme, že funkciu o(X, Y, Z) sme rekurzívne volali iba vo volaniach prvého druhu, v každom z nich nanajvýš \(P\)-krát. To znamená, že všetkých volaní funkcie \(o(X, Y, Z)\) bolo dokopy nanajvýš \(O(n^2 k P^2)\) a teda volaní druhého druhu mohlo byť tiež nanajvýš \(O(n^2 k P^2)\). To znamená, že ich časová zložitosť je dokopy \(O(n^2 k P^2)\).

Celý náš algoritmus má teda časovú zložitosť \(O(n^2 k P^2)\).

Jednoduché zlepšenia

Časovú zložitosť nášho algoritmu môžeme zlepšiť, ak si všimneme zopár vecí. Cenu najdrahšieho druhu tyčiniek označme \(C\). Ak má Erik \(P C\) alebo viac peňazí, dokáže kúpiť všetky tyčinky v automate: stačí mu vždy kupovať tyčinku s najvyšším číslom, ktorú automat ešte má. Takýmto spôsobom dostane pri každom nákupe jednu tyčinku z každého druhu (okrem tých, čo sa už minuli), a teda po \(P\) nákupoch bude mať všetky tyčinky.

To znamená, že ak \(k \geq P C\), nemusíme volať našu rekurzívnu funkciu, ale stačí nám iba sčítať ceny všetkých tyčiniek. Vďaka tomu nebudeme nikdy volať funkciu o(X, Y, Z) s parametrom \(Y\) väčším ako \(P C\), teda nám aj stačí tabuľka s výsledkami veľkosti \((n+1) \times (P C + 1) \times (n P + 1)\) (pri obmedzeniach \(k \leq 200\,000\) a \(P, C \leq 50\), ktoré boli v praktickom testovaní, je to zlepšenie).

Ďalej si môžeme všimnúť, že ak kúpime \(P\) alebo viac tyčiniek druhov \(X+1, \dots, n\), potom už automaticky dostaneme všetky tyčinky druhov \(1, \dots, X\). To znamená, že našu funkciu nemá zmysel volať s paramtrom \(Z\) väčším ako \(P\). Našu tabuľku teda môžeme zmenšiť na \((n+1) \times (P C + 1) \times (P+1)\).

Týmito dvoma zlepšeniami stlačíme pamäťovú zložitosť na \(O(n P^2 C)\) a časovú na \(O(n P^3 C)\). Toto stačilo na plný počet bodov v praktickom testovaní.

Zložitejšie zlepšenie

Zoberme si nejaké fixné čísla \(X, Y, Z\). V našom výpočte \(o(X, Y, Z)\) počítame v cykle maximum z čísel

\[c_X \min(Z + k, p_X) + o(X-1, Y-k c_X, Z + k)\]

pre \(k\) od \(0\) po \(p_X\), resp. pokým \(Y-k c_X \geq 0\) a \(Z+k \leq P\). Pri výpočte \(o(X, Y-c_X, Z+1)\) počítame maximum z čísel

\[c_X \min(Z+1 + k, p_X) + o(X-1, Y-c_X - k c_X, Z + 1 + k)\]

pre \(k\) od \(0\) po \(p_X\) (resp. pokým dáva daný výraz zmysel), čo je vlastne presne tá istá postupnosť čísel, akurát posunutá o jeden člen. Pri výpočte \(o(X, Y-2 c_X, Z+2)\) budeme opäť rátať maximum z tej istej postupnosti, posunutej o ďalší člen.

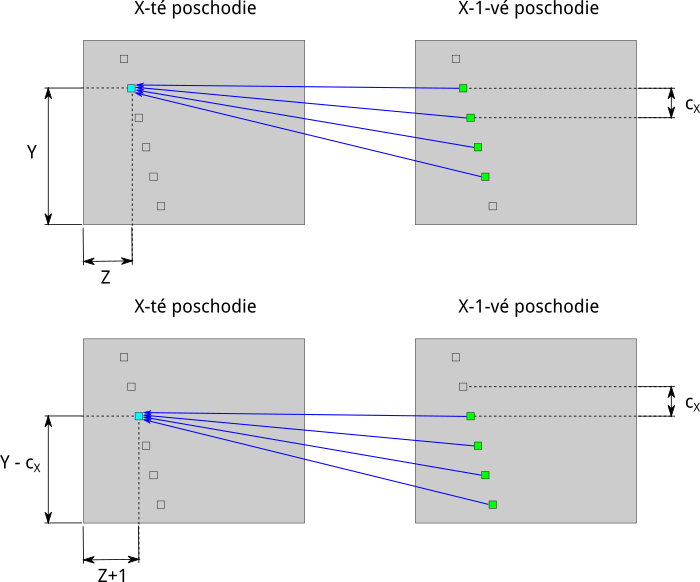
Ak si zoberieme čísla

\[c_X \min(Z + k, p_X) + o(X-1, Y-k c_X, Z + k)\]

pre všetky (aj záporné) \(k\), pre ktoré dáva výraz \(o(X-1, Y-k c_X, Z + k)\) zmysel, dostaneme nejakú postupnosť čísel, označme ju \(T\). Pre každé zmysluplné (aj záporné) \(j\) potom platí, že hodnota \(o(X, Y - j c_X, Z + j)\) je maximum z nejakých \(p_X + 1\) po sebe idúcich členov postupnosti \(T\) (resp., ak sme bližšie než \(p_X\) od konca postupnosti, tak maximum všetkých členov od nejakého bodu až do konca). V úlohe 6 predchádzajúceho kola sme si ukázali, ako sa dajú v lineárnom čase spočítať maximá všetkých \(l\)-tíc po sebe idúcich členov nejakej postupnosti. To môžeme urobiť pre \(l = p_X + 1\). Ak teda poznáme hodnoty prvkov postupnosti \(T\), všetky hodnoty \(o(X, Y - j c_X, Z + j)\) (pre zmysluplné \(j\)) dokážeme spočítať v čase lineárnom od ich počtu. To je rovnako dobré, ako keby sme vedeli funkciu \(o\) v jednom z týchto bodov spočítať za konštantný čas.

Vylepšený algoritmus teda bude vyzerať nasledovne:

• Tabuľku s hodnotami o(X, Y, Z) budeme vypĺňať postupne po “poschodiach”: najprv vyplníme všetky hodnoty, kde \(X = 0\), potom hodnoty kde \(X = 1\) atď.
• Pri vypĺnaní jedného poschodia:
  • Najprv si jednotlivé políčka tabuľky rozdelíme do skupín, pričom v jednej skupine budú všetky políčka s indexami tvaru [X][Y - j * c[X]][Z + j] pre nejaké \(Y, Z\).
  • Pre každú skupinu si zostrojíme príslušnú postupnosť \(T\) (na to využijeme predošlé poschodie tabuľky).
  • Následne v lineárnom čase vypočítame hodnotu funkcie o na všetkých indexoch v našej skupine.

Keďže vypočítanie jednej hodnoty \(o(X, Y, Z)\) bude v priemere trvať konštantný čas, celková zložitosť nášho algoritmu je \(O(n P^2 C)\), rovnako ako pamäťová. Pamäťová zložitosť sa dá ešte vylepšiť na \(O(P^2 C)\), ak si nebudeme pamätať celú našu tabuľku, ale iba aktuálne vypĺňané poschodie a poschodie tesne pod ním.

#include <bits/stdc++.h>
using namespace std;

vector<int> maxima_intervalov(vector<int> T, int l)
{
    vector<int> vysledok;
    deque<pair<int, int> > fronta; // dvojice (hodnota, index)
    for(int zaciatok=-(l-1); zaciatok < (int)T.size(); zaciatok++)
    {
        int koniec = zaciatok + l - 1;
        if(koniec < T.size())
        {
            while(!fronta.empty() && fronta.back().first <= T[koniec])
            {
                fronta.pop_back();
            }
            fronta.push_back(pair<int, int>(T[koniec], koniec));
        }
        if(zaciatok >= 0)
        {
            while(fronta.front().second < zaciatok) 
            {
                fronta.pop_front();
            }
            vysledok.push_back(fronta.front().first);
        }
    }
    return vysledok;
}

int main()
{
    int n, k;
    scanf("%d %d", &n, &k);
    vector<int> c(n), p(n);
    int P = 0, C = 0; //maximalny pocet a maximalna cena
    for(int i=0; i<n; i++)
    {
        scanf("%d", &c[i]);
        C = max(C, c[i]);
    }
    for(int i=0; i<n; i++)
    {
        scanf("%d", &p[i]);
        P = max(P, p[i]);
    }
    
    int max_penazi = min(k, P*C);
    vector<vector<int> > predosle_poschodie(max_penazi+1, vector<int> (P+1, 0));
    vector<vector<int> > aktualne_poschodie(max_penazi+1, vector<int> (P+1, -1));
    
    for(int X = 0; X < n; X++)
    {
        for(int Y = 0; Y <= max_penazi; Y++)
        {
            for(int Z = 0; Z <= P; Z++)
            {
                if(Z == 0 || Y + c[X] > max_penazi) // prvy prvok nejakej postupnosti
                {
                    vector<int> T;
                    for(int k = 0; Y - k*c[X] >= 0 && Z+k <= P; k++)
                    {
                        T.push_back(c[X] * min(Z+k, p[X]) + predosle_poschodie[Y - k*c[X]][Z+k]);
                    }
                    vector<int> maxima = maxima_intervalov(T, p[X] + 1);
                    int i = 0;
                    for(int k = 0; Y - k*c[X] >= 0 && Z+k <= P; k++)
                    {
                        aktualne_poschodie[Y - k*c[X]][Z+k] = maxima[i];
                        i++;
                    }
                }
            }
        }
        predosle_poschodie = aktualne_poschodie;
    }
    printf("%d\n", aktualne_poschodie[max_penazi][0]);
    
    return 0;
}