8. Malé preusporiadanie vzorové riešenie

6
*...*.
**.**.
......
.*..*.
...*..
.**..*

ANO
.**...
****..
......
..**..
*.....
...***

3
**.
*.*
.**

NIE

Hrubá sila

Najjednoduchšie (ale zďaleka nie najefektívnejšie) vyriešime úlohu, ako inak, vyskúšaním všetkých možností. Môžeme vyskúšať všetkých \(n!\) možných preusporiadaní stĺpcov, pre každé preusporiadanie skonštruovať výslednú formáciu a skontrolovať, či táto formácia spĺňa podmienky zo zadania. Časová zložitosť takéhoto riešenia je (pri dobrej implementácii) \(O(n! n^2)\) a v praktickom testovaní by malo zvládnuť prvú sadu vstupov.

Ako vyzerá výsledok?

Ak sa Spartakova armáda dá preusporiadať do formácie spĺňajúcej podmienku zo zadania, aké vlastnosti bude mať výsledná formácia?

Zo zadania vieme, že v každom rade musia vojaci tvoriť jeden súvislý úsek (okrem prázdnych radov, tie ale nie sú zaujímavé, preto sa nimi veľmi zaoberať nebudeme).

Keďže vymieňame iba stĺpce, každý vojak ostane v tom rade, v ktorom začínal. Pre každý rad teda vieme ľahko zistiť, koľko vojakov v ňom je. Inak povedané, vieme, aký dlhý úsek vojakov musí byť v tomto rade.

Ak teda správne určíme, kde sa nacházajú (v ktorom stĺpci začínajú) úseky vojakov v jednotlivých riadkoch, jednoznačne tým určíme celú formáciu.

Pre ľubovoľné dva rady \(A, B\) vieme zistiť, ako veľmi sa budú ich úseky vojakov prekrývať: stačí nám spočítať, koľko je takých stĺpcov, že aj v rade \(A\) aj v rade \(B\) majú vojaka.

Ak sa úseky vojakov v dvoch radoch čiastočne prekrývajú (teda majú aspoň jeden spoločný stĺpec, ale každý z nich má aj stĺpec, ktorý ten druhý nemá), určuje to takmer jednoznačne ich vzájomnú polohu. Ak napríklad máme rad \(A\) so \(7\) vojakmi a rad \(B\) s \(10\) vojakmi, ktorých úseky majú \(4\) spoločné stĺpce, bude ich vzájomná poloha buď takáto:

A: *******......
B: ...**********

alebo takáto:

A: ......*******
B: **********...

Ak teda poznáme absolútnu polohu jedného úseku (teda vieme, v ktorom stĺpci formácie začína), sú iba dve možnosti, kde môže začínať druhý úsek.

Ak poznáme absolútnu polohu dvoch čiastočne sa prekrývajúcich úsekov \(A, B\) a niekto nám dá tretí úsek \(C\), ktorý sa čiastočne prekrýva s úsekom \(A\), dokážeme už presne určiť polohu úseku \(C\):

• Z toho, že \(C\) sa čiastočne kryje s \(A\), máme iba dve možnosti, kde môže začínať \(C\).
• Podľa toho, koľko spoločných stĺpcov majú úseky \(B\) a \(C\) vieme zistiť, ktorá z týchto dvoch možností je správna.

Ak by napríklad úseky \(A\) a \(B\) z vyššie uvedeného príkladu boli umiestnené takto:

A: ....*******.........
B: .......**********...

a vo formácii by bol aj úsek \(C\) dĺžky \(6\), ktorý sa s \(A\) prekrýva v piatich stĺpcoch a s \(B\) v dvoch stĺpcoch, \(C\) musí byť umiestnený takto:

A: ....*******.........
B: .......**********...
C: ...******...........

Nakoniec si ešte všimnime dve veci:

• Ak je nejaká formácia riešením našej úlohy (dá sa vytvoriť preusporiadaním stĺpcov pôvodnej formácie a každý jej neprázdny riadok obsahuje súvislý úsek vojakov), potom aj jej zrkadlový obraz je riešenie.
• Ak formácia vyhovuje podmienkam zo zadania a obsahuje prázdne stĺpce, potom môžeme všetky tieto stĺpce presunúť úplne doprava a znovu dostaneme formáciu, ktorá je riešením.

Zárodok algoritmu

Na základe týchto pozorovaní už môžeme postaviť efektívny algoritmus, ktorý dokáže riešiť niektoré vstupy:

1. Pre každý riadok si spočítame, aký dlhý bude jeho úsek vojakov. Pri prázdnych riadkoch nie je čo riešiť – musia ostať prázdne. Ďalej sa už budeme zaoberať iba neprázdnymi riadkami.
2. Vezmeme si nejaký riadok \(\boldsymbol{A}\) a začiatok jeho úseku vojakov umiestnime predbežne do stĺpca \(\boldsymbol{0}\). Toto ešte nie je jeho finálne umiestnenie vo formácii. Ak v nasledujúcich krokoch umiestnime začiatok nejakécho úseku do stĺpca \(x\), myslíme tým, že vo finálnej formácii bude tento úsek začínať \(x\) stĺpcov napravo od začiatku úseku \(A\). Preto má zmysel hovoriť aj o stĺpcoch so zápornými číslami.
3. Nájdeme iný riadok \(\boldsymbol{B}\), ktorý sa čiastočne prekrýva s \(\boldsymbol{A}\) a na základe ich prekryvu umiestnime úsek \(\boldsymbol{B}\) jedným z dvoch možných spôsobov (je jedno ktorým). Od tohto momentu ďalej si budeme pre každý umiestnený riadok pamätať odkaz na jeho kotvu – iný umiestnený riadok, s ktorým sa čiastočne prekrýva. Kotvou riadku \(\boldsymbol{A}\) bude \(\boldsymbol{B}\) a kotvou \(\boldsymbol{B}\) bude \(\boldsymbol{A}\).
4. Kým sa dá, opakujeme nasledujúce kroky:
   1. Nájdeme riadok nejaký \(\boldsymbol{R}\), ktorý sme ešte nikam neumiestnili, ale čiastočne sa prekrýva s nejakým už umiestneným riadkom \(\boldsymbol{S}\).
   2. Na základe prekryvu \(\boldsymbol{R}\) s \(\boldsymbol{S}\) a s kotvou riadku \(\boldsymbol{S}\) jednoznačne umiestnime úsek v riadku \(\boldsymbol{R}\). Môže sa stať, že neexistuje ani jeden vhodný spôsob umiestnenia \(R\) – vtedy hneď vieme, že Spartakova armáda sa nedá dobre preusporiadať.
   3. Za kotvu riadka \(\boldsymbol{R}\) vezmeme riadok \(\boldsymbol{S}\).
5. Ak sme mali šťastie a vstup bol dobrého tvaru, v kroku 4 sa nám podarilo umiestniť úseky vojakov vo všetkých riadkoch. Všetky úseky posunieme o rovnaký kus doprava tak, aby najľavejší z nich začínal v stĺpci \(\boldsymbol{0}\). Tým dostaneme ich finálne umiestnenie vo formácii.

Ak pre daný vstup existovala aspoň jedna vyhovujúca formácia, my sme určite zostrojili niektorú z nich: pri umiestňovaní väčšiny riadkov sme si vybrali jedinú možnosť, ktorá mala šancu byť správna.

Vynímkou bol riadok \(B\), kde sme si vyberali z dvoch symetrických možností. Ak však existovala vyhovujúca formácia, kde bol riadok \(B\) umiestnený jedným zo spôsobov, potom symetrická formácia bola tiež vyhovujúca a \(B\) je v nej umiestnený druhým spôsobom. Preto bolo naozaj jedno, čo sme si vybrali.

Druhým miestom v našom algoritme, kde nevyberáme jedinú možnú správnu možnosť je krok 5. Ak však existuje nejaká vyhovujúca formácia, potom určite existuje aj taká, kde najľavejší úsek začína v nultom stĺpci (napríklad môžeme zobrať formáciu, kde sú všetky prázdne stĺpce úplne napravo).

Mohlo sa však stať, že daný vstup sa nedá vhodne preusporiadať a my sme napriek tomu niečo vytvorili. Preto ešte musíme overiť, že naša formácia mohla vzniknúť z pôvodnej:

1. Najprv overíme, že každý úsek vojakov končí najneskôr v stĺpci \(\boldsymbol{n-1}\). Ak nie, potom sa naša formácia nezmestí do štvorca \(n \times n\) a teda je určite nesprávna.
2. Ešte potrebujeme overiť, že naša formácia sa skladá z rovnakých stĺpcov ako pôvodná. To zistíme tak, že utriedime jej stĺpce a utriedime aj stĺpce pôvodnej formácie. Ak sa formácie skladali z rovnakých stĺpcov, po utriedení už budú úplne identické (a to vieme overiť ľahko).

Jediným problémom tohto algoritmu je, že funguje, iba ak sa mu v kroku 4 podarí umiestniť všetky úseky vojakov (alebo ak sa mu v tomto kroku podarí zistiť, že sa to nedá).

Vzorové riešenie

V predošlom algoritme sa nám nemusí podariť umiestniť všekty úseky. V takom prípade nám neumiestnené ostanú iba úseky, ktoré sa s umiestnenými úsekmi prekrývajú buď úplne, alebo vôbec. Neumiestnený úsek \(X\) môže vyzerať tromi rôznymi spôsobmi:

1. Úsek \(X\) sa vôbec neprekrýva so žiadnym umiestneným úsekom (nemajú spoločné stĺpce).
2. Úsek \(X\) úplne prekrýva nejaký umiestnený úsek (všetky stĺpce daného úseku sú zároveň stĺpcami \(X\), ale \(X\) má aj nejaké ďalšie stĺpce). V takom prípade už musí \(X\) prekrývať úplne všetky umiestnené úseky (inak by sa s niektorým z nich čiastočne prekrýval – rozmyslite si!).
3. Úsek \(X\) je úplne obsiahnutý v niektorých (aspoň jednom) umiestnených úsekoch, s ostatnými (tých môže byť aj nula) sa vôbec neprekrýva.

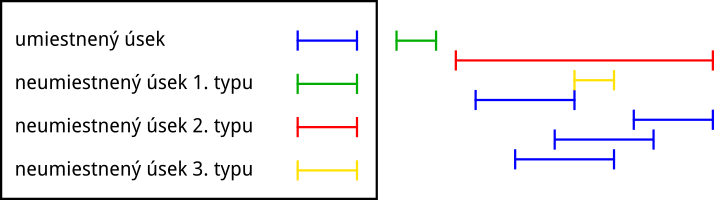
Vzniku úsekov druhého typu vieme predísť tým, že si v prvom kroku algoritmu za úsek \(A\) zvolíme najdlhší úsek vo formácii.

Zvyšné dva druhy (prvý a tretí) sa dajú šikovne vyriešiť rekurziou.

Neumiestnené úseky prvého typu sa neprekrývajú s umiestnenými úsekmi, ani s úsekmi tretieho typu. Od týchto sú teda úplne nezávislé. Medzi sebou sa však prekrývať môžu. Poumiestňujeme ich tak, že celý algoritmus rekurzívne zavoláme iba na úseky prvého typu a následne ich posunieme tesne napravo od predtým umiestnených úsekov.

Ostáva nám ešte vyriešiť neumiestnené úseky tretieho typu. Všetky tieto úseky sa budú celé nachádzať niekde medzi začiatkom najľavejšieho umiestneného úseku a koncom najpravejšie umiestneného úseku. Ak máme \(k\) umiestnených úsekov, pozície ich začiatkov a koncov nám tento interval rozdeľujú na nanajvýš \(2 k - 1\) chlievikov. Každý neumiestnený úsek tretieho typu bude celý vnútri niektorého z týchto chlievikov (inak by sa s nejakým umiestneným úsekom čiastočne prekrýval). Na základe toho, s ktorými umiestnenými úsekmi sa neumiestnené úseky prekrývajú, ich vieme rozdeliť do jednotlivých chlievikov. Ešte potrebujeme umiestniť úseky v rámci ich chlievikov. Na to môžeme pre každý chlievik opäť rekurzívne zavolať náš algoritmus na úseky, ktoré v tomto chlieviku majú byť. Výsledok tohto rekurzívneho volania potom posunieme tak, aby začínal na začiatku chlievika.

Implementácia a zložitosť

Pri implementácii nášho algoritmu si môžeme na začiatku pre každé dva riadky predrátať, v koľkých stĺpcoch majú oba riadky vojaka. To môžeme urobiť priamočiaro v čase \(O(n^3)\). Následne už vieme v konštantnom čase pre ľubovoľné dva riadky zistiť, akým spôsobom sa prekrývajú (čiastočne, vôbec, jeden prekrýva druhý, …).

Na to, ako v kroku 4 hľadáme úseky, ktoré sa čiastočne prekrývajú s už umiesnenými úsekmi, sa dá pozerať ako na prehľadávanie grafu: vrcholmi sú riadky formácie, hrana je medzi dvoma vrcholmi práve vtedy, keď sa ich úseky čiastočne prekrývajú. Tak ho aj môžeme implementovať, takže hľadanie čiastočne sa prekrývajúcich úsekov nám zaberie \(O(n^2)\) času (lebo náš graf je hustý – môže mať až rádovo \(n^2\) hrán).

Ostatné kroky algoritmu by už mali byť pomerne jasné.

Poďme sa teraz pozrieť na zložitosť. Predrátanie prekryvov riadkov robíme len raz za život a trvá \(O(n^3)\) času. Okrem toho máme nejaký rekurzívny algoritmus, ktorý keď zavoláme na \(k\) riadkov, urobí \(O(k^2)\) roboty¹, čím umiestni niektoré riadky (aspoň jeden) a na zvyšné sa nejakým spôsobom rekurzívne zavolá. Keďže v každom rekurzívnom zavolaní umiestnime aspoň jeden riadok, volaní bude dokopy nanajvýš \(n\). Keďže v každom z nich urobíme nanajvýš \(O(n^2)\) roboty, dokopy to bude \(O(n^3)\)². Na konci ešte overujeme, či sme naozaj zostrojili riešenie nášho problému. Pri tejto kontrole najdlhšie trvá triedenie stĺpcov formácie, ktoré zaberie \(O(n^2 \log n)\) času (na utriedenie \(n\) prvkov potrebujeme \(O(n \log n)\) porovnaní a jedno porovnanie môže trvať pri najhoršom \(O(n)\)). Celý náš algoritmus teda beží v čase \(O(n^3)\).

Čo sa týka pamäte, pomerne ľahko sa dá vidieť, že nám bude stačiť \(O(n^2)\) pamäte.

#include <bits/stdc++.h>
using namespace std;
#define inf 1023456789

vector<vector<int> > prienik;

struct riadok {
	int id;
	int vojakov;
	int zaciatok, koniec;
	riadok *kamarat;
	
	riadok(string s, int _id) {
		id = _id;
		vojakov = 0;
		for(int i=0; i<s.size(); i++) {
			if(s[i] == '*') vojakov++;
		}
		zaciatok = -1;
		koniec = -1;
		kamarat = NULL;
	}
	
	string vypis(int n) {
		string s;
		for(int i=0; i<n; i++) {
			if(i >= zaciatok && i < koniec) s.push_back('*');
			else s.push_back('.');
		}
		return s;
	}
	
	bool umiestni(riadok* kamos);
	
	void posun(int delta) {
		zaciatok += delta;
		koniec += delta;
	}
};

int prekryv(riadok *a, riadok *b) {
	return prienik[a->id][b->id];
}

bool riadok::umiestni(riadok* kamos) {
	if(kamos == NULL) {
		zaciatok = 0;
		koniec = vojakov;
		return true;
	}
	int p = prekryv(this, kamos);
	kamarat = kamos;
	zaciatok = kamos->koniec - p;
	koniec = zaciatok + vojakov;
	if(kamos->kamarat == NULL) {
		kamos->kamarat = this;
		return true;
	}
	int p2 = prekryv(this, kamos->kamarat);
	int realny_prekryv = max(min(koniec, kamos->kamarat->koniec) - max(zaciatok, kamos->kamarat->zaciatok), 0);
	if(p2 == realny_prekryv) return true;
	koniec = kamos->zaciatok + p;
	zaciatok = koniec - vojakov;
	realny_prekryv = max(min(koniec, kamos->kamarat->koniec) - max(zaciatok, kamos->kamarat->zaciatok), 0);
	if(p2 == realny_prekryv) return true;
	return false;
}

bool ciastocny_prekryv(riadok* a, riadok* b) {
	int p = prekryv(a, b);
	return p > 0 && p < a->vojakov && p < b->vojakov;
}

int spolocnych(string a, string b) {
	int res = 0;
	for(int i=0; i<a.size(); i++) {
		res += (a[i] == '*' && b[i] == '*');
	}
	return res;
}

bool vyries(vector<riadok*> r) {
	if(r.size() == 0)return true;
	pair<int, int> najdlhsi(-1, -1);
	for(int i=0; i<r.size(); i++) {
		najdlhsi = max(najdlhsi, pair<int, int>(r[i]->vojakov, i));
	}
	vector<riadok*> hotove;
	swap(r[najdlhsi.second], r.back());
	r.back()->umiestni(NULL);
	hotove.push_back(r.back());
	r.pop_back();
	for(int i=0; i<hotove.size(); i++) {
		for(int j=0; j<r.size(); j++) {
			if(ciastocny_prekryv(hotove[i], r[j])) {
				if(!(r[j]->umiestni(hotove[i]))) return false;
				hotove.push_back(r[j]);
				swap(r[j], r.back());
				r.pop_back();
				j--;
			}
		}
	}
	int minsur = inf, maxsur = -inf;
	for(int i=0; i<hotove.size(); i++) {
		minsur = min(minsur, hotove[i]->zaciatok);
	}
	for(int i=0; i<hotove.size(); i++) {
		hotove[i]->posun(-minsur);
		maxsur = max(maxsur, hotove[i]->koniec);
	}
	vector<pair<pair<int, int>, riadok*> > podla_intervalu;
	for(int i=0; i<r.size(); i++) {
		int zac = -1, kon = -1;
		for(int j=0; j<hotove.size(); j++) {
			if(prekryv(r[i], hotove[j]) > 0) {
				if(zac == -1 && kon == -1) {
					zac = hotove[j]->zaciatok;
					kon = hotove[j]->koniec;
				}
				else {
					zac = max(zac, hotove[j]->zaciatok);
					kon = min(kon, hotove[j]->koniec);
				}
			}
		}
		if(zac != -1) {
			for(int j=0; j<hotove.size(); j++) {
				if(prekryv(hotove[j], r[i]) == 0) {
					if(hotove[j]->zaciatok <= zac) {
						zac = max(zac, hotove[j]->koniec);
					}
					if(hotove[j]->koniec >= kon) {
						kon = min(kon, hotove[j]->zaciatok);
					}
				}
			}
		}
		podla_intervalu.push_back(make_pair(make_pair(zac, kon), r[i]));
	}
	sort(podla_intervalu.begin(), podla_intervalu.end());
	vector<riadok*> skupina;
	int zac = -2, kon = -2;
	for(int i=0; i<podla_intervalu.size(); i++) {
		if(podla_intervalu[i].first == make_pair(zac, kon)) {
			skupina.push_back(podla_intervalu[i].second);
		}
		else {
			if(skupina.size() > 0) {
				if(!vyries(skupina)) return false;
				int pos = zac == -1 ? maxsur : zac;
				for(int j=0; j<skupina.size(); j++) {
					skupina[j]->posun(pos);
				}
				skupina.clear();
			}
			zac = podla_intervalu[i].first.first;
			kon = podla_intervalu[i].first.second;
			skupina.push_back(podla_intervalu[i].second);
		}
	}
	if(skupina.size() > 0) {
		if(!vyries(skupina)) return false;
		int pos = zac == -1 ? maxsur : zac;
		for(int j=0; j<skupina.size(); j++) {
			skupina[j]->posun(pos);
		}
	}
	return true;
}

vector<string> normalizuj(vector<string> formacia) {
	int n = formacia.size();
	vector<string> vysledok(n);
	for(int x=0; x<n; x++) {
		for(int y=0; y<n; y++) {
			vysledok[x].push_back(formacia[y][x]);
		}
	}
	sort(vysledok.begin(), vysledok.end());
	return vysledok;
}

bool over(vector<string> vstup, vector<string> vystup) {
	return normalizuj(vstup) == normalizuj(vystup);
}

int main() {
	int n;
	cin >> n;
	string pom;
	getline(cin, pom);
	
	vector<string> vstup(n);
	vector<riadok*> vsetky;
	vector<riadok*> neprazdne;
	for(int y=0; y<n; y++) {
		getline(cin, vstup[y]);
		vsetky.push_back(new riadok(vstup[y], y));
		if(vsetky.back()->vojakov > 0) {
			neprazdne.push_back(vsetky.back());
		}
	}
	
	prienik.resize(n, vector<int> (n,0));
	for(int i=0; i<n; i++) {
		for(int j=i+1; j<n; j++) {
			prienik[i][j] = prienik[j][i] = spolocnych(vstup[i], vstup[j]);
		}
	}
	
	if(!vyries(neprazdne)) {
		cout << "NIE" << endl;
		return 0;
	}
	
	vector<string> vysledok(n);
	for(int y=0; y<n; y++)vysledok[y] = vsetky[y]->vypis(n);
	if(!over(vstup, vysledok)) {
		cout << "NIE" << endl;
		return 0;
	}
	cout << "ANO" << endl;
	for(int y=0; y<n; y++) {
		cout << vysledok[y] << endl;
	}
	
	prienik.resize(n, vector<int> (n));
	return 0;
}

Lepšie riešenia

Táto úlohá má aj riešenie v \(O(n^2)\), je však nad rámec tohoto textu a na plný počet bodov ho nebolo treba. Môžete sa však zamyslieť nad nasledovnou otázkou: ako by sa dalo predrátanie prekryvov riadkov (ktoré vo vzoráku robíme v čase \(O(n^3)\)) robiť v čase \(O(n^3 / \log n)\)?