7. Utrápený Michallius vzorové riešenie

4
2 3
3 2
1 1
4 4

3
3
1
4

4
3 3
4 1
1 4
2 2

4
4
4
4

Koľko bitkoinov vie vyhrať gladiátor \(\boldsymbol{a}\)?

Aby sme zistili koľko bitkoinov môže zarobiť nejaký gladiátor \(a\), skúsme najskôr zistiť ktoré bitkoiny môže \(a\) získať.

Aby gladiátor \(a\) získal bitkoin, ktorý na začiatku turnaja patril gladiátorovi \(b\), musí k nemu tento bitkoin nejako doputovať. Táto púť bude vyzerať tak, že najskôr \(b\) prehrá súboj s nejakým iným gladiátorom, ten (ak to ešte nie je gladiátor \(a\)) potom prehrá s ďalším gladiátorom, ten prehrá s ďalším, atď., až nakoniec posledný gladiátor z tejto reťaze prehrá s gladiátorom \(a\).

Povedané formálne, \(a\) dokáže získať bitkoin od \(b\), vtedy a len vtedy, keď existuje postupnosť gladiátorov \(b = g_1, g_2, \ldots, g_k = a\) taká, že pre všetky prípustné \(i\) vie \(g_{i+1}\) poraziť \(g_i\) v aspoň jednom type súboja.

Máme teda dobre popísaný vzťah “\(a\) vie získať bitkoin \(b\)”. Viac bitkoinov než počet takýchto gladiátorov \(b\) gladiátor \(a\) nevie získať. Ale to, že \(a\) vie získať bitkoiny od \(b_1, \ldots, b_m\) ešte neznamená, že ich vie získať všetky v priebehu jedného turnaja. Ukazuje sa ale, že sa to dá.

Dobre sa to vysvetľuje z grafového hľadiska. Uvažujme orientovaný graf, v ktorom vrcholy reprezentujú gladiátorov, a je v ňom hrana \(x \rightarrow y\) vtedy, keď \(x\) vie poraziť \(y\) aspoň v jednom type súboja. Potom \(a\) vie získať bitkoiny práve tých gladiátorov, ktorí sú dosiahnuteľní z \(a\) (rozmyslite si).

Postupnosť zápasov, v ktorej \(a\) získa bitkoiny od všetkých takýchto gladiátorov, vieme nájsť nasledovne:

1. Začneme s prázdnou postupnosťou zápasov.
2. Spustime prehľadávanie (napríklad do hĺbky) z \(a\) a vždy, keď prejdeme po hrane do nejakého ešte nenavštíveného vrcholu, zafarbime túto hranu na červeno. Po skončení prehľadávania budú červené hrany tvoriť strom obsahujúci práve vrcholy dosiahnuteľné z \(a\).
3. Z tohto stromu odstránime hranu \(x \rightarrow y\) vedúcu do listu a do postupnosti pridáme zápas medzi \(x, y\), pričom typ zápasu zvolíme tak, aby \(x\) vyhral.
4. Opakujeme predchádzajúci krok, kým sú v grafe hrany.

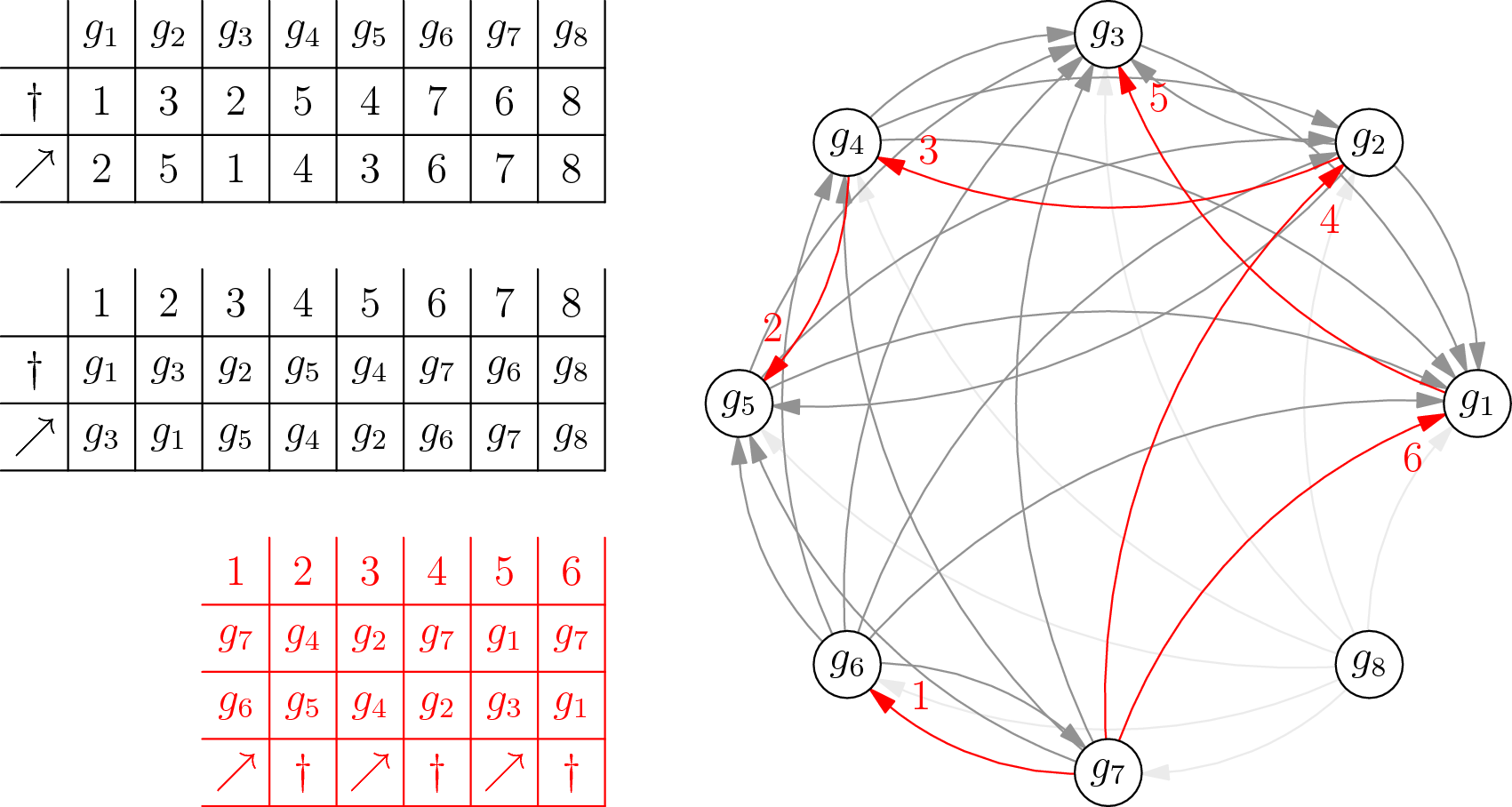
(Prvá tabuľka zobrazuje sily jednotlivých gladiátorov. Druhá tabuľka obsahuje gladiátorov usporiadaných podľa ich síl. Tretia tabuľka zobrazuje zápasy v takom turnaji, v ktorom by gladiátor \(g_7\) získal všetky bitkoiny, ktoré vie získať.)

Prvý správny algoritmus

Predchádzajúca úvaha nám dáva jednoduchý algoritmus na riešenie úlohy: zostrojíme graf a postupne z každého vrcholu \(a\) spustíme prehľadávanie, ktorým zistíme, koľko vrcholov z neho vieme dosiahnuť. To je zároveň aj počet bitkoinov, ktorý si vie gladiátor \(a\) z turnaja odniesť.

Graf obsahuje \(n\) vrcholov a \(O(n^2)\) hrán, časová zložitosť je preto \(O(n^3)\). Pamäťová zložitosť je \(O(n^2)\) (ak v pamäti vytvoríme všetky hrany), prípadne \(O(n)\) (ak si pamätáme iba sily gladiátorov).

#include <bits/stdc++.h>
using namespace std;

vector<vector<int>> graf;
vector<int> navstivene;
int pocet;

void dfs(int v) {
  if (navstivene[v]) return;
  navstivene[v] = true;
  pocet++;

  for (int i = 0; i < graf[v].size(); ++i) {
    dfs(graf[v][i]);
  }
}

int main() {
  int n; scanf("%d", &n);
  vector<int> mec(n), kopija(n);
  navstivene.resize(n);

  for (int i = 0; i < n; ++i) {
    scanf("%d%d", &mec[i], &kopija[i]);
  }

  graf.resize(n);
  for (int i = 0; i < n; ++i) {
    for (int j = 0; j < n; ++j) {
      if (mec[i] > mec[j]) graf[i].push_back(j);
      if (kopija[i] > kopija[j]) graf[i].push_back(j);
    }
  }

  for (int i = 0; i < n; ++i) {
    pocet = 0;
    for(int j = 0;j < n;j++) navstivene[j] = 0;
    dfs(i);
    printf("%d\n", pocet);
  }

  return 0;
}

Predchádzajúce riešenie možno o rád zrýchliť nasledujúcim trikom: usporiadajme si gladiátorov do postupnosti \(g'_1, g'_2, \ldots, g'_n\) podľa rastúcej sily v boji s mečom. Potom nemusíme mať v grafe všetky hrany \(g'_i \rightarrow g'_j\) pre \(i > j\), stačí, ak v ňom budú hrany \(g'_i \rightarrow g'_{i - 1}\) pre všetky prípustné \(i\).

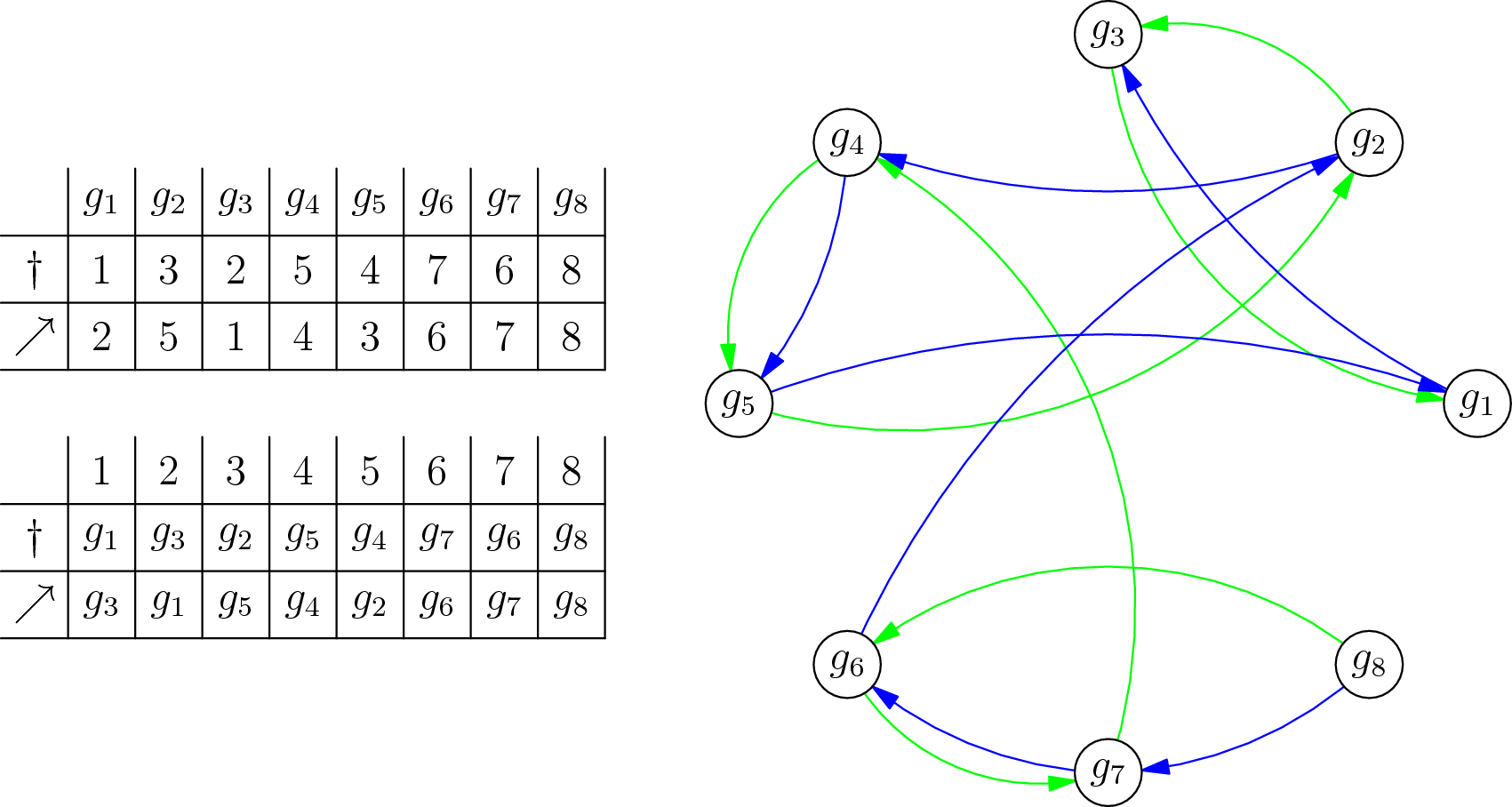
(Graf, v ktorom neuvažujeme zbytočné hrany. Pre každú silu \(k > 1\) a každý typ boja máme hranu vedúcu od gladiátora so silou \(k\) ku gladiátorovi so silou \(k - 1\). Zelené hrany zodpovedajú boju s mečom, modré hrany boju s kopijou.)

Prečo? Ak v pôvodnom grafe existovala cesta z \(a\) do nejakého \(b\), tak v novom grafe dostaneme cestu z \(a\) do \(b\) tak, že každú hranu na pôvodnej ceste, ktorá má tvar \(g_i \rightarrow g_j\) pre \(i > j\), nahradíme postupnosťou hrán \(g_i \rightarrow g_{i - 1}, g_{i - 1} \rightarrow g_{i - 2}, \ldots, g_{j + 1} \rightarrow g_j\). Takže pre ľubovoľný vrchol \(a\) je množina vrcholov dosiahnuteľných z \(a\) rovnaká, ako v pôvodnom grafe.

Rovnako vieme zredukovať počet hrán, ktoré zodpovedajú súbojom s kopijou. V novom grafe budeme mať \(2 \cdot (n - 1) = O(n)\) hrán, a vylepšíme tým časovú zložitosť algoritmu na \(O(n^2)\).

#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;

vector<vector<int>> graf;
vector<int> vysledok, navstivene;
int pocet;

void dfs(int v) {
  if (navstivene[v]) return;
  navstivene[v] = true;
  pocet++;

  for (int i = 0; i < graf[v].size(); ++i) {
    dfs(graf[v][i]);
  }
}

int main() {
  int n; scanf("%d", &n);
  vector<pii> mec(n), kopija(n);
  vysledok.resize(n);
  navstivene.resize(n);

  for (int i = 0; i < n; ++i) {
    scanf("%d%d", &mec[i].first, &kopija[i].first);
    mec[i].second = kopija[i].second = i;
  }
  sort(mec.begin(), mec.end());
  sort(kopija.begin(), kopija.end());
  graf.resize(n);

  for (int i = 1; i < n; ++i) {
    graf[mec[i].second].push_back(mec[i-1].second);
    graf[kopija[i].second].push_back(kopija[i-1].second);
  }

  for (int i = 0; i < n; ++i) {
    pocet = 0;
    for(int j = 0;j < n;j++) navstivene[j] = 0;
    dfs(mec[i].second);
    vysledok[mec[i].second] = pocet;
  }

  for (int i = 0; i < n; ++i) {
    printf("%d\n", vysledok[i]);
  }

  return 0;
}

Vzorové riešenie

Majme gladiátorov \(g_1, g_2, \ldots, g_n\) usporiadaných vzostupne podľa sily v boji s mečom. Všimnime si, že všetky bitkoiny, ktoré vie získať \(g_i\), vie získať aj \(g_{i + 1}\). To ale znamená, že keď hľadáme vrcholy dosiahnuteľné z \(g_{i + 1}\), tak nám stačí hľadať iba také vrcholy, ktoré nie sú dosiahnuteľné z \(g_i\). Vrcholy dosiahnuteľné z \(g_i\) totiž môžeme zarátať automaticky.

Budeme teda púštať prehľadávanie postupne od najslabších gladiátorov k najsilnejším, teda v poradí \(g_1, g_2, \ldots, g_n\). Pre každého gladiátora si pamätáme, či sme ho už v niektorom prehľadávaní navštívili, a pamätáme si tiež počet už navštívených gladiátorov. Keď prehľadávame z \(g_i\), tak nenavštevujeme vrcholy, ktoré sme už navštívili v niektorom z predchádzajúcich prehľadávaní.

Rozmyslite si, že takýmto spôsobom sú po \(i\)-tom prehľadávaní navštívení práve tí gladiátori, ktorí sú dosiahnuteľní z \(g_i\). Práve od nich vie \(g_i\) získať bitkoin. Ich počet je teda počet bitkoinov, ktoré vie \(g_i\) získať.

Zložitosť

Na začiatku si potrebujeme utriediť gladiátorov podľa sily. To nám bude trvať \(O(n \log n)\). Počas prehľadávaní navštívime každý vrchol grafu najviac raz, čo je \(O(n)\) roboty (lebo graf má len \(n\) vrcholov a \(O(n)\) hrán). Preto je časová zložitosť celého algoritmu \(O(n \log n)\). Pamäťová zložitosť ostáva \(O(n)\).

Pritom časová zložitosť \(O(n \log n)\) je iba kvôli triedeniu, my však máme čísla z rozsahu od \(1\) po \(n\). Vieme ich teda utriediť count sortom, a dostaneme tak lepší čas \(O(n)\).

#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;

vector<vector<int>> graf;
vector<int> vysledok, navstivene;
int pocet;

void dfs(int v) {
  if (navstivene[v]) return;
  navstivene[v] = true;
  pocet++;

  for (int i = 0; i < graf[v].size(); ++i) {
    dfs(graf[v][i]);
  }
}

void countSort(vector<pii> &v) {
  vector<pii> utriedene(v.size());
  for (int i = 0; i < v.size(); ++i) {
    utriedene[v[i].first - 1] = v[i];
  }
  v = utriedene;
}

int main() {
  int n; scanf("%d", &n);
  vector<pii> mec(n), kopija(n);
  vysledok.resize(n);
  navstivene.resize(n);

  for (int i = 0; i < n; ++i) {
    scanf("%d%d", &mec[i].first, &kopija[i].first);
    mec[i].second = kopija[i].second = i;
  }
  countSort(mec);
  countSort(kopija);
  graf.resize(n);

  for (int i = 1; i < n; ++i) {
    graf[mec[i].second].push_back(mec[i-1].second);
    graf[kopija[i].second].push_back(kopija[i-1].second);
  }

  for (int i = 0; i < n; ++i) {
    dfs(mec[i].second);
    vysledok[mec[i].second] = pocet;
  }

  for (int i = 0; i < n; ++i) {
    printf("%d\n", vysledok[i]);
  }

  return 0;
}