Zadanie
Ráno bitka, na obed bitka, poobede bitka, večer bitka. Napriek tomu, že sledovať súboj gladiátorov na život a na smrť1 vie byť pomerne zábavný spôsob ako premárniť zopár hodín voľného času2, takýto program miestny ľud rýchlo omrzel.
Cézar dal teda po krajine rozhlásiť, že sa plánuje spestrenie vystúpení v Koloseu – organizuje sa prvý ročník šou Rímska ríša má talent!. Prvé oficiálne kolo bude už o mesiac priamo v Koloseu – a rozhodovať bude samotný cézar.
Farmárovi Denisiovi sa splnil sen. Konečne bude môcť zažiariť a ukázať, čo sa v ňom skrýva. Doteraz sa v Koloseu nemal čím predvádzať – na gladiátorské súboje bol príliš chudý a slabý. Ale s ovcami, s tými si teda rozumie.
Dlhé roky ich vyháňal na pašu a vo voľnom čase ich učil rôzne cirkusové kúsky. Je si však vedomý, že konkurencia bude veľká – už sa šíria chýry o cestujúcom, ktorý vie chodiť po vode. Aby mal šancu na víťazstvo, musí si Denisius nechať svoje najúžasnejšie ovčie kúsky na neskoršie kolá súťaže. Najlepšie by bolo, keby sa do ďalšieho kola dostal s najmenej nacvičeným trikom – ovce priučil jednoduchej geometrii a na jeho povel sa chaotické stádo oviec razom rozostaví na najviac dve priamky.
Pred svojim vystúpením by si chcel tento kúsok so svojimi ovcami ešte precvičiť – ak sa mu nevydarí, určite nepostúpi, a to ho potom cézar dá zožrať levom3. Z hľadiska Kolosea sa výkon jeho oviec hodnotí ľahko, keď však Denisius stojí spolu s ovcami na lúke za dedinou, nevidí, či sa jeho ovce naozaj poslušne postavili na najviac dve priamky. Na to potrebuje vašu pomoc!
Úloha
V Denisiovom stáde je \(n\) oviec. Každú ovcu si môžeme predstaviť ako bod v rovine s celočíselnými súradnicami. Dostanete rozostavenie oviec po tom, čo Denisius zadal povel, aby sa postavili na najviac dve priamky. Zistite, či sa im to podarilo.
Formát vstupu
V prvom riadku je celé číslo \(n\) (\(1 \leq n \leq 2 \cdot 10^5\)) – počet oviec v Denisiovom stáde.
V nasledujúcich \(n\) riadkoch sú po dve celé čísla \(x_i, y_i\) – súradnice \(i\)-tej ovce po tom, čo Denisius dal svoj povel.
Súradnice v absolútnej hodnote neprekročia \(10^9\). Žiadne dve ovce nestoja na rovnakých súradniciach.
Sú štyri sady testovacích vstupov. Maximálne hodnoty \(n\) v jednotlivých sadách sú nasledovné:
| číslo sady | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|
| \(n \leq\) | \(10\) | \(1\,000\) | \(10\,000\) | \(200\,000\) |
Formát výstupu
Ak existujú dve priamky také, že každá ovca stojí aspoň na jednej z nich, vypíšte ANO. Inak vypíšte NIE.
Príklady
Input:
6
0 1
3 4
10 11
5 0
6 2
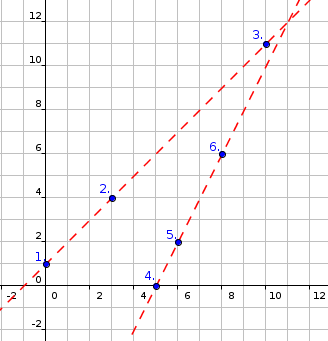
8 6Output:
ANOPrvé tri ovce stoja na jednej priamke, posledné tri na druhej:
Input:
6
0 1
3 4
9 11
5 0
6 2
8 6Output:
NIEPredslov o priamkach
Ešte predtým, ako sa pustíme do samotných algoritmických riešení, musíme vymyslieť ako vlastne budeme reprezentovať priamku a ako potom overíme, či na nej niektorá ovca je alebo nie je.
Priamku si vieme jednoznačne určiť pomocou dvojice bodov, ktoré na nej ležia – v tejto úlohe teda všetky priamky, ktoré nás môžu zaujímať, budú definované dvoma rôznymi ovcami.
V programoch vzorových riešení sme použili nasledovný spôsob: keď máme dve ovce na súradniciach \((x_1,y_1)\) a \((x_2,y_2)\), priamku si vyjadríme ako prvý bod a smernicu od tohto bodu \((x_2 - x_1, y_2 - y_1)\) = \((d_x,d_y)\). Voľne prerozprávané, smernica nám hovorí že za každý krok dĺžky \(d_x\) v kladnom smere \(x\)-ovej osi máme spraviť krok dĺžky \(d_y\) v kladnom smere \(y\)-ovej osi.
Túto smernicu ešte upravíme do nami definovaného kanonického tvaru – vydelíme \(d_x\) a \(d_y\) ich najväčším spoločným deliteľom, ak je \(d_x\) záporné vynásobíme ju \(-1\) (teda našu smernicu chceme mať v ‘kladnom smere’), a ak je \(d_x = 0\) tak chceme \(d_y\) kladné.
Teraz bod patrí na túto priamku, ak je jeho smernica od prvého bodu rovnaká ako tá, ktorou sme si vyjadrili priamku. Teda napríklad pre ovce \((10,15)\) a \((12,25)\) by sme dostali smernicu \((2,10)\), ktorú upravíme do základného tvaru \((1,5)\) – čo voľne prerozprávané znamená, že aby niektorá ovca ležala na tejto priamke, musíme sa k nej vedieť dostať tak že začneme na súradniciach prvej ovce a pohybujeme sa tak, že za každý posun v kladnom smere \(x\) o \(1\) sa posunieme o \(5\) v kladnom smere \(y\) (posun v zápornom smere je analogický). Teraz napríklad bod \((6,-5)\) na túto priamku patrí – jeho smernica k prvému bodu je \((6-10,-5 - 15) = (-4,-20)\) čo sa po upravení do kanonického tvaru (\(\rightarrow (-1,-5) \rightarrow (1,5)\)) rovná smernici ktorú sme prvotne vyrátali. Bod \((8,25)\) na túto priamku nepatrí, keďže jeho smernica je \((8-10,25-15) = (-2,10) \rightarrow (-1,5) \rightarrow (1,-5)\), čo sa našej smernici nerovná.
Inou možnosťou, ktorá vyžaduje trochu viac znalostí stredoškolskej geometrie, je využiť vektorový súčin – o ňom sa môžete dočítať v kuchárke KSP.
Riešenie hrubou silou
Už teda vieme priamku aj reprezentovať, aj overovať, či na nej leží niektorá ovca. Čo nám chýba k riešeniu? Rozmyslieť si, ktoré priamky musíme overiť.
Prvým, najprimitívnejším riešením je jednoducho vyskúšať všetky možné riešenia (dvojice priamok) – zoberieme postupne všetky štvorice oviec na vstupe, určíme prvú priamku pomocou prvých dvoch oviec vo štvorici a druhú priamku pomocou tretej a štvrtej ovce. Následne spôsobom, ktorý nám je milší, vždy overíme, či všetky ovce zo vstupu patria aspoň na jednu z týchto priamok. Ak sa nám to raz podarí, odpovieme ,,áno’’, ak nám to ani raz nevyjde, tak také dve priamky neexistujú – vyskúšali sme predsa všetky možnosti čo pripadali do úvahy.
Štvoríc oviec je rádovo \(O(n^4)\) a overiť pre každú z \(n\) oviec, či leží na aspoň jednej z nich, nám zaberie \(O(n)\), teda dokopy nám to zaberie \(O(n^5)\) času. Pritom nám netreba pamätať si nič viac ako súradnice všetkých oviec, čiže pamätová zložitosť je \(O(n)\).
#include <iostream>
#include <algorithm> // najvacsi spolocny delitel __gcd
#include <vector> // pole ktoremu mozeme za behu menit velkost
using namespace std;
struct ovca
{
int x,y;
};
// upravi smernicu priamky do kanonickeho tvaru
ovca zakladny_tvar(ovca vektor)
{
// vydelime dx,dy najvacsim spolocnym delitelom
int gcd = __gcd(vektor.x,vektor.y);
vektor.x /= gcd;
vektor.y /= gcd;
// v kanonickom tvare chceme dx kladne
if(vektor.x < 0)
{
vektor.x *= -1;
vektor.y *= -1;
}
else if (vektor.x == 0) // ak je dx 0, chceme dy kladne
vektor.y = abs(vektor.y);
return vektor;
}
int n;
vector<ovca> stado;
int main()
{
cin >> n;
if(n<=4)
{
cout << "ANO\n";
return 0;
}
stado.resize(n);
for(int i=0;i<n;++i)
cin >> stado[i].x >> stado[i].y;
// budeme skusat priamku urcenu ovcami 0 a i.
for(int i=0;i<n;++i)
{
for(int j=i+1;j<n;++j)
{
for(int k=j+1;k<n;++k)
{
for(int l=k+1;l<n;++l)
{
ovca prva = {stado[j].x-stado[i].x,stado[j].y-stado[i].y};
prva = zakladny_tvar(prva);
ovca druha = {stado[l].x-stado[k].x,stado[l].y-stado[k].y};
druha = zakladny_tvar(druha);
for(int m=0;m<n;++m)
{
if(m==i || m==k) continue;
ovca vektor_k_prvej = {stado[m].x-stado[i].x,stado[m].y-stado[i].y};
vektor_k_prvej = zakladny_tvar(vektor_k_prvej);
ovca vektor_k_druhej = {stado[m].x-stado[k].x,stado[m].y-stado[k].y};
vektor_k_druhej = zakladny_tvar(vektor_k_druhej);
// ak sa ovca cislo m nenachadza ani na jednej z priamok, prestaneme overovat a zacneme skusat dalsiu priamku
if( (vektor_k_prvej.x != prva.x || vektor_k_prvej.y != prva.y) && (vektor_k_druhej.x != druha.x || vektor_k_druhej.y != druha.y) )
break;
// vsetky ovce lezia na aspon jednej priamke
if(m==n-1)
{
cout << "ANO\n";
return 0;
}
}
}
}
}
}
// ani raz sme nenasli riesenie, povieme nie
cout << "NIE\n";
return 0;
}Riešenie polohrubou silou
Horeuvedené riešenie vieme jednoduchým pozorovaním vylepšiť. Zoberme si ľubovoľnú ovcu – pre jednoduchosť pokojne prvú zo vstupu. Ak všetky ovce sú na najviac dvoch priamkach, tak aj táto ovca je na jednej z nich. A na akej priamke môže byť? No na priamke určenej ňou a druhou ovcou, alebo ňou a treťou ovcou, …, alebo ňou a poslednou ovcou. Postupne pre každú ovcu okrem prvej si teda určíme priamku (označme ju \(p\)) pomocou nej a prvej ovce a overíme ktoré ďalšie ovce na nej stoja.
No a teraz si stačí uvedomiť, že všetky ovce, ktoré neležia na priamke \(p\), musia byť na jednej inej priamke \(q\) – tá bude teda určená ľubovoľnými dvomi z nich (napríklad prvými dvomi, o ktorých pri overovaní zistíme, že nepatria na priamku \(p\)). Zoberieme si teda priamku \(q\) a opäť prejdeme všetky ovce (prípadne len tie, o ktorých sme zistili, že neležia na priamke \(p\), ak sme si ich niekam ukladali) – ak potom všetky ovce patria na nejakú priamku (\(p\) alebo \(q\)), zahlásime Denisiov úspech. Inak opäť od začiatku skúšame novú priamku \(p\) určenú prvou a ďalšiou ovcou. Ak bez úspechu vyskúšame všetky možné priamky \(p\), odpovieme nakoniec ,,nie’’.
O koľko sme naše riešenie urýchlili? V prípade, že riešenie neexistuje, vyskúšame rádovo \(n\) priamok \(p\) – priamku určenú prvou a druhou ovcou, prvou a treťou, … , prvou a \(n\)-tou ovcou. Zakaždým prejdeme všetkých \(n\) oviec a overíme či ležia na priamke \(p\). Následne určíme priamku \(q\) a pre všetky (zvyšné) ovce overíme, či na nej ležia. Aj toto je v najhoršiom prípade zhruba \(n\) oviec. Keďže \(n\) krát môžeme robiť až \(n\) operácií, výsledný odhad časovej zložitosti v najhoršiom prípade je \(O(n^2)\). Teraz si už musíme aj zakaždým pamätať, ktoré ovce nestoja na priamke \(p\), ktorú práve skúšame. To nám však zaberie len \(O(n)\) pamäte, pamäťová zložitosť je teda opäť \(O(n)\).
#include <iostream>
#include <algorithm> // najvacsi spolocny delitel __gcd
#include <vector> // pole ktoremu mozeme za behu menit velkost
using namespace std;
struct ovca
{
int x,y;
};
// upravi smernicu priamky do kanonickeho tvaru
ovca zakladny_tvar(ovca vektor)
{
// vydelime dx,dy najvacsim spolocnym delitelom
int gcd = __gcd(vektor.x,vektor.y);
vektor.x /= gcd;
vektor.y /= gcd;
// v kanonickom tvare chceme dx kladne
if(vektor.x < 0)
{
vektor.x *= -1;
vektor.y *= -1;
}
else if (vektor.x == 0) // ak je dx 0, chceme dy kladne
vektor.y = abs(vektor.y);
return vektor;
}
int n;
vector<ovca> stado;
vector<bool> napriamke;
// oznaci vsetky ovce ktore lezia na priamke urcenej ovcami a,b.
// ak je 'prva', skusi overit ci su zvysne ovce na priamke urcenej prvymi
// dvoma ovcami ktore na nu nepatria. ak to je uz druha priamka a stale su ovce
// neleziace na priamke, uz vrati zapornu odpoved.
bool over_na_priamke(int a,int b,bool prva)
{
napriamke[a] = napriamke[b] = true;
// toto je priamka urcena ovcami a,b
ovca vektor = {stado[b].x-stado[a].x,stado[b].y-stado[a].y};
vektor = zakladny_tvar(vektor);
// sem dame vsetky ovce ktore nelezia na ziadnej skusanej priamke
vector<int> zle;
for(int i=0;i<n;++i)
{
if(i==a || i==b) continue;
ovca tmp = {stado[i].x-stado[a].x,stado[i].y-stado[a].y};
tmp = zakladny_tvar(tmp);
// ak je ovca cislo i na rovnakej priamke ako a,b oznacime ju
// inak, ak nie je oznacena ako na priamke, ju pridame do zoznamu oviec ktore niesu na ziadnej skusanej priamke
if(vektor.x == tmp.x && vektor.y == tmp.y)
napriamke[i] = true;
else if(!napriamke[i]) zle.push_back(i);
}
// ak uz skusame druhu priamku, musime mat 0 zlych oviec
if(!prva) return zle.empty();
// ak mame najviac 2 ovce, nasli sme riesenie
if(zle.size()<=2) return true;
// skusime overit ci vsekty zvysne ovce lezia na priamke urcenej prvymi dvoma zlymi ovcami
return over_na_priamke(zle[0],zle[1],false);
}
int main()
{
cin >> n;
if(n<=4)
{
cout << "ANO\n";
return 0;
}
stado.resize(n);
napriamke.resize(n);
for(int i=0;i<n;++i)
cin >> stado[i].x >> stado[i].y;
// budeme skusat priamku urcenu ovcami 0 a i.
for(int i=1;i<n;++i)
{
// kazdu ovcu oznacime ako neleziacu na priamke
for(int j=0;j<n;++j)
napriamke[j] = false;
// ak najdeme riesenie, hned povieme ano a skoncime
if(over_na_priamke(0,i,true))
{
cout << "ANO\n";
return 0;
}
}
// ani raz sme nenasli riesenie, povieme nie
cout << "NIE\n";
return 0;
}Vzorové riešenie – ešte menej priamok!
Stále ešte overujeme príliš veľa priamok. K vzorovému riešeniu nás privedie pozorovanie podobné tomu, ktoré sme spravili v predošlom riešení. Zoberme si ľubovoľné tri ovce – pre jednoduchosť prvé tri zo vstupu. Predpokladajme, že ovce naozaj stoja na najviac dvoch priamkach a predstavme si, že pre každú ovcu si zaznačíme či leží na prvej alebo na druhej (alebo na oboch, toto však nerobí rozdiel), a pozrime sa na naše tri ovce. Sú len dve možnosti – buď všetky tri naše ovce ležia na spoločnej priamke (ktorá je jedna z dvoch, na ktorých ležia všetky ovce), alebo dve ovce ležia na jednej z našich dvoch priamok a tretia leží na druhej. V oboch prípadoch platí, že na jednej z priamok stoja aspoň dve z našich troch oviec. Povedané inak, nemôže sa stať, že by existovali dve priamky (také že všetky ovce stoja aspoň na jednej z nich), bez toho aby niektoré dve ovce z našich troch stáli na jednej z nich.
Vzorové riešenie je teda skoro rovnaké ako predošlé – overíme však len tri možné priamky \(p\):
- Priamku určenú prvou a druhou ovcou
- Priamku určenú prvou a treťou ovcou
- Priamku určenú druhou a treťou ovcou
Toto overovanie urobíme rovnako ako v minulom riešení. Ak ani jedna z týchto priamok neuspeje, môžeme spokojne oznámiť, že ovce nestoja na najviac dvoch priamkach.
Overenie priamky nám, neprekvapivo, ešte stále zaberie \(O(n)\) času, skúšame ich však iba tri – čiže konštantne veľa. Časová zložitosť je teda \(O(n)\). Pamäť využívame úplne rovnako ako v predošlom riešení, čiže tá je aj do tretice \(O(n)\).
#include <iostream>
#include <algorithm> // najvacsi spolocny delitel __gcd
#include <vector> // pole ktoremu mozeme za behu menit velkost
using namespace std;
struct ovca
{
int x,y;
};
// upravi smernicu priamky do kanonickeho tvaru
ovca zakladny_tvar(ovca vektor)
{
// vydelime dx,dy najvacsim spolocnym delitelom
int gcd = __gcd(vektor.x,vektor.y);
vektor.x /= gcd;
vektor.y /= gcd;
// v kanonickom tvare chceme dx kladne
if(vektor.x < 0)
{
vektor.x *= -1;
vektor.y *= -1;
}
else if (vektor.x == 0) // ak je dx 0, chceme dy kladne
vektor.y = abs(vektor.y);
return vektor;
}
int n;
vector<ovca> stado;
vector<bool> napriamke;
// oznaci vsetky ovce ktore lezia na priamke urcenej ovcami a,b.
// ak je 'prva', skusi overit ci su zvysne ovce na priamke urcenej prvymi
// dvoma ovcami ktore na nu nepatria. ak to je uz druha priamka a stale su ovce
// neleziace na priamke, uz vrati zapornu odpoved.
bool over_na_priamke(int a,int b,bool prva)
{
napriamke[a] = napriamke[b] = true;
// toto je priamka urcena ovcami a,b
ovca vektor = {stado[b].x-stado[a].x,stado[b].y-stado[a].y};
vektor = zakladny_tvar(vektor);
// sem dame vsetky ovce ktore nelezia na ziadnej skusanej priamke
vector<int> zle;
for(int i=0;i<n;++i)
{
if(i==a || i==b) continue;
ovca tmp = {stado[i].x-stado[a].x,stado[i].y-stado[a].y};
tmp = zakladny_tvar(tmp);
// ak je ovca cislo i na rovnakej priamke ako a,b oznacime ju
// inak, ak nie je oznacena ako na priamke, ju pridame do zoznamu oviec ktore niesu na ziadnej skusanej priamke
if(vektor.x == tmp.x && vektor.y == tmp.y)
napriamke[i] = true;
else if(!napriamke[i]) zle.push_back(i);
}
// ak uz skusame druhu priamku, musime mat 0 zlych oviec
if(!prva) return zle.empty();
// ak mame najviac 2 ovce, nasli sme riesenie
if(zle.size()<=2) return true;
// skusime overit ci vsekty zvysne ovce lezia na priamke urcenej prvymi dvoma zlymi ovcami
return over_na_priamke(zle[0],zle[1],false);
}
int main()
{
cin >> n;
if(n<=4)
{
cout << "ANO\n";
return 0;
}
stado.resize(n);
napriamke.resize(n);
for(int i=0;i<n;++i)
cin >> stado[i].x >> stado[i].y;
// budeme skusat priamku urcenu ovcami i a j.
for(int i=0;i<2;++i)
{
for(int j=i+1;j<3;++j)
{
// kazdu ovcu oznacime ako neleziacu na priamke
for(int k=0;k<n;++k)
napriamke[k] = false;
// ak najdeme riesenie, hned povieme ano a skoncime
if(over_na_priamke(i,j,true))
{
cout << "ANO\n";
return 0;
}
}
}
// ani raz sme nenasli riesenie, povieme nie
cout << "NIE\n";
return 0;
}
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.