Zadanie
Istej nemenovanej firme sa ako prvej podarilo vyvinúť teleportujúce zariadenie. To vykonáva takú činnosť, že vezme objekt na jednej stanici, rozseká ho na atómy, tie pošle na druhú stanicu, a tam z atómov objekt napäť poskladá. Už má v krajine nainštalovaných viacero takýchto párov teleportov, a každý pár umožňuje rýchlo cestovať zo zdrojového mesta do cieľového mesta (ale nie opačným smerom).
Človek by očakával, že za použitie teleportu je potrebné zaplatiť, tak ako pri iných dopravných prostriedkoch. Pri niektorých pároch teleportov sa ale firma rozhodla, že za ich použitie cestujúcemu zaplatí, aby tak podporila používanie teleportov a aby ľudia prekonali počiatočnú nedôveru v tento spôsob dopravy.1
Takto ľahko zarábať peniaze, no kto by to neodmietol? Buj teda určite nie. Má to ale jedno obmedzenie – podľa firmy je za jeden deň bezpečné použiť teleport iba \(k\)-krát.
Aby si Buj vedel svoju cestu naplánovať, potrebuje pre každú dvojicu miest zistiť, koľko najviac peňazí môže zarobiť (alebo koľko najmenej musí zaplatiť), ak sa chce dostať z prvého mesta do druhého použitím najviac \(k\) teleportov.
Úloha
Zadaný je orientovaný graf s ohodnotenými hranami, a kladné celé číslo \(k\). Pre každú usporiadanú dvojicu vrcholov zistite, či existuje sled dĺžky najviac \(k\) začínajúci v prvom vrchole a končiaci v druhom. Ak áno, tak zistite, aký najväčší súčet hodnôt hrán môže mať taký sled.
Formát vstupu
Na prvom riadku vstupu sú tri celé čísla: počet vrcholov grafu \(n\) (\(\geq 1\)), počet hrán grafu \(m\) (\(\geq 0\)) a číslo \(k\) (\(\geq 0\)) s rovnakým významom, ako je uvedené vyššie.
Nasleduje \(m\) riadkov, každý z nich popisuje jednu hranu grafu. Pozostáva z troch celých čísel \(a, b, h\) oddelených jednou medzerou, hovoriacich, že v grafe sa nachádza hrana z vrcholu \(a\) do \(b\) s hodnotou \(h\). Platí \(1 \leq a, b \leq n\) (\(a\) a \(b\) môžu byť rovnaké), \(|h| \leq 10^9\), a pre každé dva (nie nutne rôzne) vrcholy platí, že existuje najviac jedna hrana vedúca z prvého vrcholu do druhého.
Obmedzenia
| Sada | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \(n \leq\) | \(10\) | \(17\) | \(31\) | \(56\) | \(100\) |
| \(k \leq\) | \(10\) | \(10^3\) | \(10^5\) | \(10^7\) | \(10^9\) |
Formát výstupu
Vypíšte tabuľku \(n \times n\) (teda \(n\) riadkov, a v každom riadku \(n\) políčok tabuľky oddelených medzerou). V \(i\)-tom riadku na \(j\)-tom políčku zľava nech je X, ak neexistuje sled z \(i\) do \(j\) dlhý najviac \(k\). Ak existuje, tak nech v tom políčku je číslo vyjadrujúce najväčší súčet hodnôt hrán spomedzi vyhovujúcich sledov.
Tieto čísla môžu byť veľké, preto tam, kde je to treba, použite \(64\)-bitový číselný typ (long long).
Príklady
Input:
4 4 3
1 2 -1
2 3 -1
3 4 -1
4 3 3Output:
0 -1 -2 -3
X 0 1 -2
X X 2 1
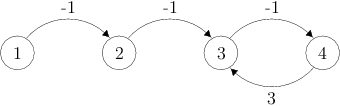
X X 5 2Graf z príkladu vyzerá takto:
Existujú ale konšpiračné teórie, podľa ktorých iba zháňajú lacných testerov, alebo dokonca ovládnu myseľ používateľov tým, že ich mozog poskladajú inak.↩
Krátka reklama pre skúsených: Táto úloha vám dá úplne nový pohľad na štandardný algoritmus umocňovania matice. Zistíte, že sa dajú umocňovať matice s operáciami inými ako \(+\) a \(\cdot\).
Ako to súvisí s úlohou? Čítajte.
Pomalé riešenie
Predstavme si, že už máme tabuľku najhodnotnejších sledov dĺžky \(k\). Pomocou nasledovnej úvahy z nej získame tabuľku najhodnotnejších sledov dĺžky \(k + 1\): každý sled dĺžky \(k + 1\) začínajúci v \(A\) a končiaci v \(B\) vieme získať ako kombináciu nejakého sledu dĺžky \(k\) začínajúceho v \(A\) a končiaceho v nejakom vrchole \(C\), a hrany z \(C\) do \(B\).
Takže by sa nám stačilo pozerať na všetky takéto kombinácie, a spomedzi nich zobrať tú najhodnotnejšiu. Týchto kombinácii je veľa, avšak si uvedomme, že keď hľadáme najhodnotnejší sled dĺžky \(k + 1\) (z \(A\) do \(B\)), stačí sa pozerať iba na najhodnotnejšie sledy dĺžky \(k\) (začínajúce v \(A\)). A o týchto máme informáciu v aktuálnej tabuľke. Postupne teda vyskúšame každý vrchol \(C\) ako predposledný vrchol sledu.
Dostávame tak algoritmus s časovou zložitosťou \(O(n^3 \cdot k)\).
Mocnenie
Sled dĺžky \(k\) nemusíme zostrojovať ako sled dĺžky \(k - 1\) plus sled dĺžky \(1\). Môžeme ho zostrojiť ako sled dĺžky \(k - a\) plus sled dĺžky \(a\) pre ľubovoľné \(a\).
Takže ak \(k = 2 \cdot k'\), stačí nám rekurzívne vypočítať tabuľku najhodnotnejších sledov dĺžky \(k'\), a tú následne skombinovať samú so sebou. Ak \(k = 2 \cdot k' + 1\), tak postupujeme tak, že vypočítame tabuľku najhodnotnejších sledov dĺžky \(k - 1\), a tú skombinujeme s tabuľkou hrán (ako pri pomalom riešení).
Výsledný algoritmus má rovnakú časovú zložitosť, ako umocňovanie matíc, teda \(O(n^3 \cdot \log k)\). V podstate totiž umocňujeme maticu s operáciami \(min, +\). Záujemcovia sa môžu zamyslieť nad všeobecným kritériom, ktoré by mali spĺňať dve operácie \(\oplus, \otimes\) na to, aby pre ne “fungovalo” násobenie matíc.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.