Zadanie
Bol raz jeden algoritmus, ktorého každodennou prácou bolo hľadanie najdlhšej cesty v strome s vrcholmi od \(1\) po \(n\). Jeho metóda bola nasledovná:
Strom si zakoreníme za vrchol s najmenším číslom.
Pre každého syna koreňa nájdeme najdlhšiu cestu, ktorej jeden koniec je samotný syn, a druhý koniec je v jeho podstrome. To spravíme obyčajným prehľadávaním do šírky.
Vyberieme dvoch synov s najdlhšími cestami. Keď tieto dve cesty prepojíme cez koreň, dostaneme najdlhšiu cestu prechádzajúcu koreňom.
Ešte sme ale nebrali do úvahy cesty, ktoré koreňom vôbec neprechádzajú. Každá taká cesta ale leží celá v podstrome niektorého syna. Stačí preto rekurzívne vyriešiť tieto podstromy – zakoreníme ich, spočítame pre synov koreňa najdlhšie cesty, …
Kolega programátor mu poradil, že ak by za koreň vždy zvolil centroid1 (pod)stromu, tak by mal oveľa viac voľného času, lebo by vraj bežal v čase \(O(n \log {n})\) namiesto \(O(n^2)\).
Algoritmus sa nad tým zamyslel, a všimol si, že jeden strom môže mať viac ako jeden centroid. V takých prípadoch by sa musel rozhodnúť, ktorý z centroidov vybrať. S tým sa mu ale nechce otravovať. Zaujíma ho preto, koľko stromov s \(n\) vrcholmi je takých, že práca na ňom podľa nového postupu bude čisto manuálna, a nebude musieť počas nej robiť žiadne rozhodnutia.
Úloha
Strom je ľahký, ak má práve jeden centroid, a jeho odobratím sa strom rozpadne na niekoľko ľahkých stromov. Pre zadaný počet vrcholov \(n\) zistite, koľko rôznych stromov s \(n\) vrcholmi je ľahkých. (Dva stromy považujeme za rôzne, ak existujú vrcholy \(u, v\), ktoré sú hranou spojené v prvom strome, ale nie v druhom.) Toto číslo môže byť veľké, vypíšte preto jeho zvyšok po delení prvočíslom \(p\).
Formát vstupu
Na jedinom riadku vstupu sú dve celé čísla \(n, p\) oddelené medzerou. \(n\) udáva počet vrcholov a \(p\) je prvočíslo, po delení ktorým berieme zvyšok.
Je päť testovacích sád. Vo všetkých platí \(1 \leq n \leq 3\,000\), a \(n < p \leq 10^9\). Pre jednotlivé sady máme nasledovné obmedzenia:
| číslo sady | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \(n \leq\) | \(9\) | \(100\) | \(500\) | \(1\,000\) | \(3\,000\) |
Formát výstupu
Na jediný riadok výstupu vypíšte jedno celé číslo z \(\lbrace 0, 1, \ldots, p - 1 \rbrace\) – počet vyhovujúcich stromov s \(n\) vrcholmi, modulo \(p\).
Príklady
Input:
2 103Output:
0Pre \(n = 2\) existuje iba jeden strom:
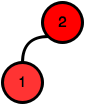
Tento strom nevyhovuje, nakoľko v prvom kroku môžeme za koreň zvoliť aj vrchol \(1\), aj \(2\).
Input:
4 103Output:
4Pre \(n = 4\) máme tieto štyri vyhovujúce stromy:
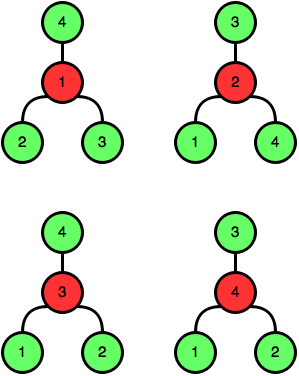
Príklad nevyhovujúceho stromu je
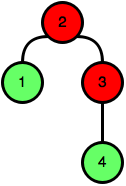
nakoľko môžeme v prvom kroku zvoliť za koreň \(2\) aj \(3\).
taký vrchol v strome, ktorého každý syn má podstrom obsahujúci nanajvýš polovicu všetkých vrcholov↩
Ukážeme si dve riešenia, prvé bežiace v čase \(O(n^2 \log n)\) (za ktoré sa dalo získať \(12\) až \(20\) bodov) a druhé \(O(n^2)\) (za plných \(20\) bodov). Nie je to ale tak, že by to rýchlejšie “budovalo” na tom pomalšom, oplatí sa preto prečítať si obe riešenia.
Úvaha na začiatok
Zoberme si ľubovoľný strom a niektorý jeho vrchol \(v\) taký, že jeho odobratím sa strom rozpadne na podstromy veľkosti nanajvýš \(\frac{n}{2}\). Potom ľahko vidno, že \(v\) je jeho jediný centroid práve vtedy, keď každý z tých podstromov má veľkosť ostro menšiu ako \(\frac{n}{2}\).
Označme počet ľahkých stromov s \(n\) vrcholmi ako \(f(n)\). Z vyššie uvedeného vyplýva, že \(f(n) = n \cdot nieco(n)\).
\(nieco(n)\) je vlastne počet rozdelení \(a = n - 1\) vrcholov do niekoľkých častí, pričom každá z nich je ľahký strom s najviac \(b = \lfloor\frac{n - 1}{2}\rfloor\) vrcholmi, a jeden vrchol z každého stromu je spojený s centroidom. Pre všeobecné \(a\) a \(b\) to budeme označovať \(rozdel(a, b)\).
Ak chceme vypočítať \(rozdel(a, b)\), tak sa oplatí zamyslieť nad tým, ako by sme vedeli systematicky riešiť problém “máš \(a\) vrcholov, postav z nich niekoľko ľahkých stromov veľkosti najviac \(b\)”.
Riešenie 0 “za nula bodov”
Môžeme napríklad stavať stromy postupne. Pri stavaní jedného stromu musíme určiť jeho veľkosť \(k\), potom množinu jeho vrcholov, a jeho tvar (teda ako sú vrcholy v ňom pospájané). Nakoniec ho musíme niektorým vrcholom spojiť s centroidom. O ostatné stromy sa postaráme tak, že vlastne riešime ten istý problém: “máš \(a - k\) vrcholov, postav z nich niekoľko ľahkých stromov veľkosti najviac \(b\)”.
Ak sme si zvolili veľkosť \(k\), tak na množinu jeho vrcholov máme \({a \choose k}\) možností, na jeho tvar je \(f(k)\) možností, a vrchol spojený s centroidom vieme vybrať \(k\) spôsobmi. Teda to vyzerá tak, že
\[rozdel(a, b) = \sum_{k = 1}^{b} {a \choose k} \cdot f(k) \cdot k \cdot rozdel(a - k, b)\]
Šikovný čitateľ si ale isto všimol, že horeuvedeným postupom vieme niektoré rozdelenia dosiahnúť viacero spôsobmi, a teda neplatí, že počet rôznych postupov je rovný \(rozdel(a, b)\). Problém je vlastne v tom, že si môžeme vybrať poradie, v akom budeme stromy zostrojovať, pričom ale výsledné rozdelenie nezávisí od tohto poradia.
Riešenie 1 “od najväčšieho po najmenší”
To môžeme vyriešiť tak, že budeme stromy zostrojovať od najväčšieho po najmenší, pričom v jednom kroku zostrojíme naraz všetky najväčšie (ešte nepostavené) stromy. Pribudne nám teda ešte jeden parameter – počet stromov s veľkosťou \(b\), ktorý môže byť od \(0\) po \(\lfloor\frac{a}{b}\rfloor\).
Ak sme si zvolili počet stromov \(s\), tak množiny vrcholov vieme vybrať \[\frac{\prod_{i = 0}^{s - 1} {{a - i \cdot b} \choose b}}{s!}\] spôsobmi. Na ich tvary máme \(f(b)^s\) možností, a vrcholy spojené s centroidom vieme vybrať \(b^s\) spôsobmi. Dokopy
\[rozdel(a, b) = \sum_{s = 0}^{\lfloor\frac{a}{b}\rfloor} \frac{\prod_{i = 0}^{s - 1} {{a - ib} \choose b}}{s!} \cdot f(b)^s \cdot b^s \cdot rozdel(a - sb, b - 1)\]
Pozrime sa teraz na časovú zložitosť. Všetky kombinačné čísla a faktoriály modulo \(p\) si vieme dopredu predrátať, čiže to je konštanta. Na výpočet \(rozdel(a, b)\) potrebujeme rádovo \(\frac{a}{b}\) sčítancov, a každý z nich vieme spočítať v konštantnom čase. Pre pevné \(a\) nás zaujímajú \(b\) od \(1\) po \(\lfloor\frac{a}{2}\rfloor\), a stojí nás to rádovo \(\frac{a}{1} + \frac{a}{2} + \ldots + \frac{a}{\lfloor\frac{a}{2}\rfloor} \approx a \log a\). Keď to sčítame cez všetky \(a\) (od \(1\) po \(n\)), dostaneme časovú zložitosť \(O(n^2 \log n)\).
Riešenie 2 “to sú mi triky”
V tomto riešení nebudeme počítať \(rozdel(a, b)\) všeobecne, ale len pre tú hodnotu, ktorá nás najviac zaujíma: pre \(b = \lfloor\frac{a}{2}\rfloor\).
Zamyslime sa najprv nad tým, koľkými spôsobmi vieme \(a\) vrcholov rozdeliť do niekoľko ľahkých stromov a každý z nich spojiť jednou hranou s centroidom, ale bez obmedzenia na veľkosť stromu. V podstate nás teda zaujíma \(rozdel(a, a)\).
Túto hodnotu budeme počítať podobným spôsobom, ako v riešení za nula bodov. Jednoznačnosť zaručíme tak, že v každom kroku zostrojíme strom obsahujúci vrchol s najmenším číslom. Dostávame tak mierne odlišný vzťah
\[rozdel(a, a) = \sum_{k = 1}^{a} {a \choose {k - 1}} \cdot f(k) \cdot k \cdot rozdel(a - k, a - k)\]
(Všimnite si, že pri voľbe množiny vrcholov vyberáme o \(1\) vrchol menej, a preto tam je \({a \choose {k - 1}}\) namiesto \({a \choose k}\).)
Samozrejme, nemôžeme túto hodnotu prehlásiť za \(\frac{f(a + 1)}{a + 1}\) – zarátali sme tam totiž aj rozdelenia, v ktorých existuje strom s viac ako \(\lfloor\frac{a}{2}\rfloor\) vrcholmi.
Koľko takých zlých stromov ale môže existovať? Ak by boli dva, tak by sme mali aspoň \(2 \cdot (\lfloor\frac{a}{2}\rfloor + 1)\) vrcholov okrem centroidu, čo je väčšie než \(2 \cdot \frac{a}{2} = a\), skutočný počet vrcholov okrem centroidu. To by bol spor. Takže zlý strom je vždy najviac jeden.
To ale znamená, že všetky zlé možnosti vieme zostrojiť tak, že najprv zostrojíme zlý strom, a potom všetky ostatné (pri ktorých už nedbáme na obmedzenia veľkosti). Týchto možností teda je
\[zle(a) = \sum_{z = \lceil\frac{a}{2}\rceil}^{a} {a \choose z} \cdot f(z) \cdot z \cdot rozdel(a - z, a - z)\]
A máme tak
\[f(a + 1) = (a + 1) \cdot rozdel\left(a, \left\lfloor\frac{a}{2}\right\rfloor\right) = (a + 1) \cdot (rozdel(a, a) - zle(a))\]
Toto riešenie má časovú zložitosť \(O(n^2)\), lebo počítame iba \(n\) hodnôt \(rozdel(1, 1), \ldots, rozdel(n, n)\), a každú z nich vypočítame v \(O(n)\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.