Zadanie
Na pondelňajší krúžok matematiky nikto okrem vás a učiteľky neprišiel, lebo všetci sú na lyžiarskom zájazde. Učiteľka sa preto rozhodla hodinu spraviť trochu interaktívnejšou, nakoľko sa nemusí venovať desiatim študentom naraz.
Úloha
Na začiatku si učiteľka tajne zvolí dve celé čísla: modulus \(m\) (\(1 \leq m\)) a stav \(x_0\) (\(0 \leq x_0 < m\)). Vašou úlohou je tieto dve čísla uhádnuť pomocou niekoľkých otázok. Učiteľka vám na začiatku oznámi, že modulus je najviac \(n\), a že sa môžete spýtať najviac \(q\) otázok.
Každá otázka vyzerá nasledovne: Vy si zvolíte jedno celé číslo \(a\) (\(1 \leq a \leq n\)). Učiteľka zoberie aktuálny stav \(x_i\) a vypočíta z neho nový stav \(x_{i+1}\) použitím nasledovného vzorca: \(x_{i+1} = (x_i + a) \bmod m\). Vám však nič z toho neukáže. Jediné, čo vám na konci oznámi, je, či je nový stav menší, rovnaký, alebo väčší ako predchádzajúci stav.
Kedykoľvek môžete skúsiť uhádnuť \(m\) a \(x_0\), najneskôr ale po \(q\) otázkach. Môžete hádať iba raz.
Formát vstupu
Na začiatku dostanete celé číslo \(t\): koľkokrát sa s vami bude učiteľka hrať (ak ju v predchádzajúcich hrách nesklamete).
Na začiatku každej hry dostanete celé čísla \(n\) a \(q\). Po každej vašej otázke dostanete na samostatný riadok odpoveď: > ak sa stav zväčšil, = ak je rovnaký, a < ak sa zmenšil.
Formát výstupu
Každú otázku píšte do samostatného riadku, a musí pozostávať z jedného celého čísla \(a\) (\(1 \leq a \leq n\)). Váš tip tiež vypíšte do samostatného riadku v tvare 0 m x0.
Obmedzenia
Je päť testovacích sád, s nasledujúcimi obmedzeniami:
| Sada | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \(t\) | \(2\,016\) | \(1\,000\) | \(200\) | \(100\) | \(200\) |
| \(n\) | \(63\) | \(250\) | \(10\,000\) | \(10^9\) | \(10^{18}\) |
| \(q\) | \(126\) | \(251\) | \(2\,300\) | \(2\,600\) | \(1\,200\) |
Poznámky
Nezabudnite po každej vašej otázke alebo tipe flush-núť výstup, aby sa hneď odoslal testovaču. (cout.flush() v C++, fflush(stdio) v C, sys.stdout.flush() pre Python, a System.out.flush() v Jave.)
Keď váš program zo vstupu prečíta EOF (čiže keď sa mu nepodarí načítať nejaký údaj), váš program by mal hneď skončiť. Toto môže nastať napríklad vtedy, keď ste v práve skončenej hre zle odpovedali. Teraz čakáte ďalšie \(n\) a \(q\), na vstupe vám však už žiadne údaje neprídu.
Ak bude váš program naďalej bežať a pokúšať sa komunikovať, môže sa stať, že namiesto WA dostanete EXC, TLE, alebo iné zveriny.
Príklady
Input:
2
2 9
<
>
<
1 9
Output:
1
1
1
0 2 1
0 1 0Skúsme na začiatok iba vyriešiť úlohu, nezáleží na tom, ako efektívne. Keď budeme klásť iba otázky \(1\), budeme podľa odpovede vedieť presne povedať, čo sa stalo:
- Ak sme dostali
>, tak sa stav zvýšil o \(1\). - Ak sme dostali čokoľvek iné, tak sme pretiekli – stav dosiahol po pripočítaní \(1\) hodnotu \(m\), a keď sme zobrali jeho zvyšok po delení \(m\), dostali sme stav \(0\).
Nápad je taký, že ak by sme začínali v stave \(0\), budeme sa pýtať stále otázky \(1\), až kým nedostaneme = alebo <. Počet položených otázok je potom presne \(m\). Do stavu \(0\) sa ale vieme dostať rovnakým spôsobom – pýtaním sa \(1\) dovtedy, kým nedostaneme niečo iné ako >. Máme tak algoritmus, ktorý sa opýta najviac \(2n\) otázok.

Dolný odhad
Všimnime si, že ak sa \(k\)-krát spýtame otázku \(1\), a na každú dostaneme odpoveď >, tak určite platí \(m \geq k + 1\). Toto vieme využiť na zrýchlenie predchádzajúceho algoritmu:
Ak v prvej časti algoritmu použijeme \(k\) otázok, tak sa v druhej časti nemusíme na začiatku \((k - 1)\)-krát spýtať \(1\). Vieme, že na každú z tých otázok dostaneme > – nedostaneme žiadnu informáciu. Namiesto toho, aby sme sa \(k\)-krát spýtali \(1\), sa raz spýtajme \(k\). Máme tak algoritmus pýtajúci sa najviac \(n + 1\) otázok.

Načo nám je dolný odhad?
Pozrime sa na to, čo nám hovorí odpoveď na otázku \(a\). Dostaneme > ak \(x + a < m\), v opačnom prípade môžeme dostať >, = aj <. Takže vo všeobecnosti to nevyzerá byť veľmi užitočné. Vieme, že ak dostaneme = alebo <, tak sme pretiekli. Ak sme ale dostali >, tak sme mohli ale nemuseli pretiecť.
Ako uvidíme, pomocou dolného odhadu budeme vedieť klásť také otázky \(a\), že budeme vedieť povedať, či sme pretiekli alebo nie.
Jeden špeciálny prípad sme už videli, a to \(a = 1\). (Zrejme \(m \geq 1\), teda \(1\) naozaj je dolný odhad na \(m\).) Pre nový stav \(x + 1 \mod m\) totiž platí \(x < x + 1 \leq x + m\), a ak sme pretiekli, tak máme \(x + 1 \geq m\). Dokopy \(m \leq x + 1 \leq x + m\), takže nový stav je rovný \(x + 1 - m\), čo je nanajvýš \(x\). Nemôžeme preto dostať pri pretečení >.
Namiesto \(a = 1\) sme mohli ale uvažovať ľubovoľné \(a \leq m\), a úvahy by prešli rovnako. Voľbu takýchto \(a\) nám umožňuje práve dolný odhad na \(m\): ak \(l\) je dolný odhad na \(m\), tak môžeme bezpečne zvoliť \(a \leq l\).
Načo nám je schopnosť rozlíšiť pretečenie?
Ak sme pretiekli po položení otázky \(a\), vieme, že sme v stave nanajvýš \(a - 1\). Keď sa ďalej spýtame otázky so súčtom \(s\), tak sa náš stav zvýši nanajvýš o toľko, budeme teda v stave nanajvýš \(\leq s + a - 1\). Takže za určitých okolností vieme zhora obmedziť náš stav.
Predpokladajme ďalej, že sme sa spýtali otázky so súčtom \(s\), pričom sme pretiekli iba pri poslednej otázke. Ak by \(m > s + a - 1\), tak by sme nepretiekli – tento prípad preto nemohol nastať, a preto \(m \leq s + a - 1\). Takže schopnosť rozlíšiť pretečenie nám umožňuje zhora odhadnúť \(m\).
Takisto nám ale umožňuje \(m\) odhadnúť zdola. Keď sa spýtame otázky so súčtom \(s\), a pri ani jednej nepretečieme, tak nutne \(m > s\).
Zistime modulus
Videli sme, že ak vieme rozlíšiť pretečenie, tak vieme pomocou otázok zhora aj zdola obmedzovať \(m\). To bude hlavná myšlienka nášho algoritmu.
Nech sme na začiatku v niektorom zo stavov \(\lbrace 0, 1, \ldots, a - 1 \rbrace\), a nech \(l < m \leq r\): máme teda dolné aj horné obmedzenie na \(m\). (Napríklad \(l = 0\) a \(r = n\).)
Budeme postupovať v kolách. V každom kole je naším cieľom zmenšiť interval, v ktorom je \(m\), dvakrát – ak by sme to dokázali, počet kôl bude len \(O(\log{n})\). A ak by sme sa v každom kole spýtali iba konštantne veľa otázok, tak máme vyhraté.
V každom kole sa budeme pýtať dokola nejakú otázku \(b\), až kým nepretečieme. Ak sme sa do pretečenia spýtali \(k\) otázok, tak máme dolný odhad \(m > kb\), a horný odhad \(m \leq (k + 1)b + a - 1\). Oklieštime tak \(m\) v intervale dĺžky najviac \(b + a - 1\).
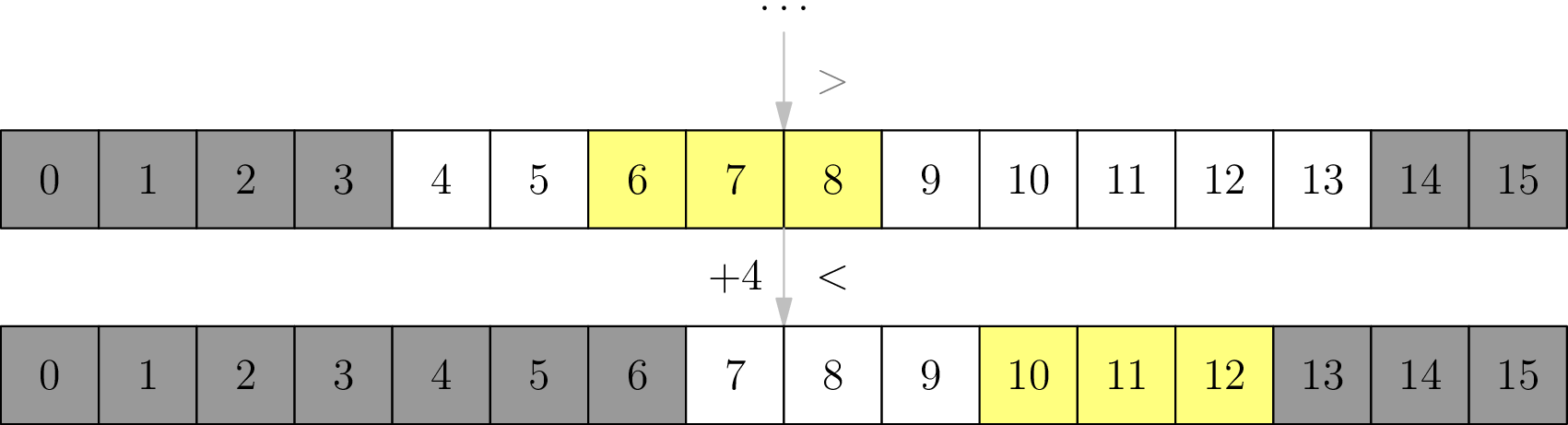
Všimnime si ale, že v každom kole spravíme aspoň \(\left\lceil\frac{l - a + 1}{b}\right\rceil\) otázok – čo nie je zhora obmedzené konštantou, nakoľko \(l\) je rádovo \(n\). Tento problém ale vyriešime známym trikom: rovno sa na začiatku spýtame \(l - a + 1\), čím sa “presunieme tesne pred \(l\)”. (Konkrétne náš stav bude v \(\lbrace l - a + 1, \ldots, l \rbrace\).) Teraz sa v jednom kole spýtame rádovo \(\left(\frac{r - l}{b}\right)\)-krát, takže chceme, aby \(b\) bolo rádovo \(r - l\). Napríklad nech \(b = \left\lceil\frac{r - l}{4}\right\rceil\).
Náš interval sa má zmenšiť dvakrát, teda má platiť \(b + a - 1 \leq \left\lceil\frac{r - l}{2}\right\rceil\). Chceli by sme preto, aby platilo \(a \leq \left\lceil\frac{r - l}{4}\right\rceil\). To vieme zaručiť tak, že pred každým kolom budeme mať predkolo, v ktorom sa budeme pýtať \(\left\lceil\frac{r - l}{4}\right\rceil\) dovtedy, dokým nepretečieme. Po pretečení budeme v stave \(\leq \left\lceil\frac{r - l}{4}\right\rceil - 1\), a teda \(a = \left\lceil\frac{r - l}{4}\right\rceil\). Môže sa ale stať, že sa v predkole spýtame priveľa (nie konštantne veľa) otázok, čo vyriešime tak, že sa na začiatku predkola presunieme tesne pred \(l\).
Zhrnutie
Našli sme teda vhodné konštanty \(a, b\) také, že sa náš algoritmus spýta najviac \(O(\log{n})\) otázok a zistí \(m\). Pri tom sme využívali schopnosť rozlíšiť pretečenie – ako sme ale videli, vo všeobecnosti to nevieme robiť pre každú otázku. V skutočnosti sa algoritmus smie pýtať len otázky \(\leq l\) (kde \(l\) je najlepšie dolné ohraničenie \(m\), o ktorom aktuálne vie). Na to, aby uspel, potrebujeme nájsť \(l < m \leq r\) také, že \(r - l\) je rádovo nanajvýš \(l\). Túto časť prenechávame vám – ak ste sa ale dočítali až sem, tak by ste s tým nemali mať problém.
Hľadanie pôvodného stavu
Po tom, čo nájdeme \(m\), nám stačí zistiť aktuálny stav. Môžeme si totiž pamätať všetky položené otázky, a keď zistíme aktuálny stav, jednoducho dopočítame pôvodný stav \(x_0\).
Ako nájsť aktuálny stav? No predsa binárnym vyhľadávaním. V ňom sa potrebujeme vedieť pýtať “je \(x\) aspoň \(b\)?” To vieme v našej úlohe zistiť tak, že položíme otázku \(m - b\). Ak dostaneme >, tak \(x < b\), v opačnom prípade \(x \geq b\). Následne sa vrátime k predchádzajúcemu stavu tým, že sa spýtame \(b\) (a odpoveď ignorujeme).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.