7. Obézni brankári vzorové riešenie

3 47

13

7 1000

29

Táto úloha na prvý pohľad vyzerala ako nejaká komplikovaná kombinátorika. V skutočnosti to tak vôbec nebolo, išlo len o efektívne spočítanie všetkých možností vyplnenia obdĺžnika. Poďme sa najprv pozrieť na spôsob, ako tieto možnosti spočítať hrubou silou. (Odporúčam nepreskakovať riešenie hrubou silou, sú v ňom veľmi dôležité myšlienky potrebné pre pochopenie vzorového riešenia.)

Hrubá sila – vypĺňanie po jednotlivých políčkach

Poviete si: “Poďme vygenerovať všetky možnosti!”, otázka však je ako. Jeden zo spôsobov by mohol byť, že si zoberieme prázdnu bránku a budeme do nej postupne všetkými možnosťami umiestňovať štvorce. Vždy, keď je bránka plná, započítame toto rozloženie do výsledku. Musíme ale nájsť taký spôsob vytvárania (prehľadávania) všetkých rozložení, aby sme každé rozloženie navštívili len raz.

Jeden zo spôsobov by mohol byť taký, že postupne prechádzame políčka bránky zhora dole, zľava doprava. Ak nájdeme nevyplnené políčko, skúsime sem vložiť štvorce všetkých možných veľkostí tak, aby na tomto políčku ležali ľavým horným rohom (vždy skúsime vložiť 1 štvorec a potom rekurzívne zavoláme funkciu, čo vyplní zvyšok bránky). Takto vždy zapĺňame políčka len smerom dole a doprava od našej pozície a všetky políčka smerom hore a doľava od nás sú už určite vyplnené. Pri vytváraní rozložení nevytvoríme žiadne viackrát (lebo každé dve sa líšia veľkosťou brankára aspoň na jednom políčku – ľavom hornom rohu nejakého brankára) a takisto vytvoríme každé.

Toto riešenie sa ľahko vymyslí, aj implementuje, no navštívi všetky rozloženia, ktorých je exponenciálne veľa.

Hrubá sila – vypĺňanie po stĺpcoch

Čo ak by sme mali už vygenerované všetky bránky veľkosti \(4 \times n\)? Dokážeme z týchto bránok vygenerovať všetky bránky veľkosti \(4 \times (n + 1)\)? Odpoveď znie, áno, a budeme to robiť nasledovne. Predstavme si, že máme už vygenerované konkrétne rozloženie veľkosti \(4 \times n\):

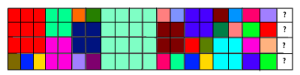
Oblasť jednej farby je jeden brankár. Otázniky v poslednom stĺpci reprezentujú nový stĺpec, ktorý chceme pridať (teraz budeme pridávať brankárov do stĺpca tak, aby boli zarovnaní podľa pravého kraja – teda aby sme presne vyplnili obdĺžnik \(4 \times (n + 1)\)). Je jasné, že v pôvodnom rozložení musíme aj niečo zmeniť, inak by sme mohli predsa pridať len samých jednotkových brankárov. Avšak, ak budeme meniť ľubovoľne, môžme dôjsť k problému generovania rovnakého rozloženia viackrát.

Do stĺpca s otáznikmi umiestníme ľubovoľne veľkých brankárov, ktorí sa tam zmestia. V pôvodnom rozložení budú však môcť prekryť (a teda nahradiť) len jednotkových brankárov. Na našom obrázku máme napravo celkom pekné množstvo jednotkových brankárov. Jediného brankára, ktorého si nemôžeme dovoliť do stĺpca s otáznikmi umiestniť je brankár veľkosti \(4 \times 4\), pretože ten by musel prekryť tyrkysového brankára \(2 \times 2\) a vieme, že takého prekryť nemôžeme.

Vždy je najviac osem možností, ako umiestniť brankárov do stĺpca s otáznikmi (odporúčam si ich vypísať na papier), pre každú bránku veľkosti \(4 \times n\) je teda celkom ľahko možné vygenerovať najviac \(8\) bránok veľkosti \(4 \times (n + 1)\).

Ukážme si ešte, že takýmto spôsobom vygenerujeme každé rozloženie a žiadne nevygenerujeme dvakrát. Zoberme si nejaké konkrétne rozloženie \(4 \times n\) a každého brankára, ktorý sa dotýka pravého okraja bránky nahraďme jednotkovými brankármi a potom odstráňme posledný stĺpec. Týmto spôsobom dostaneme rozloženie veľkosti \(4 \times (n - 1)\), z ktorého bolo naše rozloženie veľkosti \(4 \times n\) vygenerované. Vidíme teda, že každé rozloženie \(4 \times n\) vieme vygenerovať, ak už máme vygenerované všetky rozloženia veľkosti \(4 \times (n - 1)\). Každé dve rozloženia veľkosti \(4 \times n\) sa budú líšiť buď v poslednom stĺpci, alebo v rozloženiach \(4 \times (n - 1)\), z ktorých boli vygenerované.

Budeme si teda postupne generovať rozloženia pre stále dlhšiu a dlhšiu bránku, až sa nakoniec dostaneme po našu cieľovú šírku bránky. Toto riešenie je však pomerne pomalé. Z každej bránky \(4 \times n\) vygenerujeme prinajhoršom až \(8\) bránok veľkosti \(4 \times (n + 1)\) a tak časová zložitosť môže byť až exponenciálna (aj pamäťová, ak si udržiavame všetky doteraz vygenerované rozloženia).

Poďme sa teda pozrieť na to, ako toto riešenie výrazne zefektívniť. (Pre porozumenie ďalším riešeniam je však veľmi dôležité v prvom rade porozumieť aktuálnemu.)

Brankári si udržujú líniu – lineárne riešenie

V predchádzajúcom riešení môžeme spraviť nasledujúce pozorovanie: to, akých brankárov môžeme pridať do posledného stĺpca s otáznikmi závisí len a len od počtu jednotkových brankárov úplne napravo v každom riadku. Napríklad, ak pravý okraj nejakej bránky vyzerá takto (prázdne políčka bez otáznikov znamenajú hocijakých nejednotkových brankárov):

tak tam vieme doplniť nejakých jednotkových, dvojkových a dole aj trojkového brankára.

Úplne všetky rozloženia, ktoré končia takto, sa dajú do otáznikov doplniť rovnakými spôsobmi. Koľko je spôsobov, ktorými môžu rozloženia končiť? Keďže to závisí len od počtu jednotkových brankárov úplne napravo v každom riadku, a záleží nám len na posledných troch (lebo ďalších už nezvládame prekryť), tak možností je \(4^4\) (štyri riadky a v každom \(0 - 3\) jednotkových brankárov).

Slabina predchádzajúceho riešenia hrubou silou bola, že sme si pamätali úplne všetky rozloženia, aj tie, ktoré sa končili rovnako. Pekným vylepšením teda bude, že namiesto toho si budeme pamätať len počet rozložení pre každé možné ukončenie. Tým sa nám zlepší priestorová zložitosť na konštantnú, časová sa však nezmení.

Na to musíme spraviť ešte jedno vylepšenie. Zaveďme si malú terminológiu: stavom budeme nazývať ľubovoľnú z tých \(256\) možností, ktorými môže končiť rozloženie. Čo ak by sme si pre každý stav dopredu vypočítali, na aké ďalšie stavy sa môže zmeniť doplnením stĺpca s otáznikmi? Predpočítať to je pomerne jednoduché. Všetky prechody medzi rozloženiami si môžeme uložiť do veľkej tabuľky \(256 \times 256\), kde \(j\)-te políčko v \(i\)-tom riadku bude určovať, koľkými spôsobmi sa dá dostať zo stavu číslo \(j\) do stavu číslo \(i\) (prečo nie naopak, z \(i\) do \(j\) uvidíme čoskoro). Nazvime si túto tabuľku \(M\). (Situáciu si môžete predstaviť aj tak, že vytvoríme graf, kde stavy sú vrcholy a prechody medzi stavmi sú orientované hrany. \(i\)-ty riadok tabuľky hovorí, z ktorých vrcholov (stavov) sa dá dostať do stavu \(i\) a číslo na pozícii \((i, j)\) hovorí koľko hrán vedie z \(j\) do \(i\).)

V ďalšom jednorozmernom poli veľkosti \(256\) si budeme pamätať počty rozložení pre každý z \(256\) stavov. Nazvime si toto pole \(u\). Na začiatku máme len jeden stav \((0, 0, 0, 0)\). Vždy, keď už máme spočítané počty stavov pre šírku bránky \(n\), tak pre šírku \(n + 1\) spočítame ľahko. Označme si nové pole počtov stavov ako \(v\). Toto pole vypočítame jednoducho ako \(v_i = \sum_{j=0}^{255} u_j \cdot M_{i,j}\). Inými slovami, počet nových rozložení v stave \(i\) vypočítame tak, že spočítame všetky možnosti, ako sa doňho vieme dostať zo starých rozložení. Keďže tie máme uložené, ako počty v jednotlivých stavoch a pre každý stav vieme podľa tabuľky \(M\), kam sa z neho vieme dostať, tak nám stačí vždy vynásobiť počet rozložení v každom stave \(j\) s počtom možností, ako sa z tohoto stavu dostať do stavu \(i\) a celé to sčítať.

Celkový výsledok bude súčet počtov rozložení vo všetkých stavoch.

Týmto spôsobom dostaneme pekné lineárne riešenie. Výpočet riešenia pre každú ďalšiu šírku nám zaberie len konštantný čas, keďže počet stavov je konštantný a nijako nezávisí od vstupu.

Znížme počet stavov

Riešenie je síce lineárne od veľkosti \(n\), no konštanta, ktorou \(n\) násobíme je \(\left(4^4\right)^2 = 256^2 = 65536\), teda toto riešenie je prakticky použiteľné pre \(n\) rádovo \(100\).

Ak si ale maticu \(M\) vypíšeme na výstup, zistíme, že je pomerne riedka. Inými slovami, veľa stavov je úplne nedosiahnuteľných. Ako sa týchto stavov zbaviť? Jedno z riešení by bolo spraviť prehľadávanie do šírky na grafe, ktorý matica reprezentuje a takým spôsobom nájsť všetky stavy dosiahnuteľné zo stavu \((0, 0, 0, 0)\).

Existuje však aj jednoduchšie riešenie. Každý riadok v matici \(M\) určuje spôsob, ako vypočítať nový stav z predchádzajúcich stavov. Pokiaľ je celý riadok v matici nulový, tak stav, ktorý reprezentuje tento riadok nikdy nenadobudne žiadne rozloženie. Takýto stav je nedosiahnuteľný. Odstránime teda všetky nulové riadky a im prislúchajúce stĺpce. Týmto spôsobom nám môžu vzniknúť ďalšie nulové riadky a teda odstránime aj tie a tiež im prislúchajúce stĺpce. Tento proces opakujeme, až kým sa v matici nenachádzajú žiadne nulové riadky. Takto sa nám obrovská matica \(256 \times 256\) zredukuje na celkom príjemnú maticu \(30 \times 30\), čiže naše riešenie vyrieši úlohu aj pre \(n\) rádovo \(10000\). Konštanty sú niekedy podstatné :)

Smer čierna matematika (ale vôbec nie až tak)

Máme lineárne riešenie, ale to zjavne nestačí, keďže šírka bránky môže dosahovať pomerne závratné hodnoty. Keď sa však pozrieme na to, čo vlastne robíme v našom lineárnom riešení, tak nie je to nič iné, ako násobenie vektora maticou! (V podstate, výpočet počtu nových rozložení zo starých pomocou tabuľky je tak častá matematická operácia, že ju ľudia dobre preskúmali a nazvali súčinom matíc. Použite Google a Wikipédiu, ak ste ešte o násobení dvoch matíc a o násobení vektora maticou nepočuli.)

Pozrime sa opäť na to, ako z poľa (vektora) \(u\) vypočítame pole (vektor) \(v\). Náš vzorec bol:

\[ v_i = \sum_{j=0}^{255} u_j \cdot M_{i,j} \]

Ale toto je predsa násobenie vektora maticou! Ľahko to prepíšeme na:

\[ v = M \cdot u \]

Takto vypočítame počty stavov v bránke o jedna väčšej. Čo ak chceme vypočítať počty stavov v bránke o \(2\) väčšej? Jednoducho:

\[ v = M \cdot M \cdot u \]

Tu sa nám začína rysovať celkom jednoduchý pattern. Ak chceme vypočítať počty stavov v bránke o \(n\) väčšej, tak to spravíme takto:

\[ v = M \cdot M \cdot \dots \cdot M \cdot v = M^n \cdot u \]

Hurá, tým sme sa naozaj posunuli ďalej, pretože matice vieme umocňovať v logaritmickom čase¹! Takýmto spôsobom sme dostali riešenie s časovou zložitosťou \(O(\log n)\) a pamäťovou \(O(1)\).

#include <iostream>
#include <vector>

using namespace std;

long long MOD;

// datova struktura reprezentujuca maticu a peknymi operaciami
// podporuje len stvorcove matice, ale tie nam v tejto ulohe stacia
struct matrix {
    int size;
    vector<vector<long long>> fields;

    matrix(int size) {
        this->size = size;
        fields = vector<vector<long long>>(size, vector<long long>(size, 0));
    }

    // vygeneruje nam diagonalnu (jednotkovu) maticu
    static matrix diagonal(int size) {
        matrix d(size);
        for (int k = 0; k < size; ++k) {
            d.fields[k][k] = 1;
        }
        return d;
    }

    // vynasobi dve matice v case O(n^3), kde n je velkost matice
    matrix operator * (const matrix &other) const {
        matrix result(size);

        for (int i = 0; i < size; ++i) {
            for (int j = 0; j < size; ++j) {
                for (int k = 0; k < size; ++k) {
                    result.fields[i][j] += fields[i][k] * other.fields[k][j];
                    result.fields[i][j] %= MOD;
                }
            }
        }

        return result;
    }

    // vynasobi maticu s vektorom v case O(n^2), kde n je velkost matice
    vector<long long> operator * (const vector<long long> &v) const {
        vector<long long> result(v.size(), 0);

        for (int i = 0; i < size; ++i) {
            for (int j = 0; j < size; ++j) {
                result[i] += fields[i][j] * v[j];
                result[i] %= MOD;
            }
        }

        return result;
    }

    // logaritmicke umocnovanie matice
    // algoritmus je uplne rovnaky, ako ked umocnujeme normalne cisla v logaritmickom case
    matrix exp(long long n) const {
        matrix result = matrix::diagonal(size);
        matrix mul = *this;

        while (n > 0) {
            if (n & 1) result = mul * result;
            n >>= 1;
            mul = mul * mul;
        }

        return result;
    }
};

// struktura reprezentujuca stav praveho konca branky
// pocty jednotkovych brankarov uplne napravo
struct state {
    int rows[4];    // tu su ulozene samotne pocty jednotkovych brankarov v kazdom riadku

    // vyrobi stav z indexu stavu
    // stavy potrebujeme vediet indexovat, aby sme vedeli, v ktorom riadku matice sa nachadza
    static state from_index(int index) {
        state s;
        for (int i = 3; i >= 0; --i) {
            s.rows[i] = index % 4;
            index /= 4;
        }
        return s;
    }

    // opacna operacia, ako predchadzajuca funkcia
    // vrati index daneho stavu
    int index() {
        return rows[0] * 4 * 4 * 4 + rows[1] * 4 * 4 + rows[2] * 4 + rows[3];
    }

    // rekurzivne vypocitame, do akych vsetkych stavov sa priamo vieme dostat z daneho stavu
    // ak sa do jedneho stavu vieme dostat dvoma roznymi sposobmi, tak tento stav sa
    // vo vysledku bude nachadzat dva krat
    // v parametri done_rows si pamatame, kolko hornych riadkov z praveho stlpca sme uz doplnili
    vector<state> next_states(int done_rows = 0) {
        if (done_rows == 4) return { *this };   // uz sme doplnili cely pravy okraj

        vector<state> result;

        // vyskusame umiestnit vsetkych moznych brankarov na najvyssiu nezaplnenu poziciu
        for (int square_size = 1; square_size <= 4 && square_size <= 4 - done_rows; ++square_size) {
            bool fits = true;

            // overime, ci sa da dany brankar doplnit
            for (int row = done_rows; row < done_rows + square_size; ++row) {
                if (rows[row] < square_size - 1) {
                    fits = false;
                    break;
                }
            }

            // ak ano, tak ho doplnime a rekurzivne doplnime zvysok
            if (fits) {
                state partial_next_state = *this;
                if (square_size == 1) {
                    partial_next_state.rows[done_rows] = min(3, rows[done_rows] + 1);
                } else {
                    for (int row = done_rows; row < done_rows + square_size; ++row) {
                        partial_next_state.rows[row] = 0;
                    }
                }

                for (state next_state: partial_next_state.next_states(done_rows + square_size)) {
                    result.push_back(next_state);
                }
            }
        }

        return result;
    }
};

// tato funkcia nam spocita kompletnu maticu 256x256, tak, ako je popisana
// vo vzorovom rieseni
// j-te policko v i-tom riadku urcuje pocet sposobov, ako sa da zo stavu j
// dostat priamo do stavu i
matrix full_matrix() {
    matrix m(256);

    for (int state_index_a = 0; state_index_a < 256; ++state_index_a) {
        state state_a = state::from_index(state_index_a);
        for (state state_b: state_a.next_states()) {
            int state_index_b = state_b.index();

            m.fields[state_index_b][state_index_a] += 1;
        }
    }

    return m;
}

// tato funkcia odstrani z matice vsetky nulove riadky a im
// prisluchajuce stlpce
matrix reduce_matrix(matrix m) {
    vector<int> nonzero_states;

    // najprv si najdeme indexy vsetkych nenulovych riadkov
    for (int i = 0; i < m.size; ++i) {
        bool zero_row = true;
        for (int j = 0; j < m.size; ++j) {
            if (m.fields[i][j] != 0) {
                zero_row = false;
                break;
            }
        }

        if (!zero_row) nonzero_states.push_back(i);
    }

    matrix reduced(nonzero_states.size());

    // nasledne vybudujeme maticu, ktora obsahuje len tie nenulove riadky
    for (int i = 0; i < nonzero_states.size(); ++i) {
        for (int j = 0; j < nonzero_states.size(); ++j) {
            reduced.fields[i][j] = m.fields[nonzero_states[i]][nonzero_states[j]];
        }
    }

    return reduced;
}

int main() {
    matrix m = full_matrix();

    // kompletnu maticu redukujeme az kym sa neprestane zmensovat
    while (true) {
        int orig_size = m.size;

        m = reduce_matrix(m);
        if (m.size == orig_size) break;
    }

    // pociatocny vektor poctov stavov
    // na zaciatku je len jeden stav (0, 0, 0, 0)
    vector<long long> initial_counts(m.size, 0);
    initial_counts[0] = 1;

    long long n;
    cin >> n >> MOD;

    // vypocitame konecne pocty stavov v branke 4 x n peknym umocnenim matice
    vector<long long> final_counts = m.exp(n) * initial_counts;

    // a nakoniec scitame pocty konecnych stavov do samotneho vysledku
    long long result = 0;
    for (long long count: final_counts) {
        result += count;
        result %= MOD;
    }

    cout << result << endl;
}