5. Otepľovanie v Absurdistane vzorové riešenie

Zadanie

Ako iste viete, v dôsledku globálneho otepľovania sa topia ľadovce a kvôli tomu stúpajú hladiny oceánov. V niektorých nízko položených krajinách, ako je napríklad Absurdistan, to potom spôsobuje problémy. So stúpajúcou hladinou mora totiž stúpa hladina podzemnej vody a – keďže Absurdistan má veľmi priepustné podložie – s ňou aj hladina nadzemnej vody. A tak postupne v rôznych kotlinách, údoliach a priehlbinách vznikajú nové jazerá, ktorým Absurdistanci vymýšľajú nové názvy.

Úloha

Absurdistan má tvar obdĺžnika, ktorý si pre účely tejto úlohy rozdelíme na \(r \times s\) políčok. Každé políčko má svoju nadmorskú výšku¹ – celé číslo z rozsahu \(0\) až \(H\). Hladina podzemnej vody je na začiatku \(0\). Každý rok hladina vody stúpne o \(1\) a všetky políčka, ktoré sa ocitli pod hladinou (ich nadmorská výška je ostro menšia ako výška hladiny), sa zatopia.

Každé zatopené políčko v Absurdistane je oficiálne súčasťou nejakého jazera. Pre jednoduchosť predpokladajme, že názvy Absurdistanských jazier sú nezáporné celé čísla. Každý rok sa v Absurdistane zíde Kartografická Spoločnosť Patriotov a každému zatopenému políčku \(P\) určí, ktorého jazera je súčasťou, podľa nasledujúcich pravidiel:

• Každé políčko, ktoré bolo zatopené už aj rok predtým, ostáva súčasťou jazera, ku ktorému patrilo doteraz.

• Pre každé novozatopené políčko \(P\) skúsime nájsť políčko \(R\) také, že \(R\) bolo zatopené už aj pred rokom, z \(P\) sa dá dostať do \(R\) idúc iba po zatopených políčkach (pričom z jedného políčka vieme vždy ísť iba na políčka susediace stranou, ale nie na políčka susediace rohom) a cesta po vode z \(P\) do \(R\) je najkratšia možná. Políčko \(P\) sa stane súčasťou rovnakého jazera ako \(R\). Ak je viacero možných políčok \(R\), vyberieme také, ktorého jazero má najmenšie číslo.

  Ak sa z \(P\) nedá po vode dostať na žiadne políčko, ktoré bolo zatopené už pred rokom, políčko \(P\) a všetky zatopené políčka, na ktoré sa z \(P\) dá dostať, budú prehlásené za novovzniknuté jazero.

• Novovzniknutým jazerám sa názvy priradia nasledovne: Prechádzame cez všetky políčka obdlžníka, pričom postupujeme po riadkoch zhora nadol, a v rámci riadka zľava doprava. Vždy, keď nájdeme zatopené políčko patriace k nejakému novovzniknutému jazeru, ktoré ešte nemá názov, toto jazero nazveme najmenším nepoužitým nezáporným celým číslom.

Všimnite si, že keď sa v dôsledku stúpania hladiny dve jazerá zlejú do jednej súvislej vodnej plochy, oficiálne sú to stále dve rôzne jazerá s presne vymedzenými hranicami. Pre lepšie pochopenie týchto pravidiel si môžete pozrieť vzorový príklad s vysvetlením.

Vašou úlohou bude pre každé políčko zistiť číslo jazera, ku ktorému bude toto políčko patriť po \(H+1\) rokoch, teda keď už bude celý Absurdistan zatopený.

Formát vstupu

V prvom riadku vstupu sú dve kladné celé čísla \(r, s \,(r \cdot s \leq 250\,000)\) – počet riadkov a počet stĺpcov obdĺžnika. V druhom riadku je jedno kladné celé číslo \(H \,(H \leq 250\,000)\). Nasleduje \(r\) riadkov, každý z nich obsahuje \(s\) medzerami oddelených celých čísel z rozsahu \(0\) až \(H\) – nadmorské výšky jednotlivých políčok.

Formát výstupu

Vypíšte \(r\) riadkov a v každom z nich \(s\) medzerami oddelených čísel: čísla jazier, ku ktorým budú patriť jednotlivé políčka po úplnom zatopení Absurdistanu.

Príklad

Input:

8 8
4
3 1 1 1 2 2 0 0
3 1 2 2 2 0 2 1
0 0 2 2 1 0 2 1
0 0 2 2 1 2 2 1
1 3 2 2 1 1 1 1
4 4 3 3 4 4 4 4
0 0 4 3 2 1 2 0
4 0 4 2 1 0 0 3

Output:

2 2 2 2 2 0 0 0
2 2 2 2 1 1 0 0
2 2 2 1 1 1 0 0
2 2 2 1 1 1 0 0
2 1 1 1 1 1 0 0
2 1 1 1 1 1 0 0
3 3 1 5 5 5 4 4
3 3 3 5 5 5 5 4

Absurdistan bude po jednotlivých rokoch vyzerať nasledovne (modré oblasti sú zatopené, pričom svetlomodré sú novozatopené. Čísla v nezatopených políčkach udávajú nadmorskú výšku, čísla v zatopených udávajú číslo jazera):

---

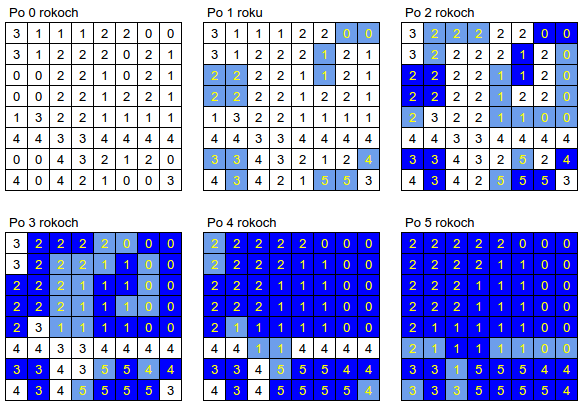
1. Pre jednoduchosť, za nadmorskú výšku budeme považovať nadmorskú výšku na začiatku zatápania, nie výšku nad aktuálnou hladinou mora. Nadmorská výška v našom chápaní sa teda počas zatápania meniť nebude.↩

Prehľadávanie do šírky

V tomto riešení budeme hojne používať štandardný algoritmus prehľadávanie do šírky (po anglicky breadth-first search, skratka BFS). O tomto algoritme existuje veľa materiálov všelikde po internete¹, preto ho v tomto vzorovom riešení nebudeme rozoberať.

Naivné riešenie

Asi najjednoduchšie riešenie, ktoré nám napadne (ak dostatočne dobre poznáme BFS) je simulovať postupne jednotlivé roky zatápania Absurdistanu a každý rok označiť novozatopené oblasti tak, ako by to urobila Kartografická Spoločnosť Patriotov (KSP). Každý rok pri tom môžeme postupovať nasledovne:

1. Spustíme BFS, ktorému povolíme prehľadávať iba zatopené políčka, naraz zo všetkých políčok, ktoré boli zatopené už minulý rok². Keď v tomto BFS z políčka \(A\) objavíme dosiaľ neobjavené novozatopené políčko \(B\), zaznačíme si, že \(B\) patrí do rovnakého jazera ako \(A\). Takýmto spôsobom bude každé novozatopené políčko priradené tomu jazeru, ktoré sa k nemu “dostalo najskôr”, teda jazeru, ku ktorému bolo dané políčko po vode najbližšie (čo je presne to, čo podľa zadania chceme).

   Ostáva ešte doriešiť, ako zabezpečiť, aby v prípade remízy vyhralo jazero s nižším číslom. To sa dá vyriešiť napríklad nasledovne:

   • BFS neimplementujeme s frontou, ale budeme ho robiť po kolách. V každom kole vezmeme všetky políčka, ktoré boli objavené v predchádzajúcom kole (špeciálne v prvom kole vezmeme všetky políčka zatopené už minulý rok) a pozrieme sa na všetkých ich novozatopených susedov. Tých z nich, ktorých sme doteraz neobjavili, si zaznačíme ako objavených v tomto kole. V prvom kole teda objavíme novozatopené políčka, ktorých vzdialenosť od najbližšieho políčka zatopeného v minulých rokoch je \(1\), v druhom kole objavíme políčka vzdialené \(2\) atď.
   • Ak v nejakom kole objavíme jedno políčko \(P\) viackrát (z rôznych smerov), pričom políčka, z ktorých sme ho objavili, patria do rôznych jazier, políčko \(P\) priradíme tomu z nich, ktoré má najmenšie číslo.

2. Následne prejdeme cez všetky políčka obdĺžnika v rovnakom poradí ako KSP (teda zhora nadol, zľava doprava). Vždy, keď nájdeme novozatopené políčko \(R\), ktoré ešte nemá určené číslo jazera, ktorému patrí (teda sme našli novovzniknuté jazero), vezmeme najmenšie číslo, ktoré sme pri označovaní jazier ešte nepoužili a týmto číslom označíme políčko \(R\). Následne spustíme z políčka \(R\) BFS idúce iba po novozatopených políčkach. Všetky políčka, ktoré toto BFS objaví, označíme rovnakým číslom jazera ako \(R\).

Odhad zložitosti

Prvá časť nášho postupu (rozširovanie už existujúcich jazier) je BFS na grafe s najviac \(r \cdot s\) vrcholmi a \(2 \cdot r \cdot s\) hranami, teda má zložitosť \(O(r \cdot s)\). V druhej časti musíme prejsť cez celú mapu, čo nás bude stáť \(O(r \cdot s)\) času a okrem toho ešte robíme nejaké BFS-ká. Keďže tieto BFS-ká púšťame v každom novovzniknutom jazere iba raz (keď objavíme prvé jeho políčko), navštívia dokopy každé novozatopené políčko neoznačené v kroku 1 práve raz, teda dokopy nám budú trvať nanajvýš \(O(r \cdot s)\) času. Odsimulovanie jedného roka nám teda bude trvať \(O(r \cdot s)\) času a potrebujeme odsimulovať \(H\) rokov, preto časová zložitosť celého algoritmu je \(O(H \cdot r \cdot s)\).

Pamäťová zložitosť je \(O(r \cdot s)\), nakoľko pre každé políčko si pamätáme iba konštantne veľa údajov a počas BFS máme v zozname vrcholov určených na prehľadanie vždy najviac \(r \cdot s\) vrcholov.

Rýchlejšie riešenie

Naše riešenie sa ešte dá podstatne zrýchliť. Stačí si uvedomiť, že veľa vecí počítame zbytočne.

Prvá zbytočná vec, ktorú robíme, je, že aj v rokoch, keď sa nič neudialo (žiadne políčko nebolo zatopené) sa snažíme označovať novozatopené políčka a strávime tým \(O(r \cdot s)\) času. Prvou optimalizáciou by teda mohlo byť na začiatku si nejako poznačiť, v ktorých rokoch sa nič neudialo a tieto roky vynechať. To môžeme urobiť napríklad nasledovne:

1. Na začiatku si vyrobíme pomocné pole dĺžky \(H+1\), kde si budeme pre každý rok pamätať, či sme videli nejaké políčko, ktoré bude zatopené v danom roku.
2. Následne postupne prejdeme všetky políčka obdĺžnika a pre každé políčko sa pozrieme, v ktorom roku bude zatopené (akú má nadmorskú výšku). K príslušnému roku si potom v našom poli poznačíme, že sa v ňom niečo udeje.

Toto celé nám bude trvať čas \(O(r \cdot s + H)\) (\(+H\) je tam preto, lebo aj vytvorenie (vynulovanie) poľa stojí nejaký čas) a urobíme to za celý algoritmus iba raz, na začiatku. Následne budeme úlohu riešiť rovnako ako predtým, teda simulovať situáciu rok po roku. Na začiatku simulovania jedného roka sa ale najprv pozrieme, či sa v danom roku niečo zmení a ak nie, daný rok preskočíme. Takto teda roky, keď sa niečo deje, odsimulujeme v čase \(O(r \cdot s)\) a roky, keď sa nič nedeje, v čase \(O(1)\). Časová zložitosť nášho algoritmu je teda \(O(r \cdot s \cdot h + H)\) (tentoraz je tam to \(+H\) preto, lebo aj v rokoch, keď sa nič neudialo, sme minuli \(O(1)\) času), kde \(h\) je počet rokov, keď sa niečo stane. Keďže rôznych nadmorských výšok môže byť na mape najviac \(r \cdot s\), platí \(h \leq r \cdot s\), preto je zložitosť nášho algoritmu v najhoršom prípade \(O(r \cdot s \cdot \min(H, r \cdot s) + H)\). Zlepšili sme sa teda v prípadoch, keď je \(H\) ďaleko väčšie ako \(r \cdot s\) a v prípadoch, keď je na mape málo rôznych nadmorských výšok.

Vidíme, že v prípadoch, keď je na mape veľa rôznych nadmorských výšok, sme si veľmi nepolepšili. V takýchto prípadoch bude totiž veľa rokov, v ktorých sa zatopí iba maličké územie, ale my kvôli nemu urobíme veľa práce. To ale tiež vieme zlepšiť. V prvom kroku simulácie jedného roka spúšťame BFS zo všetkých doteraz zatopených políčok. Mnohé z nich ale nemusia susediť so žiadnym novozatopeným políčkom a preto ich prehľadaním nič neobjavíme.

V skutočnosti by nám teda stačilo BFS spustiť iba z tých políčok, ktoré susedia s niektorým novozatopeným políčkom. Týchto políčok môže byť najviac štyrikrát viac ako novozatopených políčok, keďže každé novozatopené políčko susedí s najviac štyrmi, preto by nám BFS trvalo iba \(O(Z_i)\) času, kde \(i\) je poradové číslo daného roku a \(Z_i\) je počet políčok zatopených v tomto roku.

V druhom kroku simulácie jedného roka prechádzame celú mapu a hľadáme neoznačené novozatopené políčka, čo nám trvá \(O(r \cdot s)\) času. Ak by sme namiesto toho prechádzali iba cez novozatopené políčka a ostatné preskakovali, trvalo by nám to iba \(O(Z_i)\) času.

Nakoniec z niektorých políčok púšťame BFS. Všetky tieto BFS-ká ale dokopy prehľadajú iba všetky neoznačené novozatopené políčka, ktorých je najviac \(O(Z_i)\), teda dokopy trvajú najviac \(O(Z_i)\) času. Vylepšený algoritmus teda môže vyzerať nasledovne:

1. Úplne na začiatku si vytvoríme zoznam \(H+1\) zoznamov: pre každý rok zoznam políčok, ktoré budú v tomto roku zatopené, v poradí, v akom ich navštívi KSP (teda po riadkoch zhora nadol, v rámci riadka zľava doprava).
2. Prejdeme celú mapu, pričom každé políčko zapíšeme do zoznamu prislúchajúcemu roku, v ktorom bude dané políčko zatopené.
3. Následne simulujeme rok po roku, pričom simulácia jedného roka vyzerá nasledovne:
   1. Pozrieme sa na zoznam políčok zaplavených v tomto roku. Ak je prázdny, daný rok môžeme preskočiť. Ak nie, pre všetky políčka z tohto zoznamu sa pozrieme na všetkých ich susedov. Z tých susedov, ktorí boli zatopení už skôr, spustíme BFS, v ktorom popriraďujeme novozatopené políčka ich jazerám.
   2. Prejdeme znova zoznam políčok zatopených v danom roku a vždy keď nájdeme nejaké ešte nepriradené políčko, označíme toto políčko novým číslom jazera a spustíme z neho BFS, kde pooznačujeme aj zvyšok tohto novovzniknutého jazera.

Rok číslo \(i\) takto odsimulujeme v čase \(O(Z_i)\), teda dokopy nám všetky simulácie zaberú \(O(Z_1 + Z_2 + \dots + Z_{H+1}) = O(r \cdot c)\) času. Celý algoritmus teda pobeží v čase \(O(r \cdot c + H)\).

#include <cstdio>
#include <vector>
#include <utility>

using namespace std;

int r, s, h;
vector< vector< pair<int, int > > > zaplavime;  // zaplavime[kedy] = zoznam policok
vector< vector<int> > vyska;                    // sentinely maju vysku h+1, uz vyriesene -1
vector< vector<int> > jazero;                   // sentinely su NEZAPLAVENE
int NEZAPLAVENE;
int cislo_jazera = 0;

int dx[] = {-1, 0, 1, 0};
int dy[] = {0, -1, 0, 1};

vector<int> zaplav_susedov(vector<int> &v, int uroven){
    vector<int> susedia;
    for(int i=0; i<v.size(); i+=2){
        int y = v[i], x = v[i+1];
        for(int s=0; s<4; s++){
            int ny = y + dy[s];
            int nx = x + dx[s];
            if (vyska[ny][nx] == uroven && jazero[ny][nx] > jazero[y][x]){
                susedia.push_back(ny);
                susedia.push_back(nx);
                jazero[ny][nx] = jazero[y][x];
            }
        }
    }

    vector<int> unikatni_susedia;
    for(int i=0; i<susedia.size(); i+=2){
        int y = susedia[i], x = susedia[i+1];
        if (vyska[y][x] != -1){
            vyska[y][x] = -1;
            unikatni_susedia.push_back(y);
            unikatni_susedia.push_back(x);
        }
    }
    return unikatni_susedia;
}

void zaplav_hladinu(int hladina){
    // najdeme tych, co susedia so zaplavenymi
    vector<int> na_zaplavenie;
    for(int i=0; i<zaplavime[hladina].size(); i++){
        int y = zaplavime[hladina][i].first;
        int x = zaplavime[hladina][i].second;
        for(int s=0; s<4; s++){
            int ny = y + dy[s];
            int nx = x + dx[s];
            if (jazero[ny][nx] != NEZAPLAVENE){
                na_zaplavenie.push_back(ny);
                na_zaplavenie.push_back(nx);
            }
        }
    }

    while(na_zaplavenie.size() > 0)
        na_zaplavenie = zaplav_susedov(na_zaplavenie, hladina);

    // najdeme tych, co sme este nezaplavili
    for(int i=0; i<zaplavime[hladina].size(); i++){
        int y = zaplavime[hladina][i].first;
        int x = zaplavime[hladina][i].second;
        if (jazero[y][x] == NEZAPLAVENE){
            jazero[y][x] = cislo_jazera;
            cislo_jazera++;
            vyska[y][x] = -1;
            vector<int> na_zaplavenie;
            na_zaplavenie.push_back(y);
            na_zaplavenie.push_back(x);
            while(na_zaplavenie.size() > 0)
                na_zaplavenie = zaplav_susedov(na_zaplavenie, hladina);
        }
    }
}

int main(){
    scanf(" %d %d %d", &r, &s, &h);
    NEZAPLAVENE = (r+2)*(s+2);
    zaplavime.resize(h+1);
    vyska.resize(r+2, vector<int>(s+2, h+1));
    jazero.resize(r+2, vector<int>(s+2, NEZAPLAVENE));
    
    for(int i=1; i<r+1; i++) 
        for(int j=1; j<s+1; j++){
            int v;
            scanf(" %d", &v);
            vyska[i][j] = v;
            zaplavime[v].push_back(make_pair(i, j));
        }

    for(int hladina=0; hladina<=h; hladina++)
        zaplav_hladinu(hladina);

    for(int i=1; i<r+1; i++)
        for(int j=1; j<s+1; j++)
            printf("%d%c", jazero[i][j], (j==s) ? '\n' : ' '); 
    return 0;
}