Zadanie
Veľký vezír Kárespes sedí na svojom zlatom tróne v trónnej saune vo svojom čiernom paláci. Para mu stúpa do hlavy a s ňou vysoké myšlienky o dokonalej ekonomike. Vezír Kárespes je totiž ekonomický mysliteľ a idealista.
Čo to už aj vymyslel. V jeho krajine žije kopa obchodníkov, priekupníkov, čarodejníc a čarodejníkov (aj čarodejníčat) a všetci potrebujú kupovať a predávať (aspoň to im vezír Kárespes natĺkol do hlavy). Samozrejme, keďže vezír je ekonomický idealista, nedovolí, aby sa v jeho krajine praktizoval voľný obchod, veď to by o chvíľu skrachovalo. Ekonomika musí byť vyvážená a dokonalá.
Hlavný princíp Kárespesovej ekonomiky je tzv. “zmeň a keš” (tak to nenazval vezír Kárespes, ale kto si má zapamätať ten latinský názov). Ten spočíva v tom, že dvaja ľudia si vymenia nejaký tovar (“zmeň”) a jeden za to druhému ešte aj niečo zaplatí (“keš”). Napríklad, Saxana dá Voldemortovi gumený nos, on jej dá elastické rukavice, a keďže gumený nos má väčšiu hodnotu, tak Voldemort ešte zaplatí Saxane zopár dukátov.
Samozrejme, nie je dovolené takýmto spôsobom obchodovať úplne ľubovoľne. Veľký vezír Kárespes každému poddanému vo svojej ríši nariadil, čo môže vymieňať za čo a koľko má pri tom platiť alebo dostať.
Navyše, aby v ríši nenastal chaos, zmätok, alebo krach, vezír zariadil, aby nebolo možné tento systém oblafnúť. Predstavte si, že by som si mohol u niekoho vymeniť žabu za mačku a u niekoho iného mačku za žabu a zarobiť na tom. Potom by som mohol chodiť od jedného k druhému, vymieňať a vymieňať a zarobiť neobmedzené množstvo peňazí. Vezír však na toto myslel a preto zariadil, aby žiadne takéto triky neboli možné.
Zatiaľ čo sa vezír Kárespes zvlhčuje v saune, rybár Asymptot ulovil zlatú rybku. A tá mu sľúbila, že mu dá úplne hocičo. Samozrejme iba jeden kus. A samozrejme, že nie úplne hocičo, ale nejaký tovar. A chudák rybár Asymptot rozmýšľa, čo si má vybrať. Pomôžete mu s tým?
Úloha
Dostanete počet predmetov a potom nariadenia, ako vezír Kárespes prikázal obchodovať s danými predmetmi. Každé nariadenie hovorí, ktorý predmet je možné vymeniť za ktorý a koľko za takúto výmenu dostanete peňazí. (Napríklad, ak čarodejnica z tmavého lesa dostala nariadenie, že má vymieňať mušie krídla za hadie chvosty a dať za to 5 dukátov, tak za ňou môže niekto prísť, dať jej mušie krídla, dostane hadie chvosty a ešte aj 5 dukátov. Nemôže však urobiť opačnú výmenu – dať hadie chvosty a dostať mušie krídla – pokiaľ čarodejnica nemá aj takéto nariadenie.)
Navyše platí, že ak sa z nejakého predmetu postupnými výmenami dostanete naspäť k tomu istému predmetu, nezarobíte na tom nič (ani neprerobíte).
Vašou úlohou je zistiť, koľko najviac peňazí môže rybár Asymptot zarobiť, ak si od zlatej rybky vypýta správny predmet.
Formát vstupu
Na prvom riadku su dve celé čísla \(n, m\) oddelené medzerou – počet predmetov a počet nariadení. Predmety si očíslujeme od \(0\) po \(n-1\).
Na ďalších \(m\) riadkoch sa nachádzajú popisy jednotlivých nariadení. Nariadenie je popísané na jednom riadku tromi celými číslami: \(a_i, b_i, c_i\). Číslo \(a_i\) určuje, ktorý tovar môže Asymptot dať, \(b_i\) určuje, ktorý dostane a \(c_i\) hovorí, koľko dukátov za takúto výmenu utŕži.
Platí \(1 \leq n, m \leq 10^6\), \(0 \leq a_i,b_i < n\) a \(|c_i| \leq 10^9\).
Formát výstupu
Na jediný riadkok vypíšte jedno celé číslo – najväčší počet dukátov, ktorý vie rybár Asymptot zarobiť, ak si od zlatej rybky vypýta správny predmet.
Príklady
Input:
4 3
0 1 -1
1 2 -1
2 3 -1Output:
0Neoplatí sa obchodovať.
Input:
4 5
0 1 1
1 2 -3
2 3 4
3 0 -2
2 0 2Output:
4Než sa pustíte to čítania, odporúčam si naštudovať silno súvislé komponenty.
Preveďme teda našu úlohu do grafovej terminológie. Zadaný je ohodnotený orientovaný graf taký, že každý sled začínajúci a končiaci v tom istom vrchole má celkové ohodnotenie \(0\). (Sled je, neformálne povedané, ľubovoľná prechádzka v grafe.) Úlohou je nájsť najväčšie číslo také, že v grafe existuje sled s takým celkovým ohodnotením.
Zrejme nám stačí v grafe hľadať cestu s najväčším celkovým ohodnotením – ak sme totiž nejaký vrchol navštívili dvakrát, tú časť sledu môžeme vynechať, nakoľko má celkové ohodnotenie \(0\). (Cesta je sled, v ktorom každý vrchol navštívime najviac raz.)
Jedným z možných riešení je Floyd-Warshallov algoritmus. Ten môžeme použiť, nakoľko graf neobsahuje cykly s kladným celkovým ohodnotením. Je ale pomalé a zbytočne silné – nehľadá totižto len dĺžku najdlhšej cesty, ale hľadá dĺžky najdlhších ciest medzi každou dvojicou vrcholov.
Ďalej sa budeme snažiť zredukovať zadaný problém na hľadanie cesty z najväčším ohodnotením v acyklickom grafe. Tento problém sa totižto dá jednoducho riešiť pomocou rekurzie s memoizáciou, alebo pomocou dynamického programovania.
Všimneme si nasledovné pozorovanie: nech existuje cesta z \(A\) do \(B\), a tiež nech existuje cesta z \(B\) do \(A\) s celkovým ohodnotením \(q\). Potom každá cesta z \(A\) do \(B\) má rovnaké celkové ohodnotenie rovné \(-q\).
Z predchádzajúceho pozorovania vyplýva: nech \(A, B, C\) patria do toho istého silno súvislého komponentu. Potom namiesto toho, aby sme uvažovali cestu z \(A\) do \(C\), nám stačí uvažovať cestu z \(A\) do \(B\) a cestu z \(B\) do \(C\) – tie majú dokopy rovnaké ohodnotenie, ako pôvodne zamýšľaná cesta z \(A\) do \(C\). Naskytá sa nám tak nasledujúca úvaha: z každého silno súvislého komponentu \(\lbrace A_1, \ldots, A_n \rbrace\) vyberieme jedného reprezentanta. Nech to je \(A_1\). Pre všetký ostatné vrcholy \(A_i\) vypočítame ohodnotenie cesty z \(A_1\) do \(A_i\). Nech je to ohodnotenie rovné \(q\). Vytvoríme hranu s hodnotou \(q\) vedúcu z \(A_1\) do \(A_i\), a hranu s hodnotou \(-q\) z \(A_i\) do \(A_1\). Pôvodné hrany súvislého komponentu zmažeme.
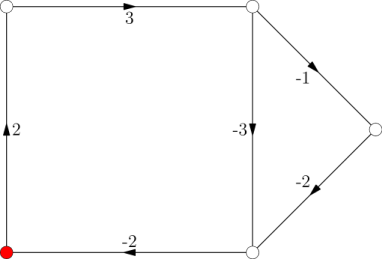
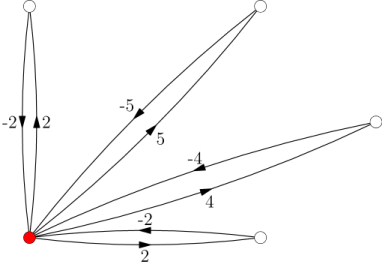
Ľahko nahliadneme, že odpoveď pre takto zostrojený graf je rovnaká, ako odpoveď pre pôvodný graf. Tento graf ale ešte nie je acyklický – na to si ešte všimneme, že nikdy nepotrebujeme navštíviť reprezentanta dvakrát. Rozdelíme teda každý vrchol \(A\) silno súvislého komponentu, ktorý nie je reprezentant, na dve – vstupný vrchol \(A_{in}\) a výstupný vrchol \(A_{out}\). Zo vstupného vrcholu vedie jediná hrana z \(A_{in}\) do reprezentanta, a vedú doňho rovnaké hrany, ako viedli do pôvodného vrcholu \(A\). Do výstupného vrcholu vedie jediná hrana z reprezentanta do \(A_{out}\), a vychádzajú z neho rovnaké hrany, ako vychádzali z pôvodného vrcholu \(A\).
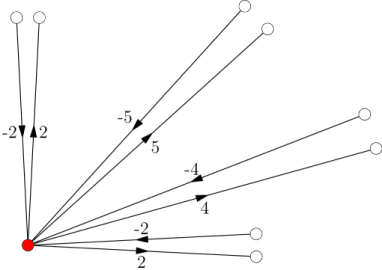
Toto spravíme pre každý silno súvislý komponent. Silno súvislé komponenty vieme nájsť napríklad pomocou Tajranovho algoritmu na hľadanie silno súvislých komponentov. Vzniknutý graf je zrejme acyklický, tak na ňom spustíme riešenie pre acyklické grafy.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.