1. Trasy lodí vzorové riešenie

3
101
10 20
15 25
70 60

1

3
101
97 3
6 94
91 10

0

4
101
0 50
25 75
20 80
82 22

4

Zadanie úlohy bolo jednoduché: máme kruh a ním prechádzajúce priamky, spočítajte dvojice priamiek, ktoré sa vo vnútri kruhu križujú. Celé je to ešte zjednodušené tým, že priesečníky priamiek s kruhom sú všetky navzájom rôzne.

Za túto úlohu je hanba mať nulu, pretože riešenie hrubou silou – presnejšie, v čase \(\Theta(n^2)\) – je veľmi jednoduché. Pre každú dvojicu priamiek vieme v konštantnom čase spočítať, či sa križujú alebo nie: Ak máme priamku spájajúcu body \(a\) a \(b\), pričom \(a<b\), a druhú priamku spájajúcu body \(c\) a \(d\), tak sa križujú vo vnútri kruhu vtedy a len vtedy, ak práve jedno z čísel \(c\) a \(d\) leží v intervale \((a,b)\). Rozmyslite si to pri pohľade na nasledujúci obrázok:

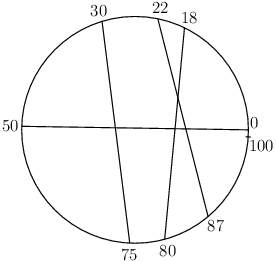
Veselšie to samozrejme bude akonáhle sa pokúsime o riešenie s lepšou časovou zložitosťou.

Základná myšlienka nášho riešenia pritom nebude vôbec zložitá. Mnohé problémy na kruhu sa dajú previesť na problémy na priamke, a tie sa väčšinou dajú riešiť jednoduchšie. Presne o to sa pokúsime aj v našom vzorovom riešení.

Predstavme si, že sme zobrali nožnice a prestrihli kruh medzi ľubovoľnými dvomi z bodov zadaných na vstupe – napríklad medzi bodmi s číslom \(0\) a \(r\). (Na našom obrázku teda medzi bodmi 0 a 100.) Kruh teraz chytíme za oba konce a vystrieme ho na úsečku. Pre kruh z príkladu vyššie by sme takto dostali nasledovnú úsečku:

Každá z pôvodných priamok (presnejšie, tetív našej kružnice) sa teraz zmenila na nejaký interval na našej úsečke. Dôležité je uvedomiť si, že tieto intervaly naďalej nesú všetku informáciu potrebnú na vyriešenie úlohy. (Totiž nijak sme nezmenili čísla zo vstupu, len sa na ne inak pozeráme.) A navyše túto informáciu z nich vieme ľahko získať:

• Dvojica tetív zodpovedajúca disjunktným intervalom sa nepretína.
• Dvojica tetív zodpovedajúca intervalom z ktorých je jeden celý vnútri druhého sa nepretína.
• Všetky ostatné dvojice tetív sa pretínajú.

Inými slovami, stačí nám zistiť počet dvojíc intervalov, ktoré sa len čiastočne prekrývajú: teda idúc zľava doprava najskôr začne prvý interval, potom začne druhý, potom skončí prvý a až po ňom skončí druhý interval.

Tento počet dvojíc vieme ľahko určiť zametaním. Začneme tým, že si všetky začiatky a konce našich intervalov uložíme do jedného poľa a toto pole usporiadame. V tomto poradí ich teraz budeme spracúvať.

A čo sa bude diať počas tohto spracúvania? Budeme si (v nejakej šikovnej podobe, ktorú upresníme neskôr) pamätať, ktoré intervaly sú momentálne otvorené – teda množinu intervalov, ktorých začiatok sme už spracovali ale koniec ešte nie. Vždy, keď spracujeme ďalší začiatok intervalu, pribudne nám nejaký interval do tejto množiny, a vždy, keď spracujeme koniec, tak nám z nej jeden interval ubudne.

Navyše vždy, keď spracúvame koniec nejakého intervalu, započítame nejaké dvojice čiastočne sa prekrývajúcich intervalov – tie, v ktorých je interval, ktorý práve skončil, “prvý”. Koľko je takých dvojíc? “Druhým” intervalom v každej takejto dvojici je určite niektorý z intervalov, ktoré sú práve otvorené. Treba si ale uvedomiť, že my nechceme úplne všetky takéto intervaly – len tie z nich, ktoré začali neskôr ako náš interval, ktorého koniec práve spracúvame.

Potrebujeme teda vedieť efektívne odpovedať na otázky nasledujúceho typu: “Koľko spomedzi intervalov ktoré sú práve otvorené, má začiatok medzi \(x\) a \(y\)?” Toto vieme spraviť veľa rôznymi spôsobmi. Napríklad môžeme použiť vyvažovaný binárny vyhľadávací strom, v ktorého vrcholoch si pamätáme začiatky aktuálne otvorených intervalov, a navyše informáciu o tom, koľko vrcholov stromu sa pod ním nachádza. Pomocou takejto dátovej štruktúry vieme ľubovoľnú otázku vyššie uvedeného typu zodpovedať v logaritmickom čase.

Existujú však aj stručnejšie možnosti implementácie. K tým nám môže pomôcť napríklad to, že si uvedomíme, že na konkrétnych súradniciach začiatkov a koncov našich intervalov vôbec nezáleží. Keď už ich raz usporiadame, riešenie sa vôbec nezmení, ak ich následne prečíslujeme na \(1\) až \(2n\). No a udržiavať si podmnožinu množiny \(\{1,\dots,2n\}\) je už výrazne ľahšie ako robiť to vo všeobecnosti. Môžeme na to použiť napríklad intervalový strom (ľudovo nazývaný intervaláč) alebo Fenwickov strom (u nás ľudovo nazývaný fínsky strom, pozri ). Ten druhý používame aj v našej nižšie uvedenej implementácii.

Všetky vyššie popísané riešenia majú zjavne časovú zložitosť \(\Theta(n\log n)\) a pamäťovú \(\Theta(n)\).

#include <algorithm>
#include <iostream>
#include <map>
#include <set>
#include <vector>
using namespace std;

struct FenwickTree {
    int fsize;
    vector<int> F;

    FenwickTree(int sz) { fsize=1; while (fsize<sz) fsize <<= 1; F.clear(); F.resize(fsize+1); }

    void update(int x, int d) { while (x <= fsize){ F[x]+=d; x+=x&-x; } }

    int sum(int x1, int x2) { // sucet v zlava-otvorenom intervale (x1,x2]
        int res = 0;
        while (x2) { res += F[x2]; x2 -= x2 & -x2; }
        while (x1) { res -= F[x1]; x1 -= x1 & -x1; }
        return res;
    }
};

struct event { 
    long long kde;
    int id, typ;
    event(long long kde, int id, int typ) : kde(kde), id(id), typ(typ) {}
};

bool operator< (const event &A, const event &B) { return A.kde < B.kde; }

int main() {
    int N; cin >> N;
    long long R; cin >> R;
    
    vector<long long> Z(N); // Z[i] je zaciatok intervalu cislo i
    vector<event> events;
    for (int n=0; n<N; ++n) {
        long long z, k; cin >> z >> k; if (z>k) swap(z,k);
        Z[n] = z;
        events.push_back( event(z,n,+1) );
        events.push_back( event(k,n,-1) );
    }
    sort( events.begin(), events.end() );

    for (int n=0; n<2*N; ++n) { // precislujeme suradnice na 1 az 2N
        events[n].kde = n+1;
        if (events[n].typ == +1) Z[ events[n].id ] = n+1;
    }

    FenwickTree F(2*N+7);
    long long answer = 0;
    for (auto e : events) {
        if (e.typ == +1) {
            F.update(e.kde,+1);
        } else {
            int my_start = Z[e.id];
            F.update(my_start,-1);
            answer += F.sum(my_start,e.kde);
        }
    }
    cout << answer << endl;
}

 Bonus na záver

Štandardný set v C++ veci potrebné na riešenie tejto úlohy robiť nevie. Konkrétne, nevie nám odpovedať na otázku, koľko spomedzi v ňom uložených prvkov leží v danom intervale. Netreba však hneď implementovať vlastný strom. V novších verziách g++ kompilátora nájdeme aj takzvané “policy-based data structures” a medzi nimi aj stromy, ktoré potrebnú fičúriu majú. A s nimi je už riešenie našej úlohy hračkou.

#include <algorithm>
#include <iostream>
#include <map>
#include <set>
#include <vector>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;

typedef tree< long long, null_type, less<long long>, rb_tree_tag, tree_order_statistics_node_update > ordered_set;

struct event { 
    long long kde, zac;
    int id, typ;
    event(long long kde, long long zac, int id, int typ) : kde(kde), zac(zac), id(id), typ(typ) {}
};

int main() {
    int N; cin >> N;
    long long R; cin >> R;
    
    vector<event> events;
    for (int n=0; n<N; ++n) {
        long long z, k; cin >> z >> k; if (z>k) swap(z,k);
        events.push_back( event(z,z,n,+1) );
        events.push_back( event(k,z,n,-1) );
    }
    sort( events.begin(), events.end(), [](const event &A, const event &B) { return A.kde < B.kde; } );

    long long answer = 0;
    ordered_set open;
    for (auto e : events) {
        if (e.typ == +1) {
            open.insert(e.zac); 
        } else { 
            open.erase(e.zac);
            answer += open.order_of_key(e.kde) - open.order_of_key(e.zac);
        }
    }
    cout << answer << endl;
}

(Tento strom podporuje aj operáciu inverznú k order_of_key: metóda find_by_order(x) vráti iterátor na \(x\)-tý najmenší prvok, číslujúc od nuly. Obe operácie bežia v čase logaritmickom od počtu uložených prvkov.)

 Bonus za záverom

Ak by niekedy došlo na najhoršie a bolo naozaj treba od základov implementovať vlastný vyvažovaný strom, dôležité je dodržať dve zásady:

• nepodľahnúť panike
• vedieť, aký strom implementovať

Hrdinom dnešných dní je treap (): strom, ktorý na to, aby bol s veľkou pravdepodobnosťou vyvážený, používa náhodné čísla. Keď porozumiete tomu, ako treap funguje, je jeho implementácia (spravená správnym spôsobom) až prekvapivo stručná a takmer bez špeciálnych prípadov. Trik na dobrú implementáciu je nasledovný:

• jediným rekurzívnym prechodom zhora dole vieme treap rozbiť na dva menšie (split)
• taktiež jediným prechodom zhora dole vieme tie dva menšie spojiť späť (merge)
• vkladanie prvku aj výber prvku vieme triviálne realizovať pomocou split a merge
• čokoľvek ďalšie dorobíme rovnako ako by sme to robili v nevyvažovanom strome

Tu je v celej jej kráse implementácia, ktorá sa dá priamo použiť v predchádzajúcom riešení namiesto ordered_tree.

struct treap {
    struct treap_node {
        long long x; // prvok ktory si pamatame
        int y;       // nahodna priorita
        int size;    // velkost podstromu pod tymto vrcholom
        treap_node *l, *r;

        treap_node(long long x) : x(x), y(rand()), size(1), l(NULL), r(NULL) {}
        ~treap_node() { delete l; delete r; }

        void refresh() { size = 1 + (l ? l->size : 0) + (r ? r->size : 0); }
    };

    void split(treap_node *root, long long x, treap_node* &l, treap_node* &r) {
        // rozdeli treap na dva: lavy obsahujuci hodnoty <x a pravy obsahujuci >=x
        l = r = NULL;
        if (!root) return;
        if (root->x < x) { split(root->r, x, root->r, r); l=root; }
        else             { split(root->l, x, l, root->l); r=root; }
        root->refresh();
    }

    treap_node* merge(treap_node *l, treap_node *r) {
        // undo split
        if (!l || !r) return l ? l : r;
        treap_node *p;
        if (l->y < r->y) { p=l; p->r = merge(p->r,r); } else { p=r; p->l = merge(l,p->l); }
        p->refresh();
        return p;
    }

    treap_node *root;

    treap() : root(NULL) {}
    ~treap() { delete root; }

    void insert(long long x) {
        treap_node *l, *r;
        split(root,x,l,r);
        root = merge(merge(l,new treap_node(x)),r);
    }

    void erase(long long x) {
        treap_node *l, *m, *r;
        split(root,x,l,r);
        split(r,x+1,m,r);
        if (m) delete m;
        root = merge(l,r);
    }

    int order_of_key(long long x) {
        treap_node *l, *r;
        split(root,x,l,r);
        int answer = l ? l->size : 0;
        root = merge(l,r);
        return answer;
    }
};