Zásobník (stack), rad (queue), obojsmerný rad (deque)

Zásobník, rad a obojsmerný rad patria medzi základné dátové štruktúry, s ktorými sa pravdepodobne stretnete, nech už budete programovať čokoľvek.

Zásobník

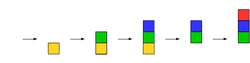
Zásobník (stack) si vieme predstaviť ako krabice naukladané na sebe tak, že tvoria vežu. Novú krabicu môžeme pridať len na vrch, a odoberať krabice môžeme tiež len z vrchu. Okrem toho máme k dispozícii ešte jednu operáciu: môžeme sa pozrieť, čo je vo vrchnej krabici. V súvislosti so zásobníkom sa môžeme stretnúť aj s názvom LIFO -- "last in, first out", čiže "posledný dnu, prvý von" (pretože krabica, ktorú vezmeme zo zásobníka ako prvú, je tá, ktorú sme na zásobník položili ako poslednú).

Na čo je zásobník dobrý? Môžeme ním implementovať napríklad operáciu "undo" (späť) v textovom editore (a mnoho iných vecí) -- keď píšeme, každá zmena, ktorú v dokumente spravíme, sa uloží na zásobník. Keď klikneme na "undo" alebo stlačíme zodpovedajúcu kombináciu kláves, textový editor vytiahne zo zásobníka poslednú operáciu, ktorú sme spravili, a vykoná ju "naopak", čím uvedie dokument do stavu pred ňou.¹

Zásobník je abstraktná dátová štruktúra, čo znamená, že keď hovoríme o zásobníku, nemáme na mysli žiadnu konkrétnu implementáciu, ale len abstraktný objekt, ktorý podporuje nasledovné (vyššie spomínené) operácie:

• pridať prvok (na vrch),
• odobrať prvok (z vrchu),
• pozrieť sa na vrchný prvok.

Tieto tri operácie môžeme implementovať viacerými spôsobmi. Jednou z možných implementácií je implementácia pomocou poľa: vytvoríme si pole $A$ dlhé $n$ a premennú $vrch$, ktorá označuje, na ktorom indexe poľa sa nachádza vrchný prvok zásobníka. Na začiatku nastavíme $vrch = -1$ (pretože zásobník je prázdny, a teda sa jeho vrchný prvok nenachádza na žiadnom indexe v poli). Keď chceme pridať prvok, skontrolujeme, či $vrch + 1 < n$, a ak to platí, tak zväčšíme $vrch$ o $1$ a vložíme nový prvok na $vrch$-té miesto poľa $A$. (Ak je $vrch + 1$ rovný $n$, tak je celé pole plné, takže sa nám doň nový prvok nezmestí -- vtedy môžeme napríklad vyhlásiť chybu, alebo si vytvoriť nové, dlhšie pole, do ktorého prekopírujeme celý obsah poľa $A$ a pole $A$ zahodíme.) Keď chceme odobrať prvok, skontrolujeme, či $vrch \geq 0$, a ak to platí, tak zmenšíme $vrch$ o 1.² (Ak je $vrch$ menší ako $0$, znamená to, že zásobník je prázdny a nemáme aký prvok odobrať.) No a napokon, ak sa chceme pozrieť na vrchný prvok zásobníka, pozrieme sa na $A[vrch]$.

Ďalšou možnosťou je implementácia pomocou obojsmerne spájaného zoznamu. V tomto prípade nám stačí si pamätať pointer na posledný prvok zoznamu (resp. nulový pointer, ak je zásobník prázdny). Pri vkladaní nového prvku vyrobíme nový prvok zoznamu, prepojíme ho s doterajším posledným a zapamätáme si pointer naň ako pointer na posledný prvok. Pri vyberaní postupujeme naopak. (Samozrejme, nezabudneme skontrolovať, či náhodou zoznam -- a teda aj zásobník -- nebol prázdny.) Ak sa chceme pozrieť na posledný prvok, jednoducho budeme nasledovať pointer, ktorý si pamätáme.

Obe implementácie majú rovnaké zložitosti. Pamäťová zložitosť celej štruktúry je $n$. Časové zložitosti jednotlivých operácií sú rovnaké -- $O(1)$. (Toto platí iba ak sa pri implementácii poľom uspokojíme v prípade plného poľa s vyhlásením chyby. Ak namiesto toho vytvoríme nové pole a pôvodné do neho budeme chcieť nakopírovať, v najhoršom prípade bude mať operácia pridania nového prvku lineárnu časovú zložitosť.)

Rad

Rad (queue alebo aj fronta) funguje presne ako rad v supermarkete pri pokladni. Nový zákazník sa vždy postaví na koniec radu, a pokladníčka vždy obslúži toho, kto je na začiatku. Okrem toho máme k dispozícii ešte jednu operáciu -- môžeme sa pozrieť na to, kto je na začiatku. V súvislosti s radom sa môžeme stretnúť aj s názvom FIFO -- "first in, first out", čiže "prvý dnu, prvý von" (pretože zákazník, ktorý sa do radu postavil ako prvý, bude aj prvý obslúžený).

Rad má, podobne ako zásobník, mnoho využití.³ Môžeme si ním pomôcť napríklad pri implementovaní správania sieťovej tlačiarne -- tá zvláda tlačiť len nejaké množstvo strán za sekundu (povedzme jednu), ale pritom jej môže prikázať tlačiť mnohostranné dokumenty hneď za sebou niekoľko používateľov. V takom prípade si tlačiareň ukladá nové dokumenty do radu a keď dotlačí to, čo mala začaté, pustí sa vždy do toho dokumentu, ktorý čakal najdlhšie (čiže do toho, ktorý prišiel prvý).

Rad je tiež abstraktná dátová štruktúra. Podporuje nasledovné operácie:

• pridať prvok (na koniec),
• odobrať prvok (zo začiatku),
• pozrieť sa na prvý prvok.

Tieto operácie vieme, podobne ako pri zásobníku, implementovať viacerými spôsobmi. Zrejme najintuitívnejší je spájaný zoznam: pamätáme si pointre $prvy$ na prvý a $posledny$ na posledný prvok zoznamu. Keď chceme pridať nový prvok do radu, pridáme ho na koniec zoznamu a aktualizujeme si $posledny$ tak, aby ukazoval na novopridaný prvok. Keď chceme odobrať prvý prvok radu, aktualizujeme $prvy$ tak, aby ukazoval na nasledovníka prvku, na ktorý $prvy$ ukazoval predtým. Keď sa chceme pozrieť na prvý prvok, pozrieme sa na miesto, kam ukazuje $prvy$.

S implementáciou pomocou poľa je to trochu zložitejšie. So zásobníkom to bolo jednoduché preto, lebo jeho "začiatok" -- miesto, kde je uložený najstarší prvok -- sa nehýbal. Rad sa ale hýbe -- predlžuje sa do jedného smeru a skracuje sa z druhého. Čo sa s tým dá robiť? Mohli by sme zakaždým, keď vyberieme prvý prvok z radu, celý rad posunúť. Toto by ale dlho trvalo (pre rad s $n$ prvkami by bolo treba $n$, čiže lineárne veľa, operácií). Naštastie, tento problém vieme vyriešiť malým trikom: namiesto toho, aby sme posúvali rad, posunieme "pokladňu" -- čiže smerník na prvý prvok. (Toto funguje tak, ako keby sme mali pole "zahnuté" do kruhu -- za posledným políčkom nasledujú prvé políčko.) Implementácia teda vyzerá takto: pamätáme si pole $A$ dĺžky $n$, index $zaciatok$ a premennú $k$, v ktorej máme uložené, koľko prvkov je v aktuálne v rade. Keď chceme pridať nový prvok, a platí $k < n$, prvok vložíme na miesto $A[(zaciatok + k) \% n]$⁴ a $k$ zväčšíme o $1$. (Ak $k = n$, tak je pole plné, a nový prvok sa doň už nezmestí.) Keď chceme odobrať prvok, a platí $k > 0$, jednoducho zmeníme $zaciatok$ na $(zaciatok + 1) \% n$ a $k$ zmenšíme o $1$. (Ak $k = 0$, nemáme aký prvok odobrať, lebo rad je prázdny.) Ak sa chceme pozrieť na prvý prvok v rade, pozrieme sa na prvok $A[zaciatok]$.

Obe implementácie majú rovnaké zložitosti. Pamäťová zložitosť celej štruktúry je $n$. Časové zložitosti jednotlivých operácií sú rovnaké -- $O(1)$. (Pre rad platí rovnaká poznámka o časovej zložitosti pridávania prvku ako pre zásobník -- ak budeme mať plné pole, a budeme chcieť jeho obsah prekopírovať do nového, väčšieho poľa, bude to v najhoršom prípade trvať dlho.)

Obojsmerný rad

Obojsmerný rad⁵ (double-ended queue, čiže deque) je kombináciou zásobníka a radu. Môžeme doň vkladať aj odoberať z oboch strán, a tiež sa pozerať na začiatok aj koniec. Ako abstraktná dátová štruktúra podporuje nasledovné operácie:

• pridať prvok na koniec alebo na začiatok,
• odobrať prvok z konca alebo zo začiatku,
• pozrieť sa na prvý alebo posledný prvok.

Implementácia pomocou obojsmerne spájaného zoznamu je podobná ako pri zásobníku -- až na to, že si pamätáme dva smerníky, jeden na začiatok a druhý na koniec. Keďže používame obojsmerne spájaný zoznam, pridávanie a odoberanie prvkov na začiatku je symetrické k pridávaniu a odoberaniu prvkov na konci -- a funguje presne tak, ako fungovalo pridávanie a odoberanie prvkov v zásobníku (treba si len dať pozor na to, aby sme aktualizovali správny smerník). S pozeraním sa prvky je to tiež jednoduché -- stačí použiť správny smerník.

Implementácia pomocou poľa je podobnejšia implementácii radu. Máme také isté pole $A$ dĺžky $n$, index $zaciatok$ a premennú $k$. Keď chceme vkladať na začiatok obojsmerného radu (a používané pole nie je plné), $zaciatok$ zmeníme na $(zaciatok - 1) \% n$⁶, nový prvok vložíme na $A[zaciatok]$ a $k$ zväčšíme o $1$. Keď chceme odobrať posledný prvok (a používané pole nie je prázdne), $k$ jednoducho zmenšíme o $1$.

Obe implementácie majú rovnaké zložitosti. Pamäťová zložitosť celej štruktúry je $n$. Časové zložitosti jednotlivých operácií sú rovnaké -- $O(1)$. (Pre obojsmerný rad platí rovnaká poznámka o časovej zložitosti pridávania prvku ako pre zásobník a obyčajný rad.)