Základná grafová terminológia

Grafy, o ktorých je tento článok, sú matematické objekty skúmané v teórii grafov. Tieto grafy nemajú (okrem názvu) nič spoločné s grafmi funkcii.

Čo je to graf?

Každý graf sa skladá z dvoch zložiek (z formálneho hľadiska sú to dve množiny):

• Množina vrcholov. Vrcholy môžu byť v princípe ľubovoľné objekty a z matematického hľadiska nás veľmi nezaujíma, čo presne reprezentujú. Na obrázkoch ich zvykneme kresliť ako bodky, alebo krúžky. Množina vrcholov musí byť neprázdna a konečná (teda každý graf obsahuje jeden alebo viac vrcholov, ale musí ich obsahovať konečný počet. Množinu vrcholov zvykneme značiť $V$ (z anglického vertex) a ich počet zvykneme značiť $N$.

• Množina hrán. Hrany spájajú dvojice vrcholov (z formálneho hľadiska hrany sú dvojice vrcholov). Na obrázkoch ich zvykneme kresliť ako čiary spájajúce vrcholy. Množinu hrán zvykneme značiť $E$ (z anglického edge ) a môže byť aj prázdna. Počet hrán zvykneme značiť $M$.

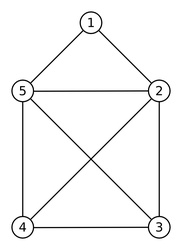
Príklad grafu môžete vidieť na obrázku. Jeho vrcholy sú 1, 2, 3, 4 a 5, hrany sú 1-2, 1-5, 2-3, 2-4, 2-5, 3-4, 3-5 a 4-5.

Na čo je to dobré?

Obrovský význam teórie grafov spočíva v tom, že veľmi veľa problémov ,,zo života'' vieme popísať vhodne zvoleným grafom. Uveďme si niekoľko príkladov:

Medziľudské vzťahy. Vrcholy budú predstavovať ľudí, hranou budú spojené tie dvojice, ktoré sa poznajú.

Počítačová sieť. Vrcholy budú predstavovať počítače, huby, switche, inteligentné chladničky... no a hrany budú káble medzi nimi.

Cestná sieť. Vrcholy budú predstavovať mestá v krajine, hrany budú cesty medzi nimi.

Šach. Každý vrchol bude predstavovať jedno rozmiestnenie figúrok na šachovnici, hranou budú spojené tie vrcholy, medzi ktorých pozíciami sa dá prejsť jedným ťahom. (Tento graf je véééľmi veľký. Zatiaľ sa zďaleka nezmestí do pamäte počítača... a aj preto ešte počítače nevedia dokonale hrať šach.)

Kreslenie jedným ťahom. Máme na papieri obrázok, ktorý chceme nakresliť jedným ťahom. Aj na ten sa vieme pozerať ako na graf: vrcholy budú priesečníky čiar, hrany budú samotné čiary.

Z informatického hľadiska to má napríklad nasledovný dôsledok: ak vymyslíme efektívny algoritmus pracujúci na grafoch, tento algoritmus potom môžeme použiť v rôznych situáciách, ktoré sa dajú reprezentovať grafmi a nemusíme vymýšľať riešenie pre každú situáciu zvlášť. Rovnaký algoritmus sa dá napríklad použiť na:

• Vyriešenie hry pätnástka na čo najmenej ťahov
• Nájdenie najkratšej cesty z Bratislavy do Košíc
• Vypočítanie, cez koľko najmenej známostí sa vie klebeta odo mňa dostať k Juhoafrickému prezidentovi

Druhy grafov

V niektorých situáciách chceme hranami v grafe reprezentovať nejaký vzťah medzi vrcholmi, ktorý nie je symetrický. Jednou z týchto situácií je napríklad aj vyššie spomínaný šach: to, že sa z jednej pozície dá jedným ťahom dostať do druhej ešte neznamená, že sa dá aj jedným ťahom dostať naspäť. V takom prípade môžeme použiť orientovaný graf. Hrany orientovaného grafu stále spájajú dvojice vrcholov, majú ale určené, v ktorom vrchole hrana začína a v ktorom končí. Z formálneho hľadiska sú to usporiadané dvojice vrcholov. Hrany orientovaného grafu zvykneme kresliť ako šípky zo začiatočného do koncového vrcholu.

Grafy, ktoré nie sú orientované voláme aj neorientované. Ak niekde hovoríme o grafe a nepovieme, či je orientovaný alebo nie, väčšinou tým myslíme neorientovaný graf.

V iných situáciách si chceme pri každej hrane pamätať ešte nejaké číslo, napríklad jej dĺžku. Príkladom takejto situácie je cestná sieť: nezaujíma nás iba to, medzi ktorými mestami vedú cesty ale aj to, aké sú tieto cesty dlhé. Keď každej hrane priradíme nejaké číslo (tomuto číslu sa zvykne hovoriť dĺžka, prípadne váha hrany), dostaneme ohodnotený graf.

Definícia grafu nevylučuje, že niektoré hrany môžu spájať vrchol s ním samým -- takéto hrany nazývame slučky. Tiež je možné, aby medzi niektorou dvojicou vrcholov viedla viac než jedna hrana -- vtedy hovoríme o násobných hranách. Graf, ktorý obsahuje násobné hrany alebo slučky voláme aj multigraf. Príkladom využitia multigrafov je vyššie spomenuté kreslenie jedným ťahom -- pre vhodné obrázky môže byť jedna dvojica vrcholov spojená viac ako jednou hranou, prípadne môže byť nejaký vrchol spojený sám so sebou.

Grafom, ktoré neobsahujú slučky ani násobné hrany hovoríme aj jednoduché grafy. Keď hovoríme o grafoch a nešpecifikujeme, či sú jednoduché alebo nie, väčšinou myslíme jednoduché grafy.

Susednosť a stupne

Hovoríme, že hrana $e$ spájajúca vrcholy $u$ a $v$ susedí (inciduje) s týmito dvoma vrcholmi. Stupeň vrcholu je počet hrán, ktoré s ním susedia.

O dvoch vrcholoch hovoríme, že spolu susedia, ak sú spojené nejakou hranou. Ak hovoríme o susedoch nejakého vrcholu, myslíme tým vrcholy (nie hrany), ktoré s ním susedia. V jednoduchých grafoch je teda stupeň vrcholu rovný počtu jeho susedov.

V orientovaných grafoch má zmysel definovať výstupný stupeň vrchola ako počet hrán, ktoré v ňom začínajú (vedú z neho von) a vstupný stupeň vrchola ako počet hrán, ktoré v ňom končia.

Sledy, ťahy, cesty

Postupnosť nadväzujúcich vrcholov a hrán (začínajúcu aj končiacu vrcholom) nazývame sled. Formálne je to konečná postupnosť

$$v_0, e_1, v_1, e_2, v_2, \dots, e_k, v_k \text{,}$$

kde $v_0, v_1, \dots, v_k$ sú vrcholy a $e_1, e_2, \dots, e_k$ sú hrany, pričom platí, že hrana $e_1$ spája vrcholy $v_0$ a $v_1$, hrana $e_2$ spája vrcholy $v_1$ a $v_2$ atď.. Neformálne sa dá na sled pozerať ako na nejakú prechádzku po grafe, kde začíname aj končíme v nejakom vrchole a medzi vrcholmi sa pohybujeme po hranách (v angličtine sa sled aj nazýva walk ). Ak hovoríme o sledoch v orientovaných grafoch, vyžadujeme, aby všetky hrany boli orientované v smere našej prechádzky (teda $e_1$ je hrana z $v_0$ do $v_1$, $e_2$ je hrana z $v_1$ do $v_2$ atď.). Dĺžku sledu definujeme ako počet hrán v ňom (ak sa nejaká hrana opakuje, rátame každý jej výskyt), prípadne pri ohodnotených grafoch ako súčet dĺžok hrán.

Sled, v ktorom sa neopakujú hrany, nazývame ťah. V príklade s kreslením jedným ťahom sa vlastne snažíme v grafe nájsť ťah, ktorý prechádza všetkými hranami.

Sled, v ktorom sa neopakujú vrcholy, nazývame cesta. Každá cesta je súčasne aj ťah -- ak by sme po nejakej hrane prešli dvakrát, museli by sme aj niektorý vrchol navštíviť dvakrát.

Ťah, ktorý sa začína aj končí v tom istom vrchole, ale okrem toho sa v ňom žiadne dva vrcholy neopakujú, nazývame cyklus, alebo kružnica. Graf, ktorý neobsahuje kružnice, voláme acyklický.

Vzdialenosť dvoch vrcholov je dĺžka najkratšej cesty medzi nimi.

Súvislosť a komponenty

Ak sa v grafe dá po hranách dostať odvšadiaľ všade, t.j. ak sú každé dva vrcholy spojené cestou, hovoríme, že graf je súvislý. Vo všeobecnosti môže graf pozostávať z niekoľkých súvislých častí, ktoré voláme komponenty súvislosti. Podobne v orientovaných grafoch, ak sa dá dostať odvšadiaľ všade v smere šípok , graf je silno súvislý.

Reprezentácia v pamäti

Na uchovávanie grafov v pamäti počítača sa väčšinou používa niektorý z nasledujúcich prístupov:

• Matica susednosti: Matica susednosti je dvojrozmerné pole, v ktorom je na pozícii [x][y] hodnota 1, ak v grafe máme hranu $x-y$, resp. hodnota 0, ak takú hranu nemáme. Pre orientovaný graf: na pozícii [x][y] je 1, ak v grafe máme hranu vedúcu z $x$ do $y$, 0 inak. Pri ohodnotených grafoch môžeme použiť maticu vzdialeností, v ktorej je buď zapísané, že hrana neexistuje (napr. je tam opäť 0), alebo je tam rovno zapísaná jej dĺžka.

  Výhodou matice susednosti je jej jednoduchosť a prehľadnosť. Avšak pokiaľ máme riedky graf (graf s málo hranami), bude nám matica susednosti zaberať zbytočne veľa pamäte. Ďalšou nevýhodou je, že aj ak má vrchol len troch susedov, musíme prejsť celý riadok matice, aby sme ich našli. Navyše v matici susednosti si nevieme zapamätať multigraf.

• Zoznam susedov: Pre každý vrchol si budeme pamätať zoznam vrcholov, do ktorých z neho vedie hrana. Najjednoduchší spôsob implementácie je opäť v dvojrozmernom poli, pričom susedov vrcholu $i$ si pamätáme v poli napr. na pozíciach [i][0] až [i][deg(i)-1] (kde deg(i) je stupeň vrcholu $i$). Keďže rôzne riadky poľa potrebujú mať rôznu dĺžku, je dobré použiť polia s premenlivou veľkosťou, teda napríklad vector<vector<int> > v C++, alebo ArrayList<ArrayList<Integer> > v Jave.

  Pre orientovaný graf si v každom vrchole si pamätáme len hrany, ktoré z neho vychádzajú. Pre ohodnotený graf si pre každú hranu musíme pamätať dve čísla: koncový vrchol a dĺžku.

• Objektovo orientovný prístup: V objektovo orientovaných jazykoch (ako napríklad Java) si môžeme pre každý vrchol pamätať jeden objekt, ktorý má referencie (smerníky) na svojich susedov. Potom nám stačí pamätať si iba zoznam všetkých vrcholov. V princípe nedostaneme nič iné ako zoznam susedov, môže to ale viesť k čitateľnejšiemu kódu, ak chceme s grafom robiť zložité operácie a napríklad si v každom vrchole pamätať nejakú pomocnú informáciu.

Špeciálne druhy grafov

Jednoduchý graf, ktorý obsahuje všetky možné hrany (teda má hranu medzi každou dvojicou vrcholov) voláme kompletný graf. Kompletný graf o $N$ vrcholoch sa zvykne označovať $K_N$.

Hovoríme, že graf je bipartitný, ak sa jeho vrcholy dajú rozdeliť na dve časti tak, že medzi žiadnymi dvoma vrcholmi z rovnakej časti nevedie hrana. Týmto dvom častiam hovoríme partície grafu. Príkladom použitia bipartitného grafu je napríklad tanečný večierok: graf, v ktorom vrcholy reprezentujú ľudí a hrany spájajú dvojice, ktoré spolu chcú tancovať, bude pravdepodobne bipartitný -- jednu partíciu budú tvoriť chlapci a druhú dievčatá.

Bipartitný graf sa niekedy definuje aj ako graf, ktorý neobsahuje cykly nepárnej dĺžky. Dá sa ukázať, že táto definícia je ekvivalentná s tou predošlou. Je zaujímavé, že napriek tomu v Slovenčine existuje slovné spojenie ,,ľúbostný trojuholník''.

Súvislý graf, ktorý neobsahuje cykly voláme strom. Dá sa ukázať, že v strome medzi každou dvojicou vrcholov existuje práve jedna cesta. Tiež sa dá ukázať, že graf s $N$ vrcholmi je strom vtedy a len vtedy, keď je súvislý a má $N − 1$ hrán.

Zakorenené stromy

V strome si často zvolíme jeden vrchol $r$ a ten nazveme koreň. Všetky hrany orientujeme smerom ku koreňu. Ak $v \neq r$ je vrchol, tak (jediný) jeho sused bližšie ku koreňu je jeho otec, susedia ďalej od koreňa sú jeho synovia (rodovo korektne ich tiež voláme rodič a deti $v$). Vrcholy, ktoré nemajú žiadnych synov voláme listy stromu. Takýto strom voláme zakorenený. Zakorenené stromy kreslíme väčšinou nasledovne: úplne na vrchu je koreň, pod ním sú jeho synovia, pod nimi sú ich synovia atď..

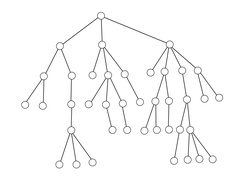
Potomkami vrcholu $v$ voláme všetky vrcholy, ktoré sú synovia $v$, synovia synov $v$ atď.. Pokiaľ uvažujeme len časť stromu obsahujúcu vrchol $v$ a jeho potomkov, tak hovoríme o podstrome stromu s koreňom $v$.

Hĺbka vrchola $v$ v zakorenenom strome je jeho vzdialenosť od koreňa.

Ak má každý vrchol, ktorý nie je list, presne dvoch synov, hovoríme o binárnom strome. Keď binárny strom nakreslíme, každý vrchol (okrem listov) bude mať dvoch synov, z ktorých jeden bude viac naľavo a druhý viac napravo. Podľa toho ich niekedy voláme ľavý syn a pravý syn.

Hoci zakorenené binárne stromy vyzerajú ako veľmi špecifický druh grafov, sú veľmi užitočné: veľa dátových štruktúr má tvar binárneho stromu. Ako príklad spomeňme napríklad haldu, väčšinu vyvažovaných vyhľadávacích stromov a intervalové stromy.