Dynamické programovanie

Dynamické programovanie je jednou z veľmi silných programátorských techník, ktorá sa dá použiť na vyriešenie veľkého počtu rozličných úloh. Bohužiaľ, názov veľmi dobre nevystihuje podstatu tejto techniky a tak si najskôr dynamické programovanie ukážeme na príkladoch a postupne sa k nemu dopracujeme.

Príklad : Nájdenie n-tého fibbonaciho čísla

Predstavme si, že máme úlohu, v ktorej máme nájsť n-tý člen Fibonacciho postupnosti. Ako si ukážeme, takýto problém má viacero možných riešení. Jedným z nich je napísať pomerne jednoduchú rekurzívnu funkciu.

int fib(int n)
{
    if(n == 1 || n == 2) return 1;
    else return fib(n-1) + fib(n-2);
}

Ak si spustíme túto funkciu, zistíme, že funkcia naozaj korektne počíta $n$-té Fibonacciho číslo avšak rýchlo zistíme, že má veľké limity v oblasti rýchlosti. Vypočítať už $50$-te číslo je pre náš program problém. Čo naša funkcia tak dlho robí?

Ak si graficky znázorníme rekurzívne volania tejto funkcie, prídeme na to, že $fib(k)$ pre $k$ od $1$ po $n$ je volaná oveľa viac ako jeden krát. (viete zdôvodniť počty jednotlivých volaní?)

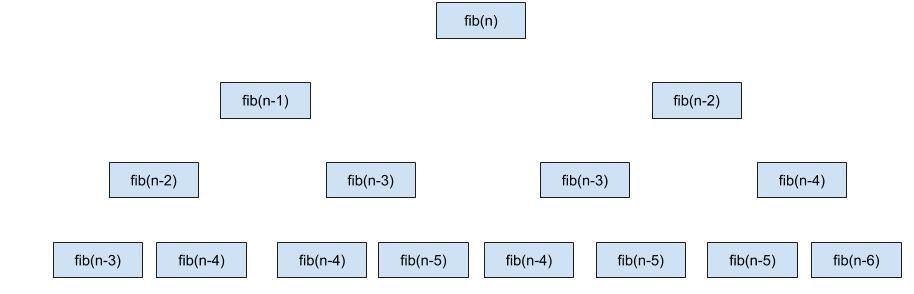
Zjavný problém teda je, že Fibonacciho funkciu rekurzívne pre to isté $k$ voláme zbytočne veľa krát. Počítať to isté dva krát určite nie je ideálne. Čo sa s tým dá robiť ?

Memoizácia

Použijeme techniku často používanú pri nepríjemných rekurzívnych funkciách a to memoizáciu. Ak naša funkcia vypočítala $fib(k)$ pre nejaké $k$, nie je nutné aby sme počítali túto funkciu odznova neskôr. Všetko, čo nám treba, je si niekde poznačiť, že sme už túto vec vypočítali a teda aj výsledok výpočtu. Ako to bude vyzerať v praxi ?

vector<int> tab(n+1, -1);
int fib(int n)
{
    if(tab[n] != -1) return tab[n];

    if(n == 1 || n == 2) tab[n] = 1;
    else tab[n] = fib(n-1) + fib(n-2);

    return tab[n];
}

Pomocou memoizácie sa nám podarilo zabezpečiť, že pri volaní $fib(n)$ bude každá funkcia tvaru $fib(k)$ kde $k \leq n$ zavolaná iba raz. S takouto funkciou už vieme vypočítať aj Fibonacciho čísla pre veľke $n$, napríklad milión. Samozrejme, problém nám už bude robiť buď pretečenie premennej v C++ alebo čas, ktorý zaberú aritmetické operácie v Pythone, keďže Fibonacciho čísla rastú exponenciálne rýchlo. Samotná funkcia však už nemá nijaké myšlienkové chyby.

Ak si chceme teda nejak zhrnúť základnú myšlienku memoizácie, je to metóda optimalizácie algoritmov pomocou zapamätania si hodnôť, ktoré by sme inak počítali viac krát.

Aby sa nám memoizácia ešte o čosi viac dostala pod kožu, vyskúšajme si nasledujúci príklad použitia tejto metódy:

Máme zadanú mriežku veľkosti $n \cdot m$. Jej riadky číslujeme $0$, $1$, $2$ až $n-1$. Stĺpce číslujeme $0$, $1$ až $m-1$. Chceme vedieť, koľkými spôsobmi vieme prejsť z ľavého horného rohu([0;0]), do pravého dolného([n-1;m-1]), pričom sa smieme pohybovať len smerom nadol alebo doprava. Teda z pozície [i;j] sa vieme dostať do pozícií [i+1][j] a [i][j+1]. Dva spôsoby prejdenia mriežky(cesty) považujeme za rôzne ak pri prechádzaní prvým spôsobom vstúpime aspoň na jedno políčko mriežky, ktoré sa nevyskytuje v druhej ceste.

Predstavme si, že sa nachádzame na políčku [n-1;m-1], na toto políčko sme sa dostali určite z jedného z políčok [n-2;m-1] alebo [n-1;m-2]. To teda znamená, že všetky možnosti ako sa dostať na políčko [n-1;m-1] vzniknú tak, že vedieme buď cestu do [n-2;m-1] alebo [n-1][m-2] a predĺžime ju o $1$. Teda počet všetkých možností bude súčtom možností ako sa dostať na políčka [n-2][m-1] a [n-1][m-2]. Tu už sa nám črtá jednoduché rekurzívne riešenie:

int f(int i, int j)
{
    if(i == 0 || j == 0) return 1;
    return f(i-1, j)+f(i, j-1);
}

int main()
{
    int n, m;
    cin >> n >> m;

    cout << f(n-1, m-1) << endl;
    return 0;
}

V rekurzívnej funkcii si ako parametre odovzdávame, kde sa práve nachádzame a funkcia vracia počet rôznych ciest, ktoré vedú do políčka daného parametrami funkcie.

Pokiaľ ste pozorne čítali, mohli ste si všimnúť, že máme tú istú situáciu, čo pri funkcii $fib()$. Rekurzívna funkcia, ktorá je pomalá a počíta niektoré veci viackrát. Tak isto ako aj predtým, vieme dostať rýchle riešenie použitím memoizácie. Tentokrát si ale musíme pamätať informácie o výsledku v dvojrozmernom poli, kedže počet parametrov funkcie je $2$.

Dynamické programovanie

Otázka je, načo sme si toto ukazovali? Čo to má s dynamickým programovaním? Uvidíme, že dynamické programovanie je v podstate memoizácia z opačnej strany. Poďme teraz vyriešiť hľadanie $n$-tého Fibonacciho čísla dynamickým programovaním. Kód by vyzeral nejak takto:

int fib(int n)
{
    vector<int> tab(n, -1);
    tab[0] = 1;
    tab[1] = 1;

    for(int i=2;i<n;++i)
    {
        tab[i] = tab[i-1] + tab[i-2];
    }

    return tab[n-1];
}

Myšlienka za týmto riešením je asi takáto. Predstavme si, že vieme $k$-te Fib. číslo a aj všetky predním, teda $k-1$, $k-2$… Ako vypočítame $k+1$ Fib. číslo ? Vieme, že nás to v podstate stojí iba jedno sčítanie, pretože všetko, čo potrebujeme, máme už vypočítané. Sčítame $k-1$ a $k-2$ Fib. číslo a dôjdeme k výsledku. Ako teraz vypočítať $k+2$ Fib. číslo ? No zjavne môžme použiť predchádzajúcu úvahu a sčítaním toho, čo už vieme, teda $k$ a $k+1$ Fibb. čísla sa dopracujeme k výsledku. Takto vieme pokračovať tak dlho, pokým nenarazíme na naše $n$-té Fib. číslo. Odkiaľ sa ale vezmú tie Fibonacciho čísla, ktoré už vieme? Vidíme, že na začiatku vieme triviálne 1. a 2. Fib. číslo. Vďaka ním vieme vypočítať aj 3. potom 4. atď. presne ako v našej úvahe. Podstata využitia dynamického programovania v tejto úlohe teda je, že na nájdenie $k$-teho Fib. čísla, nám stačí poznať riešenie o čosi "jednoduchšieho" problému a to hodnoty $k-1$ a $k-2$ Fib. čísla.

Príklad : Hľadanie najväčšieho objemu fliaš

Predstavme si, že máme v rade za sebou položených $n$ fliaš. Pre každú vieme jej kladný celý objem $v_i$. Chceme vybrať z radu niekoľko fliaš s najväčším možným objemom tak, že nevyberieme žiadne dve po sebe idúce fľaše.

Znova upriamime pozornosť na nájdenie nejakého jednoduchšieho, teda o čosi menšieho problému, ktorý nám pomôže nájsť riešenie pôvodného väčšieho problému. Predstavme si, že hľadáme riešenie len pre prvých $k$ fliaš a optimálne riešenie pre prvých $k-1$, $k-2$ ... $1$ fliaš už máme k dispozícií. Sú dve možnosti ako môže vyzerať optimálne riešenie pre prvých $k$-fliaš. Prvou možnosťou je, že do optimálneho riešenia $k$-ta fľaša patrí, druhou možnosťou je, že tam nepatrí. Prvé dôležité pozorovanie je, že riešenia pre 1. fľašu, 2., 3. atď tvoria neklesajúcu postupnosť. Totiž ak by pre nejaké $i$ a $j$ také, že $i<j$ platilo, že z prvých $i$ fliaš vieme vytvoriť objem väčší ako z prvých $j$, je to zjavný nezmysel. Totiž, vieme vytvoriť riešenie pre prvých $j$ fliaš také, že vezmeme všetky fľaše z riešenia pre prvých $i$ fliaš(to môžme kedže $i<j$) a už žiadne iné fľaše, čím dostaneme riešenie pre prvých $j$ fliaš aspoň rovné najlešiemu riešeniu pre prvých $i$ fliaš.

Vráťme sa teraz naspäť v našej úvahe ku $k$-tej fľaši. Ak do optimálneho riešenia nepatrí, je optimálne riešenie pre prvých $k$ fliaš rovné riešeniu pre prvých $k-1$ fliaš. Ak do optimálneho riešenia patrí, nemôžme už použiť riešenie pre prvých $k-1$ fliaš ale musíme použiť riešenie pre prvých $k-2$ fliaš, kedže $k-1$. fľaša určite nemôže byť použitá v tom istom riešení, kde je použitá $k$-ta fľaša.

Našli sme teda spôsob ako pomerne jednoducho z riešení pre prvých $1$, $2$... $k-1$ fliaš vypočítať riešenie pre $k$-tu fľašu. Zatiaľ sme ale predpokladali, že predchádzajúce menšie problémy máme zodpovedané. Kde na začiatku nájsť tie menšie problémy od ktorých sa "dá odraziť"? Na optimálne riešenie pre prvú a pre prvé dve fľaše isto prídete aj sami, tie tvoria vlastne základnú pôdu pre štarť nášho riešenia. Kód implementujúci toto riešenie by mohol vyzerať nejak takto:

int solve(int n, const vector<int> &objemy)
{
    vector<int> tab(n, 0);
    tab[0] = objemy[0];
    tab[1] = max(objemy[0], objemy[1]);

    for(int i=2;i<n;++i)
    {
        tab[i] = max(tab[i-1], tab[i-2] + objemy[i]);
    }

    return tab[n-1];
}

Príklad : Platenie mincami

Nachádzame sa v obchode, kde potrebujeme zaplatiť určitú kladnú celočíselnú sumu $s$. Máme k dispozícií $n$ mincí v rôznych kladných celočíselných hodnotách, pričom niektoré hodnoty sa môžu opakovať. Otázka je s koľko najmenej mincami vieme zaplatiť danú sumu $s$.

V tomto prípade je už o čosi zložitejšie dôjsť na ideálne menšie problémy, spojením ktorých by sme vedeli vyriešiť nejaký väčší, o čosi ťažší problém. Niečo nám napovie pomerne jednoduché rekurzívne riešenie. Predstavme si, že máme $n$ mincí a sumu $s$. To čo chceme docieliť je, zaplatiť ju. Ak sa pozrieme na poslednú mincu, máme dve možnosti, nepoužiť ju a mať stále zaplatiť sumu $s$ pomocou už len $n-1$ mincí alebo ju použiť a mať už zaplatiť len $s - hodnotamince_(n)$. Tu sa nám črtá rekurzia, ktorú môžme ľahko naprogramovať. Otázne ešte je, čo bude fungovať ako dno rekurzie. Tým bude, keď už budeme mať len $0$ mincí. Ak vtedy bude suma, ktorú máme ešte zaplatiť rovná $0$, našli sme jedno z riešení, to či optimálne zistíme, keď všetky takéto riešenia porovnáme a vyberieme z nich to, čo použilo najmenej mincí. Implementácia tejto rekurzívnej funkcie:

int best = 1000000;
vector<int> mince;

void funkcia(int nevyskus, int zaplatit, int pouz)
{
    if(nevyskus == 0)
    {
        if(zaplatit == 0) best = min(best, pouz);
        return;
    }

    funkcia(nevyskus-1, zaplatit, pouz);
    funkcia(nevyskus-1, zaplatit-mince[nevyskus-1], pouz+1);
}

int main()
{
    int n, s;
    cin >> n >> s;

    mince.resize(n);
    for(int i=0;i<n;++i) cin >> mince[i];

    funkcia(n, s, 0);
    cout << best << endl;

    return 0;
}

Ako parametre tu používame, počet mincí, ktoré sme ešte nezvážili do riešenia, sumu, ktorú nám ešte ostáva zaplatiť a počet mincí, ktoré sme pri doterajšom platení použili. Samozrejme, táto rekurzia nebude nijak extra rýchla. Aj keď ju je možné zrýchliť memoizáciou, nemusí to byť úplne to pravé orechové, kedže si stavy musíme už pamätať v trojrozmernom poli/liste/vektore, ktorý je značne rozmerný.

Ak sa ešte trochu zamyslíme, môžme využiť niektoré pozorovania z predchádzajúceho riešenia. V rekurzii sme vlastne pomali prichádzali o mince a nejak nám to menilo hodnotu, ktorú ešte máme zaplatiť. Ak si vezmeme klasický prístup dynamiky "odspodu". Čo keby sme na začiatku nemali mince a nevedeli nič zaplatiť a postupným pridávaním mincí by sa nám zväčšoval počet súm, ktoré vieme zaplatiť a aj zmenšoval počet mincí, pomocou ktorých dané sumy zaplatíme?

Práve toto je kľúč k dynamickému riešeniu tejto úlohy. Budeme riešiť problémy : Na koľko najmenej mincí idú zaplatiť sumy od $0$ po $s$ pomocou prvých $0$, $1$, $2$... $n$ mincí? Ako vieme z informácie, aké sumy idú zaplatiť pomocou prvých $k-1$, $k-2$ .. $1$, $0$ mincami vypočítať aké sumy idú zaplatiť $k$ mincami?

    int n, s;
    vector<int> mince(n);
    vector<vector<int> > tab(n+1, vector<int>(s+1, 1000000));

    tab[0][0] = 0;

    for(int i=0;i<n;++i)
    {
        for(int j=0;j<=s;++j) tab[i+1][j] = tab[i][j];

        for(int j=0;j<=s;++j) if(j+mince[i] <= s)
        {
            tab[i+1][j+mince[i]] = min(tab[i+1][j+mince[i]], tab[i][j]+1);
        }
    }

    cout << tab[n][s] << endl;