Prerekvizity na čítanie tohto textu: od čitateľa očakávame, že už aspoň videl haldu a binárny vyhľadávací strom a že by vedel implementovať vyhľadávanie v už existujúcom binárnom strome.
O potrebe vyvažovaných stromov
Na obrázku 1 sú štyri rôzne binárne vyhľadávacie stromy (binary search tree, BST). Všetky štyri obsahujú tú istú množinu prvkov, líšia sa však tvarom.
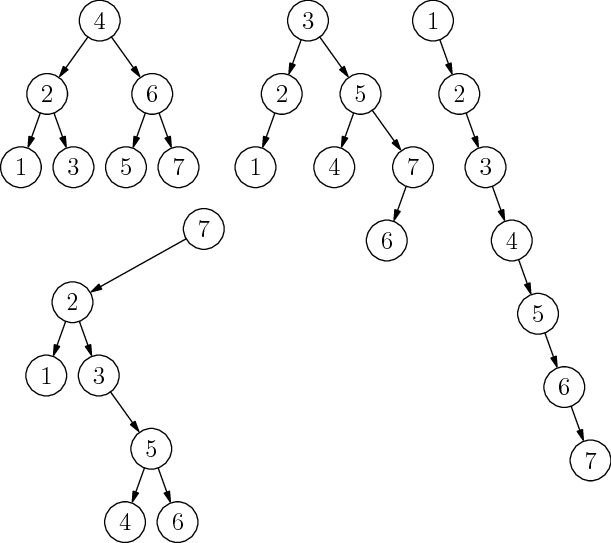
Pripomeňme si, že BST je zakorenený strom, v ktorom má každý vrchol nanajvýš jedného ľavého a nanajvýš jedného pravého syna. Navyše v každom vrchole platí podmienka BST: ľavý syn vrcholu $<$ vrchol $<$ pravý syn vrcholu.
Na tvare BST záleží. Čím je hlbší, tým dlhšie trvajú všetky operácie s ním: vyhľadávanie, vkladanie nového prvku, zmazanie existujúceho, atď. Samozrejme, tým, že ide o binárny strom, je jeho hĺbka zdola obmedzená: strom hĺbky $h$ môže mať nanajvýš $2^{h+1}-1$ vrcholov, a teda ak chceme strom s $n$ vrcholmi, musí jeho hĺbka byť aspoň logaritmická od $n$.
Existuje veľa rôznych spôsobov, ako zabezpečiť, že náš BST bude mať hĺbku $O(\log n)$, a teda že všetky operácie s ním budú rýchle. Najstaršia známa metóda je tá, ktorú používajú tzv. AVL-stromy. AVL-stromy sú BST, ktoré si v každom vrchole pamätajú "do ktorej strany sa nakláňa" a pomocou tejto informácie a šikovného robenia rotácií dosahujú, že strom je po každej operácii vyvážený (v nejakom špecifickom zmysle), z čoho potom vyplýva, že jeho hĺbka je určite logaritmická od počtu v ňom uložených prvkov.
V súčasnosti sa v praxi často používajú tzv. červeno-čierne stromy. Tie zabezpečujú "plytkosť" stromu pomocou inej techniky. Červeno-čierne stromy sú výbornou voľbou ak chceme vyrobiť robustnú knižnicu -- majú totiž aj zaručenú časovú zložitosť $O(\log n)$ na všetky operácie, aj celkom dobrú rýchlosť v praxi. A skutočne, keď si napríklad v g++ pozriete implementáciu dátových štruktúr set a map, stretnete v nej práve červeno-čierne stromy.
Červeno-čierne stromy však majú jednu značnú nevýhodu: zložitú a dlhú implementáciu plnú všelijakých rozborov prípadov. Občas sa nám stane, že sa ocitneme v situácii, v ktorej si potrebujeme rýchlo implementovať vlastný BST. Vtedy by sme v prvom rade uvítali to, aby zdrojový kód bol čo najstručnejší a s čo najmenej špeciálnymi prípadmi. A práve takúto dátovú štruktúru si teraz ukážeme.
QuickSort a náhoda
Hlavným trikom pri návrhu nášho stromu bude použitie náhody. Ale skôr, ako sa pozrieme na stromy, sa oplatí spomenúť si na triedenie QuickSort. To v skutočnosti veľmi úzko súvisí s binárnymi vyhľadávacími stromami. Pri triedení QuickSort vyberieme pivota a následne ostatné prvky v poli rozdelíme na dve kôpky: na tie menšie ako pivot a na tie väčšie ako pivot. Pri BST vyberieme prvok, ktorý bude v koreni, a následne ostatné prvky rozdelíme na dve kôpky: na menšie, ktoré idú do ľavého podstromu, a na väčšie od koreňa, ktoré idú do pravého podstromu.
Aj pri QuickSorte vieme, že najhorší možný prípad je zlý: keby sme napr. ako pivota vždy zvolili najmenší spomedzi usporadovaných prvkov, dostali by sme lineárnu hĺbku rekurzie (a z toho vyplývajúcu kvadratickú časovú zložitosť). Podobne je to u BST: ak dáme vždy do koreňa najmenší zo všetkých prvkov, dostaneme BST, ktorý bude vlastne len jedna dlhá cesta -- a teda budeme mať lineárnu hĺbku.
Pri QuickSorte si vieme pomôcť využitím náhody: dá sa dokázať, že ak pivota vždy volíme náhodne, tak takmer určite budeme mať len logaritmickú hĺbku rekurzie, a teda časovú zložitosť $O(n\log n)$. Intuícia za týmto tvrdením: aj keby sme vždy prvky rozdelili na povedzme 10% najmenších a 90% najväčších, dostali by sme strom rekurzie, ktorého všetky vetvy by mali len logaritmickú hĺbku. No a náhodne zvolený pivot nám pole aspoň takto dobre rozdelí s pravdepodobnosťou 80%.
Takéto niečo by sme chceli aj od nášho binárneho stromu: zoberieme naše prvky, nejak náhodne ich do stromu rozmiestnime a takmer určite dostaneme strom s logaritmickou hĺbkou.
No, sen je to pekný, ale so stromami je to predsa len o čosi ťažšie. Zatiaľ čo QuickSort je algoritmus, ktorý raz zbehne a je hotovo, strom potrebujeme dlhodobo udržiavať. Nestačí, keď bude v nejakom okamihu náhodne vyrobený. Potrebujeme, aby "prežil": aj keď doň postupne miliónkrát pridáme prvok, stále by sme chceli mať strom, ktorý bude v nejakom zmysle náhodný. Ako vieme takéto niečo dosiahnuť? Na scénu prichádza treap.
Treap
Na to, aby sme vrcholy v strome rozmiestnili náhodne, použijeme jednoduchý trik. Záznamy, ktoré budeme do stromu ukladať, budú mať dve zložky: kľúč a prioritu.
Kľúč je hodnota, ktorú sme tam mali aj doteraz -- teda to, podľa čoho prvky v strome usporadúvame, vyhľadávame, atď. Priorita je nový údaj, pomocou ktorého si náhodne zvolíme tvar stromu. V tomto texte budeme ako priority používať náhodné reálne čísla z intervalu od 0 po 1 a budeme ticho predpokladať, že žiadne dva prvky v strome nemajú presne rovnakú prioritu.
Keď si nižšie budeme ukazovať obrázky treapov, budeme v každom vrchole udávať usporiadanú dvojicu (kľúč,priorita). Nezabudnite však na to, že sa tam môžu okrem nich nachádzať aj iné údaje. Môžeme napríklad mať treap, ktorý má v každom vrchole uložený záznam o jednom riešiteľovi KSP, pričom ako kľúč používame jeho login. Takéto údaje však kvôli lepšej prehľadnosti v obrázkoch vynecháme.
Ako nám pomôžu priority náhodne určiť tvar nášho stromu?
Už vieme jednu vlastnosť, ktorú budeme od treapu požadovať: musí to stále byť BST. Presnejšie, keď sa budeme pozerať len na kľúče, musíme vidieť obyčajný BST. Druhá vlastnosť bude veľmi podobná, aj keď vás možno prekvapí: keď sa budeme pozerať len na priority prvkov, musíme vidieť binárnu haldu. V každom vrchole teda musí platiť, že jeho priorita je väčšia ako priorita každého z jeho synov.
Odtiaľ pochádza aj samotný názov našej dátovej štruktúry: slovo "treap" je kombináciou slov "tree" a "heap".
Existencia treapov
Počkať, počkať. Halda? Čo už je len toto za výmysel? Dá sa to vôbec dodržať? Čo ak máme zrovna také priority, pre ktoré to nejde?
Začnime tým, že sa na jeden treap pozrieme. Na obrázku si môžeme overiť, že všetky kľúče (prvé údaje) naozaj spĺňajú podmienku BST a všetky priority (druhé údaje) spĺňajú podmienku haldy.
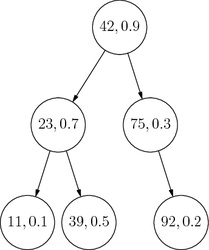
Čo to vlastne znamená, že priority spĺňajú podmienku haldy? Znamená to v prvom rade to, že prvok s najväčšou prioritou je určite v koreni celého stromu. Ak by pred nás niekto vysypal kopu prvkov (každý s nejakým kľúčom a nejakou prioritou), už vieme, čo by sme spravili v prvom kroku: našli by sme ten s najväčšou prioritou a dali by sme ho do koreňa.
Čo vieme povedať ďalej? Keďže kľúče majú tvoriť BST, akonáhle vieme, čo máme v koreni, tak je jednoznačne určené, ktoré prvky patria do ľavého podstromu a ktoré do pravého.
No a v každom podstrome môžeme teraz celú úvahu opakovať. Napríklad koreňom ľavého podstromu sa stane ten spomedzi prvkov v ňom, ktorý má spomedzi tých prvkov najväčšiu prioritu. A tak ďalej, až kým nevyrobíme celý treap.
Z vyššie uvedeného postupu vyplýva dôležité tvrdenie: Pre ľubovoľnú sadu dvojíc (kľúč,priorita) existuje presne jeden platný treap.
Na toto tvrdenie sa môžeme dívať nasledovne: tým, že sme každému prvku vygenerovali náhodnú prioritu, sme si vlastne náhodne zvolili tvar nášho stromu. A ako dobrá je táto náhodná voľba? Aby sme získali nejakú intuíciu, vráťme sa v myšlienkach ku našej analógii s QuickSortom. V našom strome sa deje niečo veľmi podobné. V každom podstrome treapu totiž platí, že každý prvok, ktorý sa doň dostal, mal rovnakú pravdepodobnosť toho, že práve on bude v tom podstrome koreňom. Najlepšie to je vidieť v koreni celého stromu: každý z našich $n$ prvkov mal na začiatku pravdepodobnosť $1/n$, že zrovna on dostane najväčšiu prioritu. Tým, že sme prvkom priradili náhodné priority, sme si teda koreň nášho treapu vybrali rovnomerne náhodne.
Zhrnutie
Zhrňme si, čo zatiaľ o treapoch vieme:
- Treap je binárny strom, do ktorého ukladáme dvojice (kľúč, priorita).
- Kľúče (a k ním priradené ďalšie dáta) sú tie údaje, ktoré nás naozaj zaujímajú.
- Ak sa pozeráme len na kľúče, vidíme obyčajný BST.
- Ak sa pozeráme len na priority, vidíme haldu.
- Kľúčmi a prioritami sú jednoznačne určené tvar treapu aj rozmiestnenie prvkov v ňom.
- Tým, že priority volíme náhodne, si vlastne implicitne náhodne zvolíme tvar stromu.
- Autori treapu už za nás poriadne dokázali, že skoro vždy bude hĺbka treapu logaritmická od počtu prvkov v ňom.
Treapy teda môžeme používať ako efektívnu implementáciu BST. O chvíľu si ukážeme, ako ich implementovať šikovne a veľmi, veľmi stručne.
Implementácia treapov
Treapy budeme implementovať podobne ako každý iný strom. V tomto texte si ukážeme ich implementáciu v C++. Začneme tým, že si vyrobíme štruktúru predstavujúcu jeden vrchol stromu. Tá môže vyzerať napríklad nasledovne:
struct item {
// kľúč je nejakého konkrétneho typu T
T key;
// priorita je celé číslo, lebo je zbytočné z rand() vyrábať číslo reálne
int priority;
// pointre na ľavého a pravého syna
item *l, *r;
// a ešte konštruktor, ktorý k danému kľúču priradí náhodnú prioritu
item(const T &key) : key(key), priority(rand()), l(NULL), r(NULL) {}
};
// pointer na item si nazveme pitem, nech je v neskoršom kóde menej *
typedef item* pitem;Vyhľadávať v treapoch sa dá rovnako ako v klasickom BST, tam nie je čo zlepšovať. Chceli by sme ale vedieť robiť operácie insert a erase: teda vkladať a vyberať prvky. Ako na to? Dalo by sa to robiť aj priamo, ale takáto implementácia je zbytočne zložitá. My na to pôjdeme "od lesa": ukážeme si dve iné operácie, ktoré sa obe implementujú veľmi ľahko, a potom si insert aj delete vyrobíme v podstate zadarmo.
Prvou operáciou bude split.
Split je jednoduchá operácia. Na vstupe dostane dve veci: treap $T$, uložený niekde v pamäti, a hodnotu kľúča $x$. Táto operácia prerobí treap $T$ na dva treapy $T_1$ a $T_2$. V treape $T_1$ skončia tie prvky $T$, ktoré majú kľúč menší alebo rovný $x$, v treape $T_2$ skončia všetky ostatné prvky. Dôležité je, že táto operácia zničí pôvodný treap $T$. Nič sa teda nikam nekopíruje, len presmerujeme niektoré pointre medzi vrcholmi tak, aby sa pôvodný treap rozpadol na dva menšie.
Ako spraviť split? Začneme v koreni. Ak ten patrí (podľa svojho kľúča) do $T_1$, tak aj celý ľavý podstrom patrí do $T_1$. Rekurzívne teda zavoláme split na pravý podstrom. Ten sa nám rozpadne na dve časti: ľavú, ktorá ešte patrí do $T_1$, a pravú, ktorou je celé $T_2$. Už len teda ľavú časť, ktorú nám vrátilo rekurzívne volanie, zavesíme pod koreň $T_1$ ako jeho pravý podstrom a sme hotoví. No a ak koreň patrí už do T2, tak spravíme to isté, len v jeho ľavom podstrome.
Tu je celá implementácia:
// split:
// -- v premenných t, key dostane vstup
// -- do premenných l, r vyplní výstup, teda pointre na korene treapov T1 a T2
void split(pitem t, T key, pitem &l, pitem &r) {
if (!t) { l = r = NULL; return; }
if (key < t->key) {
split(t->l, key, l, t->l);
r = t;
} else {
split(t->r, key, t->r, r);
l = t;
}
}Druhou operáciou bude merge. Tú si je najlepšie zapamätať ako "undo split". Vstupom pre merge sú teda dva treapy $T_1$ a $T_2$. Ale nie len tak hocijaké: musí platiť, že každý kľúč v $T_1$ je menší ako každý kľúč v $T_2$. (Inými slovami, platným vstupom pre merge je výstup splitu.) Operácia merge v pamäti prehádže pointre tak, aby tieto dva menšie treapy spojila do jedného.
Ako spraviť merge? Začneme tým, že sa pozrieme na korene oboch menších treapov. Ten z nich, ktorý má väčšiu prioritu, bude zjavne koreňom výsledného treapu. Čo sa stane, ak je to koreň treapu $T_1$? Jeho ľavý podstrom ostane nedotknutý. A jeho nový pravý podstrom vznikne tak, že mergneme dokopy jeho súčasný pravý podstrom a celý treap $T_2$. (V tomto kroku sme využili pozorovanie, že všetky kľúče v $T_2$ sú väčšie ako kľúč z koreňa $T_1$, a teda celý $T_2$ patrí do jeho pravého podstromu.) No a ak celkovým koreňom bude pôvodný koreň $T_2$, stane sa to isté, len symetricky.
Celá implementácia tejto myšlienky má opäť len pár riadkov:
// merge:
// -- v premenných l, r dostane vstup
// -- do premennej t vyplní výstup, teda pointer na koreň spojeného treapu
void merge(pitem &t, pitem l, pitem r) {
if (!l || !r) {
t = l ? l : r;
return;
}
if (l->priority > r->priority) {
merge(l->r, l->r, r);
t = l;
} else {
merge(r->l, l, r->l);
t = r;
}
}No dobre. Vieme split a merge. My sme ale chceli robiť insert a delete! Ako na ne?
Insert sa teraz spraví ľahko. Máme treap a dostali sme nový prvok, ktorý doň chceme vložiť. (Pre jednoduchosť predpokladajme, že sa prvok s týmto kľúčom ešte v treape nenachádza. Ak potrebujeme zahadzovať duplikáty, spravili by sme najskôr kontrolu, či tento prvok už v treape máme.)
Začneme v koreni treapu. Opäť sú len dve možnosti. Prvou je, že náš nový prvok má prioritu menšiu ako koreň treapu. V takomto prípade porovnáme ich kľúče, aby sme zistili, či náš prvok patrí do ľavého alebo pravého podstromu. A keď to už vieme, tak ho do príslušného podstromu vložíme rekurzívnym volaním funkcie insert.
Druhou možnosťou je, že náš nový prvok má od aktuálneho väčšiu prioritu. Čo vtedy? Nuž, vtedy sa má náš nový prvok stať koreňom. Zavoláme teda na náš pôvodný treap funkciu split, pričom ako kľúč použijeme kľúč práve vkladaného prvku. Dostaneme tak treapy $T_1$ a $T_2$. Náš nový prvok bude koreňom treapu a treapy $T_1$ a $T_2$ budú jeho ľavým a pravým podstromom.
Vo všeobecnosti sa teda stane to, že začneme v koreni a podľa kľúča spravíme niekoľko krokov dodola, až kým sa nedostaneme na miesto, kam už náš vkladaný prvok podľa priority patrí. V tej chvíli zavoláme split, príslušný podstrom rozbijeme na dva menšie kusy a medzi ne vložíme ten nový prvok.
Implementácia je opäť veľmi stručná:
void insert(pitem &t, pitem it) {
if (!t) {
t = it;
return;
}
if (it->priority > t->priority) {
split(t, it->key, it->l, it->r);
t = it;
} else {
insert(it->key < t->key ? t->l : t->r, it);
}
}A ako sa prvky maže? Ešte ľahšie.
Ak je prvok, ktorý chceme zmazať, priamo v koreni, tak ho zmažeme, zavoláme merge na jeho podstromy a máme hotovo. A ak nie je v koreni, tak sa len rekurzívne zavoláme na podstrom, v ktorom sa (podľa kľúča) nachádza.
void erase(pitem &t, T key) {
if (!t) return;
if (t->key == key) merge(t, t->l, t->r);
else erase(key < t->key ? t->l : t->r, key);
}Tak, a to je všetko. Tieto štyri stručné metódy už dokopy tvoria plnohodnotný vyvažovaný binárny vyhľadávací strom.
Pridávanie ďalších fičúrií
Tu samozrejme naša cesta nekončí. Keby sme len chceli usporiadanú množinu, mohli sme použiť štandardný knižničný set a mali by sme to bez práce. My ale vlastné stromy implementujeme práve preto, aby sme do nich mohli dorobiť funkcionalitu, ktorú nám štandardné knižnice neponúkajú.
Jednou často užitočnou fičúriou je prístup ku k-temu najmenšiemu prvku. Chceli by sme teda vedieť pre ľubovoľné $k$ vedieť v logaritmickom čase odpovedať na otázku: "keby sme všetky prvky z tohto stromu mali v usporiadanom poli, ktorý prvok by bol na indexe $k$?"
Takéto niečo vieme veľmi ľahko implementovať. Jediné, čo treba spraviť, je do každého vrcholu pridať premennú, v ktorej si pamätáme veľkosť podstromu, ktorého je koreňom. (Inými slovami, keby sme odstrihli hranu z tohto vrcholu do jeho otca, koľko vrcholov by odpadlo?)
Toto sa robí ľahko. Stačí vždy, keď nejaký vrchol meníme, prepočítať túto hodnotu z hodnôt jeho synov: veľkosť môjho podstromu je 1 (za mňa), plus veľkosť podstromu môjho ľavého syna (ak nejakého mám), plus veľkosť podstromu môjho pravého syna (detto).
Celá implementácia je teda len pár riadkov navyše. Začneme tým, že si vyrobíme dve pomocné funkcie:
int get_size(pitem t) { return t ? t->size : 0; }
void update(pitem t) { if (t) t->size = 1 + get_size(t->l) + get_size(t->r); }No a teraz už len stačí pridať volanie update(t) na koniec každej z funkcií split, merge, insert a erase a máme strom, ktorý si správne udržiava veľkosti podstromov.
Akonáhle máme túto pomocnú informáciu, vieme v logaritmickom čase "indexovať" do nášho treapu. Predstavme si, že sme v koreni treapu a hľadáme prvok na indexe $k$. Pozrieme sa na size pre ľavého syna koreňa a dozvieme sa, že je $x$. Čo to znamená? Znamená to, že prvky na indexoch 0 až $x-1$ sú v ľavom podstrome koreňa, na indexe $x$ je koreň, a od indexu $x+1$ začínajú prvky v pravom podstrome koreňa. Podľa porovnania $k$ a $x$ vieme, kde želaný prvok hľadať (a ak ho
hľadáme v pravom podstrome, vieme, že v rámci neho chceme prvok s indexom $k-x-1$).
Implementácia:
T operator[](int x) { return kth_smallest(root,x); }
T kth_smallest(pitem p, int x) {
int l = get_size(p->l);
return l > x ? kth_smallest(p->l,x) : l == x ? p->key : kth_smallest(p->r,x-l-1);
}Treapy s implicitnými kľúčami
Na záver si ešte ukážeme jeden trik, ktorý sa dá pomocou treapov robiť. Vieme si pomocou nich vyrobiť dátovú štruktúru, ktorá sa bude podobať na obyčajné pole. Prístup ku konkrétnemu prvku, teda operátor [], bude potrebovať až logaritmický čas. Zato ale budeme vedieť efektívne robiť omnoho viac operácií ako s obyčajným poľom:
- vieme v logaritmickom čase pridať nový prvok kamkoľvek do poľa (na začiatok, koniec, aj medzi ľubovoľné dva prvky)
- vieme v logaritmickom čase odstrániť ľubovoľný prvok z poľa
- dá sa dorobiť veľa ďalšieho, ako napríklad nájdenie minima ľubovoľného úseku, "ofarbenie" ľubovoľného úseku, či dokonca reverz ľubovoľného úseku, v logaritmickom čase
Hlavná myšlienka bude nasledovná: Budeme mať dáta, teda v každom vrchole stromu bude uložený údaj, ktorý by bol uložený na jednom políčku obyčajného poľa. Budeme mať aj priority, používané budú presne rovnako ako vo vyššie popísanej implementácii. Vôbec však nebudeme mať kľúče. Namiesto toho sa budeme tváriť, že pre každý prvok platí, že jeho aktuálnym kľúčom je index, na ktorom by ležal v usporiadanom poli. (Inými slovami, jeho index v in-order zápise aktuálneho treapu.)
Kľúče si nikdy nebudeme nikam ukladať. To by ani nefungovalo -- akonáhle by sme pridali nejaký nový prvok do stredu, museli by sme prečíslovať všetky vrcholy napravo od neho. Namiesto toho si kľúče budeme priebežne počítať počas operácií s treapom.
Toto počítanie bude veľmi jednoduché. Keď sme v koreni, vieme, že jeho aktuálny kľúč je rovný počtu vrcholov v jeho ľavom podstrome. A ako schádzame dole stromom, vieme si priebežne pamätať, koľko existuje v našom treape vrcholov menších od aktuálneho, a teda od akého kľúča začínajú prvky v jeho podstrome. Inými slovami, robíme presne to isté, ako vo vyššie popísanej metóde kth_smallest.
Metóda merge sa vôbec nezmení, keďže tá sa na kľúče nepotrebovala pozerať. Ukážeme si teraz novú implementáciu metódy split.
// pribudol parameter add hovoriaci, že prvky v podstrome s koreňom t začínajú od indexu add
void split(pitem t, T key, pitem &l, pitem &r, int add = 0) {
if (!t) { l = r = NULL; return; }
int t_key = add + get_size(t->l); // vypočítame implicitne určený kľúč pre vrchol t
if (key < t->key) {
split(t->l, key, l, t->l, add);
r = t;
} else {
split(t->r, key, t->r, r, add + 1 + get_size(t->l));
l = t;
}
}Vloženie nového prvku sa dá spraviť tak, že na vhodnom mieste spravíme split aktuálneho treapu na $T_1$ obsahujúci prvky, ktoré majú byť naľavo od vkladaného a $T_2$ obsahujúci prvky, ktoré majú byť napravo od neho. Potom spravíme jednoprvkový $T_3$ obsahujúci vkladaný prvok a spravíme merge(merge(T1,T3),T2).
Vymazanie prvku je ešte ľahšie. Nájdeme prvok, ktorý chceme vymazať, zmažeme ho a "dieru po ňom" zaplátame jednoducho tak, že spravíme merge jeho oboch podstromov.
Operácie na intervaloch sa robia tak, že v každom vrchole pribudnú nové premenné, obsahujúce informáciu o jeho podstrome. Vždy, keď vrchol navštívime a nejak zmeníme, vieme túto informáciu prepočítať z jeho synov. (Napr. minimum pre môj podstrom viem určiť z miním pre podstromy mojich synov a z hodnoty, ktorá je v mojom vrchole.) Operácie potom robíme tak, že pomocou dvoch splitov odizolujeme interval, ktorý nás zaujíma, pozrieme sa do jeho koreňa (resp. tam niečo zapíšeme) a následne všetko mergeneme naspäť do jedného stromu.
Čas poslednej úpravy: 10. január 2017 22:14